Для формирования контура управления высотой полета не­обходимо измерять сигнал высоты с помощью, например, баро­метрического высотомера, сигнал скорости изменения высоты, получаемый путем дифференцирования сигнала высоты, сигнал угла тангажа, который необходим для демпфирования движения центра масс и сигнал угловой скорости тангажа, необходимый для демпфирования угловых движений. Представленная на рис. 14 схема отражает указанную структуру сигналов.

Рис. 14. Структурная схема системы управления высотой полета

  Рассмотрим работу схемы при отклонении высоты полета от заданной, например, при наборе высоты (рис. 15).

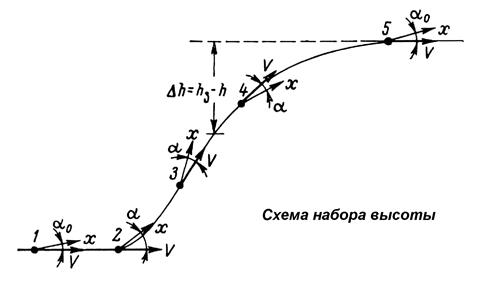
Рис. 15. Схема набора высоты.

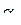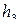В горизон­тальном установившемся полете (точка 1) между вектором ско­рости V и продольной осью ЛА х имеется положительный угол атаки . Пусть в точке 2 с помощью ручки управления автопи­лотом создано рассогласование  (где  и h — соответ­ственно заданная и фактическая относительные высоты полета), под действием которого произойдет отклонение руля высоты и продольной оси х кверху, при этом угол атаки получит прира­щение 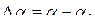, что приведет к увеличению подъемной силы. Вследствие этого вектор скорости начнет поворачиваться вверх и траектория полета искривится. В точке 3 уменьшается рассогласование  и возрастает сигнал угла тангажа, что приведет к уменьшению угла отклонения руля высоты. При этом уменьшится угол атаки и приращение подъемной силы, поэтому вектор скорости перестает поворачиваться. Между точками 3 и 4 име­ется такая точка, в которой сигнал рассогласования стано­вится равным сигналу угла тангажа, поэтому руль высоты зай­мет нейтральное положение, а угол атаки станет равным значе­нию 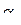 которое было в горизонтальном полете. При дальнейшем наборе высоты сигнал  продолжает уменьшаться, поэтому под действием сигнала угла тангажа руль будет отклонен вниз, а угол атаки станет отрицательным (точка 4). Траектория поле­та будет искривляться выпуклостью вверх, пока ЛА не перейдет в точке 5 в горизонтальный полет. Теперь угол атаки опять будет равен 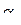. Из изложенного видно, что при автоматическом управлении высотой полета ЛА совершает сложное движение в вертикаль­ной плоскости.

    Рассмотрим процессы управления высотой полета ЛА с по­мощью статического автопилота (см. рис. 14). Закон управле­ния автопилота, как видно из схемы, имеет вид

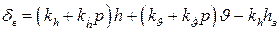              (76)

  В дальнейшем будем полагать, что элементы системы управ­ления не имеют динамических погрешностей. Такое предположе­ние реализуется легко, поскольку движение центра масс является медленным. Возьмем уравнение ЛА в виде (18), полагая скорость полета постоянной. Исключая из уравнений (18) и (76) переменную 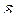, получим

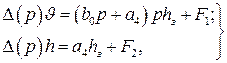                              (77)

       где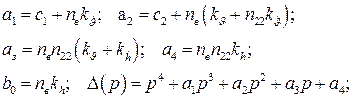              

    а величины 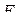 и 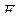 — внешние возмущения, вызванные фактора­ми ,  и 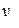 [см. уравнения (18)].

Устойчивость системы (77) следует из неравенства

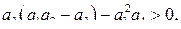                             (78)

а критический коэффициент усиления 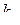 будет

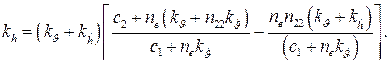                 (79)

     Из выражения (79) видно, что для увеличения коэффициен­та 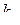 необходимо увели-чивать коэффициенты ,  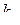и . Следует заметить, что управлять высотой полета без сигналов угла и угловой скорости тангажа невозможно. Это, в частности, следует из выражения (79), если в нем положить 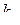 и =0. При этом сигнал угловой скорости необходим для демпфирования уг­ловых движений, а сигнал угла — для демпфирования движений центра масс.

Передаточные числа системы управления высотой полета бу­дем выбирать из условий получения заданного переходного про­цесса. Для этого потребуем, чтобы передаточная функция по управляющему сигналу

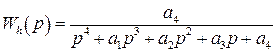                             (80)

совпадала с передаточной функцией

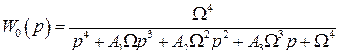                (81)

где , ,  и  -заданные величины.

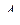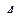Из сравнения коэффициентов передаточных функций (80) и (81) получаем выражения для коэффициентов передачи

(82)

    Передаточные числа 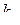 и  имеют тот же порядок величин, что и значения, полу-ченные при исследовании угловых движений. Это обстоятельство позволяет пользо-ваться одними и теми же передаточными числами как при управлении угловыми движениями, так и при управлении дви­жением центра масс.

   Отметим, что из кинематического соотношения 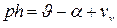, следует, что угол тангажа с точностью до  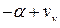совпадает с производной от сигнала высоты. Поэтому в продольных каналах автопилотов сигнал  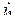почти никогда не используется, а соответствующее демпфирование движений центра масс достигается за счет сигнала угла тангажа.

  При использовании астатического автопилота для управления высотой полета закон управления обычно имеет вид

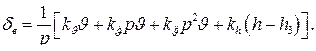                   (83)

Однако такие автопилоты, не имеют преимуществ перед статическим автопилотом.

Лекция 16.

План

1. Управление высотой полета низколетящих самолетов.

2. Управление боковым движением центра масс самолета.