Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

  Значительный класс задач, выполняемых ЛА, сводится к обеспечению встречи с целью. Под целью будем понимать точ­ку пространства (на земле или в воздухе), являющуюся конеч­ной точкой траектории полета ЛА. В качестве ЛА будем рас­сматривать самолет, наводимый на воздушную или наземную цель, или ракету, запускаемую с самолета или с земли и наводи­мую на ту же цель. Цель может совершать произвольное дви­жение или оставаться неподвижной.

     Характер встречи ЛА с целью может быть различным. При мягкой контактной встрече ЛА должен оставаться невредимым. При ударной контактной встрече ЛА разрушается, но при этом уничтожается и цель. Наконец, при бесконтактной встрече воз­действие ЛА на цель осуществляется путем стрельбы, бомбоме­тания, пуска ракет, фотографирования и т. д.

   Во всех случаях встреча ЛА с целью должна быть достаточ­но точной. Неточности возникают из-за погрешностей систем наведения и управления, маневрирования цели или организован­ного противодействия.

  При организации встречи ЛА с целью приходится решать ряд задач, которые сводятся к получению информации о движе­нии цели и ЛА, передаче информации на пункты управления и ее переработке, формированию команд управления, наведению и самонаведению ЛА аппарата и др.

    На рис. 20 показана функциональная схема системы наведе­ния. Полученная информация о цели вместе с информацией о движении ЛА обрабатывается и на ее основе вырабатываются команды управления, которые используются для организации способов движения ЛА по направлению к цели (методы наведе­ния). Эти команды отрабатываются системой управления (кон­тур управления).

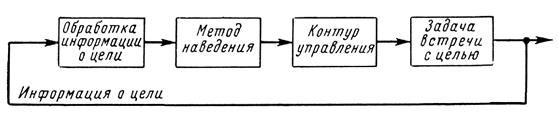
Рис.20. Функциональная схема системы наведения.

       Системы автоматического управления при наведении на цели могут быть автономными и неавтономными. В автономных си­стемах отсутствуют текущая информация о цели, а программа управления вводится до старта. В полете производится сравне­ние текущих значений параметров движения с программными значениями и на этой основе вырабатываются управляющие сигналы. Автономные системы применяются при наведении на неподвижные цели или цели, движение которых достаточно точ­но можно предсказать. Для наведения на подвижные цели при­меняются неавтономные системы, поскольку необходимая для управления информация может быть получена за счет информа­ционной связи с наземными станциями наведения или целью. К таким системам относятся системы телеуправления, самонаве­ дения и комбинированные системы.

       Системы телеуправления, в свою очередь, делятся на системы наведения по лучу, командные системы и радионавигационные системы. В системах телеуправления информация о координатах ЛА и цели получается на пункте наведения, где производится формирование управляющих сигналов, передаваемых по линии телеуправления на борт ЛА. В частности, в системах наведения по лучу измерение отклонения ЛА от равносигнальной зоны луча и формирование управляющих сигналов производится на ЛА, а наведение луча на цель осуществляется с пункта наведения. Системы самонаведения характеризуются тем, что информация о координатах цели получается на борту летательного аппарата. Здесь же формируются управляющие сигналы.

Наведение ЛА на цель нередко состоит из двух этапов: даль­него наведения, осуществляемого посредством автономных си­стем или систем телеуправления, и ближнего наведения, реали­зуемого системами самонаведения.

Лекция 19.

План

1. Понятие о методе наведения ЛА на цель.

2. Основные кинематические уравнения методов на­ведения.

 

5.2. Методы наведения. Основные кинематические уравнения методов на­ведения.

   Способ организации движения ЛА для встречи с целью назы­вается методом наведения. Метод наведения по существу явля­ется желаемым законом изменения углового положения вектора скорости ЛА при сближении с целью.

    Известны различные методы: прямого наведения, погони, преследования с упреждением, пропорционального сближения, параллельного сближения и накрытия цели. Наведение ЛА на цель совершается в горизонтальной и вертикальной плоскостях, т. е. по двум каналам наведения. В качестве характеристик метода наведения, определяющего идеальные траектории полета ЛА, выбирают время полета, мак­симальную угловую скорость линии визирования, максимальное нормальное ускорение и полосу частот, необходимую для реали­зации управления.

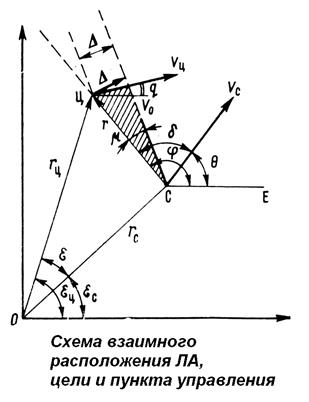
Рис.21.

   Для пояснения существа мето­дов наведения обратимся к рис. 21, на котором дано взаим­ное расположение цели Ц, лета­тельного аппарата С и пункта наведения О.

Векторы скоростей ЛА и цели обозначим через V_c и V_ц. Радиусы-векторы r_с и r_ц определяют положения ЛА и цели по отношению к пункту наведе­ния О, а радиус-вектор r и отно­сительная скорость V₀ = V_C - V_ц характеризуют взаимное положе­ние и движение ЛА и цели. Обозначим также: 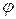 — угол между линией СЕ (линией горизонта) и радиусом-вектором r;  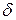—угол между радиусом-вектором r и вектором скорости летательного аппарата V_c, называемый углом упреждения;  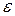— угол между радиусами-векторами r_с и r_ц;  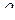—угол между вектором V_c и ли­нией СЕ;  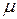—угол между векторами r и V₀;  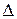—мгновенный промах. Метод наведения в значительной мере определяет точность наведения на цель, характеризуемую промахом.

Мгновенным промахом называется минимальное расстояние 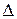, на котором пройдет ЛА от цели, если, начиная с данного мо­мента времени, ЛА и цель будут двигаться равномерно и прямо­линейно с теми скоростями, которые они имеют в рассматривае­мый момент времени, или будут двигаться с одинаковыми уско­рениями.

Мгновенный промах является векторной величиной 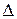, при­чем, поскольку модуль этого вектора 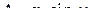, то                                     

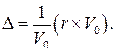                                    (99)

  Если учесть, что 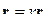, где — единичный вектор относи­тельной дальности и 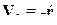, тогда

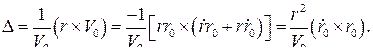
Но 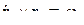 —угловая скорость линии визирования ЛА — цель, поэтому

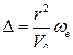                                 (100)

  Отсюда следует, что при прочих равных условиях промах тем больше, чем больше угловая скорость линии визирования.

  Выразим производную от промаха 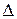 через ускорения ЛА j_c и цели j_ц Для этого из выражения (99) находим

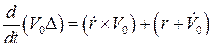
 или, пользуясь тем, что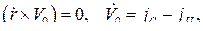   

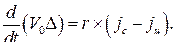                       (101)

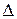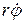Отсюда следует, что для изменения промаха  необходимо управлять ускорением ЛА j_c. Ускорение цели j_u является воз­мущающим фактором. Для получения уравнений методов наведения выразим составляющие  и  вектора относительной скорости  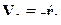через проекции скорости цели V _ц и ЛА V_c на направление ра­диуса-вектора  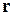(см. рис.21). Находим:

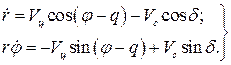                     (102)

  Это и есть основные кинематические уравнения методов на­ведения в вертикальной плоскости. Аналогичные уравнения по­лучаются для наведения в горизонтальной плоскости.

Для получения характеристик различных методов наведения необходимо к уравнениям (102) добавить дополнительные соот­ношения, свойственные этим методам. В дальнейшем в этом раз­деле будем рассматривать случай горизонтального движения це­ли, при котором .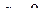

Лекция 20.

План

1. Метод погони.

2. Метод прямого на­ведения.

3. Метод преследования с упреждением.

Метод погони.

Если угол упреждения равен нулю:

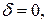                                        (103)

т. е. вектор скорости ЛА V_c все время направлен на цель, то получаем метод наведения, называемый методом погони. Для этого метода из уравнений (101) получаем:

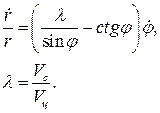                                 (104)

Если 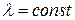, то интегрирование уравнения (104) при на­чальных условиях  позволяет получить кинема­тические траектории соответственно для удаляющейся и прибли­жающейся цели:

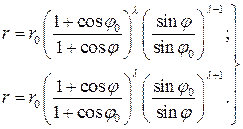                  (105)

  Время полета ЛА к цели может быть найдено, например, путем интегрирования второго уравнения (102), из которого по­лучаем

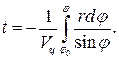
Воспользовавшись выражением (105), найдем время для удаляющейся и приближающейся цели:

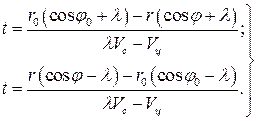              (106)

  Для получения времени встречи ЛА с целью следует поло­жить 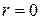, тогда

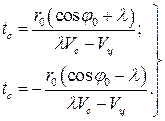                       (107)

   Из этих выражений видно, что удаляющуюся цель можно перехватить только при 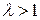, т. е. когда скорость ЛА больше скорости цели. Для приближающейся цели перехват возможен как при 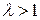, так и при .

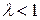   На рис. 22 построены траектории полета (кривые погони) цели и ЛА для удаляющейся цели (рис. 22, а) и для приближающейся цели (рис. 22,6). При построении предполагалось, что время встречи t_c раз­делено на равные промежутки  и в течение каждого проме­жутка  скорости цели и ЛА постоянны.

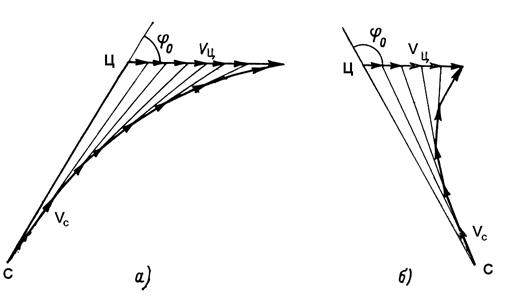
Рис. 22. Траектории полета при наведении по методу погони

  Угловая скорость линии визирования в методе погони может быть найдена из второго уравнения (102) и уравнения (105):

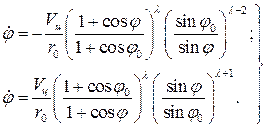              (108)

   Легко видеть, что встреча с приближающейся целью будет при 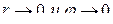, а с удаляющейся целью — при .

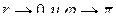Нормальное ускорение ЛА в методе погони будет

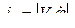                                 (109)

   Очевидно, что при 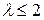 нормальное ускорение в момент встречи конечно, а при 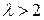— стремится к бесконечности.

5.4. Методы прямого на­ведения и преследования с упреждением.

    В некоторых случаях реализуется метод наведения, при ко­тором не вектор скорости, а продольная ось ЛА все время на­правлена на цель. Такой метод называется методом прямого на­ ведения. Поскольку направление продольной оси отличается от направления вектора скорости 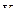 на углы атаки  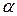и скольже­ния 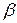, то характеристикой метода прямого наведения будет (в вертикальной плоскости)

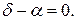                                  (110)

    Метод наведения, при котором угол между вектором скоро­сти ЛА и линией визирования «ЛА — цель» остается постоян­ным, называется методом преследования с упреждением. Харак­теристикой этого метода является

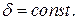                                  (111)

    Из уравнений (102) при условии (111) получаем уравнение с разделяющимися переменными

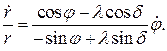                       (112)

  Интегрирование этого уравнения при 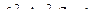, что имеет место в действительности, дает 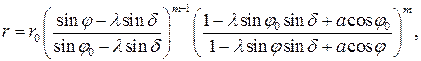(113):

      (113)

 

     где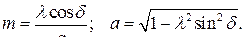                          

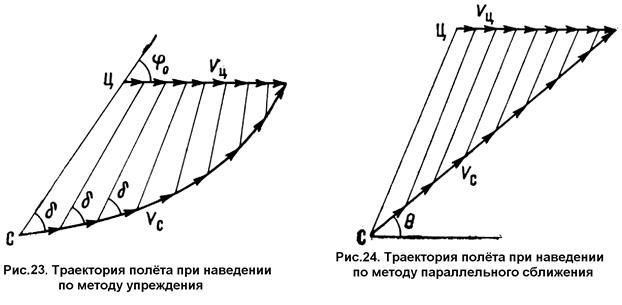
Представление о траекториях полета ЛА и цели дает графи­ческое построение при 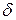 = const и 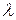=2, приведенное на рис. 23.

  Время полета ЛА может быть получено интегрированием первого уравнения системы (102) с учетом выражения (113):

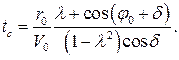                     (114)

  Для определения угловой скорости линий визирования в этом методе необходимо взять второе уравнение системы (102), подставив в него значение 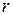 из выражения (113). На­ходим:

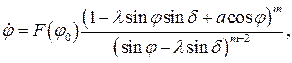          (115)

где F( 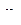) — имеет конечное значение.

Из выражения (115) видно, что угловая скорость 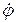 может быть бесконечно большой только при 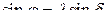. Нормальное ускорение в методе преследования с упрежде­нием находится по формуле (109), в которую необходимо под­ставить  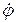из выражения (115)

 

Лекция 21.

План

1. Мето­д параллельного сближения.

2. Метод пропорционального сближения.

3. Метод накрытия цели.

 

5.5. Мето­д параллельного сближения.

 

    Метод наведения, при котором линия визирования «ЛА — цель» перемещается параллельно самой себе, называется мето­ дом параллельного сближения. Если цель движется прямоли­нейно, то, как видно из построения на рис. 24, траектория ЛА также прямая линия.

  Легко видеть, что при этом методе наведения 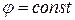 и  (см. рис. 21) или

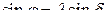                                    (116)

Кинематические соотношения для метода параллельного сближения при условиях 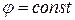и  получаются интегри­рованием уравнений (102):

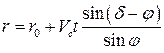                                 (117)

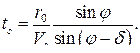                                   (118)

  Так как в рассматриваемом методе наведения угловая ско­рость линии визирования равна нулю, т. е. , то в соответст­вии с выражением (109) нормальное ускорение также равно нулю. Если цель движется по криволинейной траектории, то траектория ЛА также будет криволинейной, а ускорение 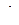 уже не будет равно нулю.

Для реализации метода параллельного сближения необходи­мо подавать в систему управления сигнал приращения угловой скорости линии визирования ЛА — цель. Этот сигнал возникает при отклонении вектора скорости V₀ от направления в точку встречи на угол 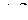, т. е.

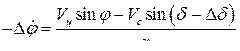
или вследствие малости 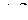 и использования уравнения (116)

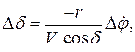                                  (119)