Скорость самолета в горизонтальном полете определяется из уравнения

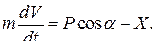                         (88)

  Сила тяги Р и сопротивление X зависят от скорости полета. В установившемся режиме полета сила тяги Р равна силе сопротивления X , т. е. Р = Х. Из этого равенства можно определить величину установившейся скорости полета. В неустановившемся движении величина ускорения dV / dt и ха­рактер ее изменения определяются видом функций P ( V ) и X ( V ).

  Самолет по отношению к скорости полета может быть устой­чивым или неустойчивым в зависимости от взаимного протека­ния характеристик P ( V ) и X ( V ) в точке их пересечения. Пола­гая, что скорость 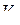 соответствует равенству Р = Х и беря линей­ные члены разложения функций P ( V ) и X ( V ) в ряды по малым приращениям 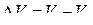, преобразуем уравнение (88)к виду

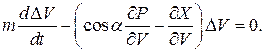                       (89)

   Если положить приближенно 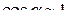, то условие устойчи­вости самолета по отношению к скорости полета примет вид

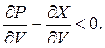                             (90)

    Необходимость управления скоростью полета возникает при сверхзвуковых полетах, а также при режимах за­хода на посадку, при наведении самолетов на цели, при полете в строю и др.

   Для управления скоростью полета можно воздействовать на тягу двигателя и на руль высоты. Изменение тяги двигателя достигается его дросселированием, что при наличии объединенного управления сводится к перемещению ручки управления. При воздействии на руль высоты меняется угол атаки, что ведет к изменению силы сопротивления.

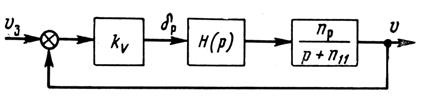
Рис. 18. Структурная схема статического регулирования скорости полета.

    Так как авиационный двигатель, используемый в качестве регулирующего фактора при управлении скоростью полета, фор­мирует требуемую тягу с запаздыванием по отношению к пере­мещению ручки управления, то его динамические характери­стики будут влиять на динамику контура управления скоростью полета. Поэтому при исследовании процессов в контуре управле­ния скоростью полета следует учитывать запаздывание в пере­даче сигналов через двигатель.

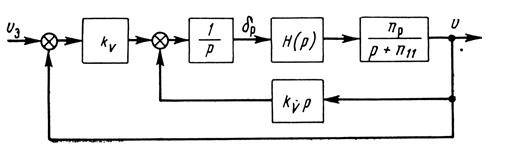
Рис. 19. Структурная схема астатического регулирования скорости полета.

   Для автоматического регулирования скорости полета могут быть применены статический и астатический регуляторы (рис. 18 и 19). В качестве чувствительных элементов в этих регуляторах обычно применяются аэрометрические измерители скорости полета, а сигналы ускорений могут быть получены с помощью акселерометров или дифференцирующих устройств. На этих схемах передаточная функция самолета по скорости полета отображена инерционным звеном, а передаточная функ­ция авиадвигателя — звеном 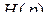, которое в дальнейшем тоже будем считать инерционным, т. 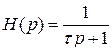е. , где 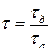, 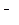-постоянная времени авиадвигателя.

   При рассмотрении динамики процессов управления ско­ростью полета будем полагать, что угловые движения самолета стабилизируются быстродействующим автопилотом. В таком случае математическая модель самолета как объекта управле­ния по скорости полета может быть представлена уравнением

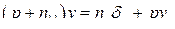                                 (91)

    где 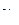 — продольные порывы ветра.

Уравнения движения автоматов скорости с учетом передаточ­ной функции авиадвигателя, как следует из схем (см. рис. 18 и 19), можно представить:

для статической

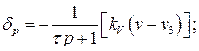                         (92)

для астатической системы

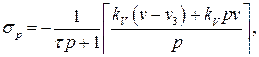                              (93)

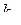    где  и 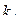—передаточные числа и  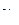— сигнал заданной ско­рости полета.

Рассмотрим переходные процессы в статическом автомате скорости полета, для чего решим совместно уравнения (91) и (92). Найдем уравнение замкнутой системы

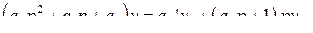              (94)

              где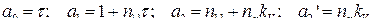          

Поскольку для неустойчивых по скорости полета самолетов 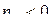, то условиями устойчивости системы будут:

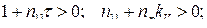                       (95)

  Первое условие всегда выполняется, поскольку 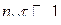. Для выполнения второго условия передаточное число  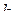должно удовлетворять условию

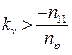                                            (96)

  В случае астатического автомата скорости полета, решая совместно уравнения (91) и (93), получаем

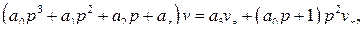              (97)

    где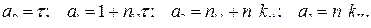          

Для устойчивости системы необходимо удовлетворить условиям:

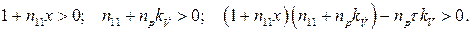        (98)

Отсюда следует, что если 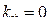, то система структурно неустойчива.

    Можно выбрать такие передаточные числа 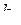 и 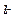, при ко­торых переходные процессы будут удовлетворительны. Однако, если учесть, что астатический автомат скорости полета более сложен, чем статический, а преимущества его незначительны, то в системах чаще применяют статические автоматы.