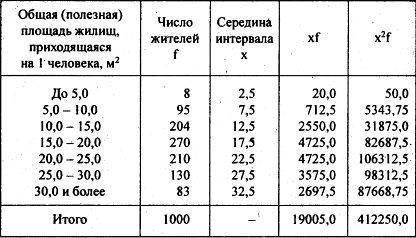
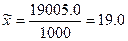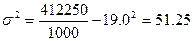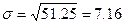;
;
.
Средняя ошибка выборки составит:
.
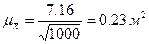Определим предельную ошибку выборки с вероятностью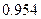 
:
.
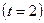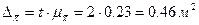Установим границы генеральной средней:
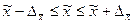или 
.
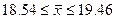Таким образом, на основании проведенного выборочного обследования с вероятностью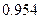 
можно заключить, что средний размер общей площади, приходящейся на одного человека, в целом по городу лежит в пределах от 
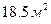до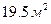 
.
При расчете средней ошибки собственно-случайной бесповторной выборки необходимо учитывать поправку на бесповторность отбора:
.
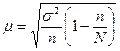Если предположить, что представленные в табл. 2.1 данные являются результатом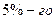 
бесповторного отбора (генеральная совокупность включает 
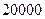единиц), то средняя ошибка выборки будет несколько меньше:
.
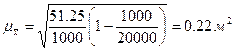Соответственно уменьшится и предельная ошибка выборки, что вызовет сужение границ генеральной средней.
Воспользуемся еще раз данными табл. 2.1 для того, чтобы определить границы доли лиц, обеспеченность жильем которых составляет менее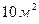 
.
Согласно результатам обследования, численность таких лиц составила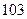 
человека.
Определим выборочную долю и дисперсию:
;
.
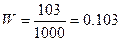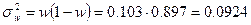Рассчитаем среднюю ошибку выборки:
.
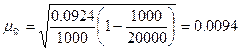Предельная ошибка выборки с заданной вероятностью составит:
.
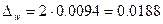Определим границы генеральной до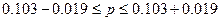ли:
или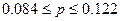 
.
Следовательно, с вероятностью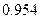 
можно утверждать, что доля лиц, имеющих менее 
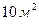на человека, в целом по городу находится в пределах от 
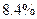до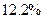 
.
Механическая выборка
Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.).
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.
Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы. Например, при пропорции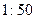 
( 
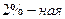выборка) отбирается каждая 
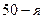единица.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки.
Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значения изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение).
Целесообразно отбор начинать с середины первого интервала, например при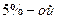 
выборке отобрать 
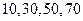и с таким же интервалом последующие единицы
Для определения средней ошибки механической выборки используется формула средней ошибки при собственно-случайном бесповторном отборе.
Типический отбор
Этот способ отбора используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп.
Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом.
Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.
При выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
,
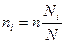где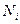 
- объем 
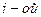группы;
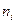- объем выборки из 
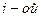группы.
Средняя ошибка такой выборки находится по формулам:
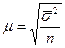- (повторный отбор); (2.1)
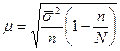- (бесповторный отбор), (2.2)
где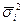 
- средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:
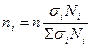, (2.3)
где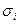 
- среднее квадратическое отклонение признака в 
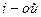группе.
Средняя ошибка такого отбора определяется следующим образом:
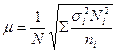- (повторный отбор), (2.4)
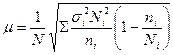- (бесповторный отбор). (2.5)
Рассмотрим оба варианта типической выборки на условном примере.
Предположим,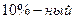 
бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности привел к следующим результатам (табл. 2.3).
Таблица 2.3
Результаты обследования рабочих предприятия
Рассчитаем выборочную среднюю:
.
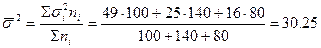Определим среднюю и предельную ошибки выборки (с вероятностью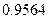 
):
;
.
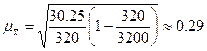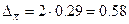Рассчитаем выборочную среднюю:
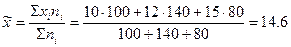
С вероятностью 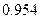можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:
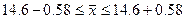
Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора, пропорционального дифференциации признака.
Определим необходимый объем выборки по каждому цеху:
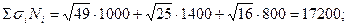
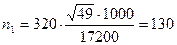человек;
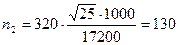человек;
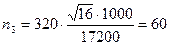человек;
С учетом полученных значений рассчитаем среднюю ошибку выборки:
.
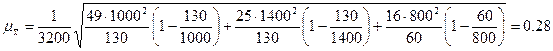В данном случае средняя, а, следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор
Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения.
Сущность серийной выборки заключается в собственно случайном либо механическом отборе серий, внутри который производится сплошное обследование единиц.
Средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
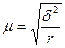(повторный отбор); (2.6)
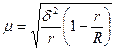(бесповторный отбор), (2.7)
где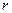 
- число отобранных серий;
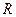- общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
,
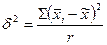где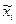 
- средняя 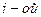серии;
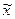- общая средняя по всей выборочной совокупности.
Комбинированный отбор
В практике статистических обследований помимо рассмотренных выше способов отбора применяется и их комбинация.
Можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из нескольких типических групп. Возможна также комбинация серийного и собственно-случайного отборов, при которой отдельное единицы отбираются внутри серии в собственно-случайном порядке.
Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом - более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка предполагает сохранение одной и той же единицы отбора на всех этапах его проведения, при этом отобранные на каждой стадии единицы подвергаются обследованию (на каждой последующей стадии отбора программа обследования расширяется).
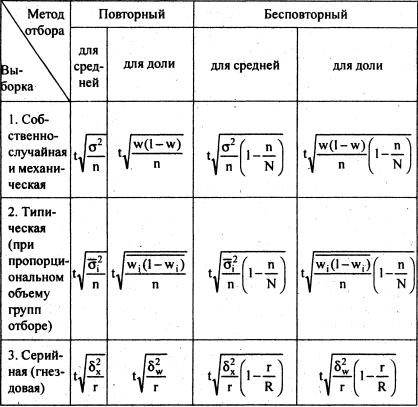
Исходя из вышеизложенного, приведем формулы предельной ошибки выборки для наиболее часто используемых на практике способов формирования выборочной совокупности (табл. 2.4).
Таблица 2.4
Предельная ошибка выборки для некоторых способов
формирования выборочной совокупности
ВЫБОЧНЫЕ НАБЛЮДЕНИЯ
Дата: 2019-02-02, просмотров: 433.
