1. После получения экспериментальных данных в виде статистического ряда его анализируют и исключают систематические ошибки.

2. Анализируют ряд в целях обнаружения грубых ошибок и промахов:

устанавливают подозрительные значения 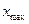 или ;

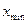определяют среднеквадратичное отклонение ;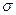

вычисляют по (2.6) критерии 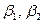 и сопоставляют с 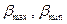, исключают при необходимости из статистического ряда  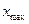или 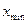 и получают новый ряд из новых членов.

3. Вычисляют среднеарифметическое 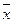, погрешности отдельных измерений  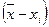и среднеквадратичное очищенного ряда .

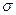4. Находят среднеквадратичное 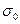 серии измерений, коэффициент вариации .

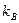5. При большой выборке задаются доверительной вероятностью 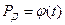 или уравнением значимости  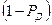и по табл.1.1 определяют .

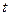6. При малой выборке ( 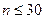) в зависимости от принятой доверительной вероятности  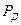и числа членов ряда  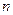принимают коэффициент Стьюдента 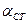; с помощью формулы (1.2) для большой выборки или (2.3) для малой выборки определяют доверительный интервал.

Таблица 2.2                                          Таблица 2.3

7. Устанавливают по (2.4) действительное значение исследуемой величины.

8. Оценивают относительную погрешность ( 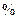) результатов серии измерений при заданной доверительной вероятности :

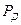.                                                                               (2.8)

Если погрешность серии измерений соизмерима с погрешностью прибора 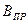, то границы доверительного интервала

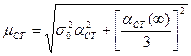.                                                                 (2.9)

Формулой (2.9) следует пользоваться при .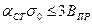

Если же 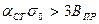, то доверительный интервал вычисляют с помощью (1.1) или (2.4).

Пример

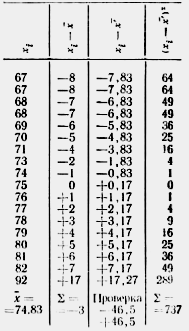
Пусть имеется 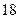 измерений (табл.2.3). Анализ средств и результатов измерений показал, что систематических ошибок в эксперименте не обнаружено. Необходимо выяснить, не содержат ли измерения грубых ошибок.

Если воспользоваться первым методом (критерий 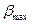), то надо вычислить среднеарифметическое  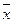и отклонение .

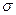При этом удобно пользоваться формулой

,

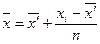где 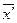 - среднее произвольное число.

Если принять 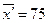 то .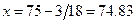

В формуле (1.1) значение 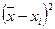 можно найти упрощенным методом:

.

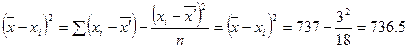Используя (1.1), получим

; .

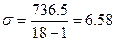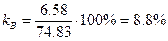Следовательно

.

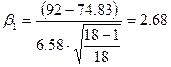Как видно из табл.2.1, при доверительной вероятност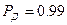и  и .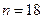

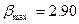Поскольку 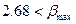 измерение  не является грубым промахом.

Если 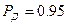,  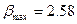то значение  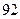следует исключить.

Если применить правило , то

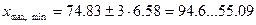
т.е. измерение 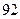 следует оставить.

В случае, когда измерение 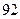 исключается,

;

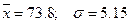Среднеквадратичное отклонение для всей серии измерений

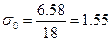при .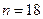

При очищенном ряде

.

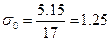Поскольку 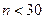, ряд следует отнести к малой выборке, и доверительный интервал вычисляется с применением коэффициента Стьюдента .

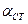По табл.1.2 принимается доверительная вероятность 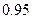 и тогда

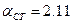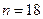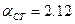при ;

при .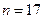

Доверительный интервал

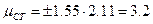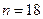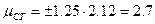при ;

при .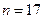

Действительное значение измеряемой величины:

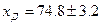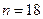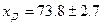при ;

при .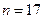

Относительная погрешность результатов серии измерений:

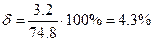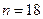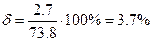при ;

при .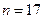

Таким образом, если принять 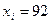 за грубый промах, то погрешность измерения уменьшается с  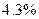до 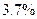 т.е. на .

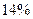Если необходимо вычислить минимальное количество измерений при заданной точности, проводят серию опытов, вычисляют 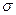, затем с помощью формулы (2.2) определяют .

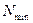В рассмотренном случае .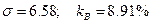

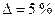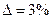Пусть задана точность  и  при доверительной вероятност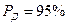и  и .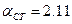

Тогда

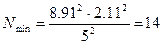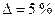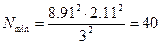при ;

при .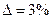

Таким образом, требование повышения точности измерения (но не выше точности прибора) приводит к значительному увеличению повторяемости опытов.

Выше были рассмотрены общие методы проверки экспериментальных измерений на точность и достоверность.

Ответственные эксперименты должны быть проверены и на воспроизводимость результатов, т.е. на их повторяемость в определенных пределах измерений с заданной| доверительной достоверностью.