Если расчет проводится по качественному альтернативному признаку и неизвестна его доля в генеральной совокупности (хотя бы приблизительно), рекомендуется принять ее равной 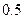, так как дисперсия доли достигает максимума:  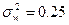при .

Пр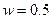еимущество такого приема заключается в том, что он позволяет определить численность выборочной совокупности, не располагая данными предыдущих обследований, и не проводить пробных обследований.

Если же качественный признак, по которому определяется необходимая численность выборочной совокупности, не является альтернативным, то использовать формулу 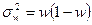 нельзя.

В ряде случаев приближенная оценка колеблемости может быть осуществлена с помощью превращения изучаемого признака в альтернативный.

Например, все категории работников предприятия можно условно разделить в зависимости от принадлежности работающих к рабочим и служащим. Однако при этом следует учитывать, что такое деление неизбежно приведет к потере некоторой части информации. Ведь существуют отдельные категории работников (МОП, охрана и др.), которые выделяются в самостоятельные группы. Поэтому применять описанный выше прием можно лишь при условии, что существует уверенность в незначительной доле неучтенных единиц во всей совокупности.

Приведем формулы необходимого объема выборки для наиболее часто используемых на практике способов формирования выборочной совокупности (табл. 1.1).

Рассмотрим несколько примеров расчета объема выборки при различных способах отбора.

Пример 1

В микрорайоне проживает 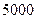 семей.

В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать 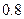 человека с вероятностью  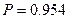и при среднем квадратическом отклонении  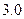человека (ошибка и среднее квадратическое отклонение определены на основе пробного обследования).

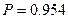
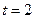
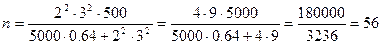При

 семей

Пример 2

Для определения средней длины детали следует провести выборочное обследование методом случайного повторного отбора. Какое количество деталей надо отобрать, чтобы ошибка выборки не превышала 3 мм с вероятностью 0,997 при среднем квадратическом отклонении 6 мм?*

При t = 3 и Р = 0,997 объем выборки рассчитывается следующим образом:

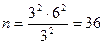 деталей.

Пример 3

В фермерских хозяйствах области 10 000 коров. Из них в районе А-5000, в районе Б-3000, в районе В-2000. С целью определения средней удойности предполагается провести типическую выборку коров с пропорциональным отбором внутри групп (механическим).

Какое количество коров следует отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 л, если на основе предыдущих обследований известно, что дисперсия типической выборки равна 1600?

Рассчитаем необходимую численность типической выборки:

.

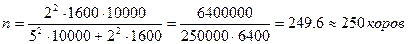Необходимо отобрать 250 коров, из них:

в районе А: ;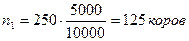

в районе Б: ;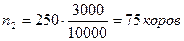

в районе В: .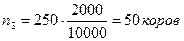

Ошибка и среднее квадратическое отклонение заданы исходя из технических нормативов.

Пример 4

На склад АО «Машиностроитель» поступило 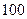 ящиков готовых изделий по  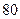шт. в каждом. Для установления среднего веса деталей следует провести серийную выборку деталей методом механического отбора так; чтобы с вероятностей  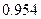ошибка выборки не превышала  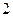г. На основе предыдущих обследований известно, что дисперсия серийной выборки равна 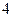. Определить необходимый объем выборки.

.

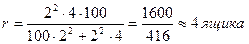Подробное рассмотрение вопросов определения дисперсии для нахождения объема выборки не исключает использования в этих целях других показателей вариации.