Во-первых, «отсечение» приводит к еще большему, если учитывать невозвращенные и забракованные формуляры, уменьшению объема выборки.

Во-вторых, из обработки и анализа исключаются вполне пригодные для исследования формуляры.

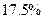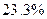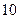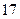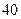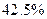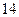В нашем примере «отсекаются»  собранных формуляров по группе рабочих и примерно  -по группе служащих. Сами по себе эти показатели весьма значительны. Однако и они могут возрасти, если для обработки окажутся пригодными не 10, а, скажем, анкет студентов. Тогда из обработки потребуется исключить  из  анкет рабочих ( ) и  из 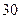 анкет служащих (около ).

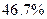В таких случаях целесообразнее пользоваться способом «взвешивания».

В отличие от первого способа корректировки «взвешивание» дает возможность сохранить в обрабатываемом массиве все или почти все полученные формуляры. Достигается это путем многократного использования при обработке части формуляров. При этом несколько раз используются, как правило, те формуляры, число которых настолько мало, что вызывает необходимость исключения из дальнейшей обработки большого числа для исследования формуляров, относящихся к другим группам. Многократное применение формуляров проводится на основе специально рассчитанных для этой цели «весов».

Метод «взвешивания» наиболее удобно применять при обработке материалов выборочных обследований в случаях высокого процента невозвращенных или забракованных формуляров. Это характерно прежде для почтовых опросов.

Собранные в результате выборочного наблюдения и при необходимости откорректированные данные распространяются на генеральную совокупность.

Существуют два основных метода распространения - прямой пересчет и способ коэффициентов.

Прямой пересчет

Способ прямого пересчета заключается в умножении среднего значения признака, найденного в результате выборочного наблюдения, на объем генеральной совокупности.

Например, на основании выборочного обследования 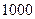 молодых семей требуется оценить потребность в местах в детских яслях.

Известно, что ясли могут посещать дети в возрасте до трех лет. По материалам выборочного обследования следует вычислить среднее число детей этого возраста. Предположим, что оно составляет 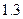 человека.

Умножив это число на численность генеральной совокупности, получим, что в детских яслях потребуется выделить 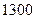 мест.

Производя такие расчеты, мы считаем, что были обследованы все единицы, попавшие в выборочную совокупность.

Однако в социальных исследованиях объемы фактической и запланированной выборки часто не совпадают, что всегда следует учитывать. Как правило, несоответствие фактической и запланированной выборки приводит, естественно, к неадекватному отражению в выборочных характеристиках, полученных по фактическим данным соответствующих характеристик генеральной совокупности.

Предположим, в нашем примере некоторое число семей по тем или иным причинам не было обследовано. Это привело к снижению объема фактической выборки по сравнению с запланированной.

Среднее число детей, вычисленное по этой «неполной» выборке, составило не 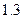, а 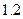. Тогда прямой пересчет выборочной характеристики на объем генеральной совокупности даст результа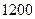т  мест.

Абсолютное отклонение от необходимого количества мест при условии охвата обследованием всей выборочной совокупности составит 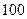 мест, а относительное - приблизительно .

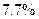Если же объем генеральной совокупности был бы в 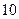 раз больше, т.е.  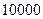семей, то абсолютное отклонение также увеличится в  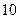раз и при сохранении тех же различий среднего числа детей составит  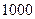мест, относительное отклонение при этом не изменится.

Таким образом, размер абсолютного отклонения находится в прямой зависимости от объема генеральной совокупности.

Данный пример показывает: недоучет обстоятельства, при котором на практике объемы фактической и запланированной выборок часто не совпадают, приводит к серьезным ошибкам при использовании распространенных на генеральную совокупность результатов таких исследований.

Руководствуясь данными, рассчитанными на условном примере, пришлось бы принимать ошибочное решение о строительстве дополнительного числа детских учреждений, мест в которых не хватило бы на 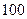 (или на  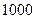- в зависимости от объема генеральной совокупности) детей. Но могла возникнуть и обратная ситуация, когда вычисленное по «неполной» выборочной совокупности среднее число детей оказалось бы больше «истинного». В этом случае появились бы «лишние» места.

Данный пример показывает, что результатами выборочного наблюдения необходимо пользоваться осторожно, особенно в случаях, когда их использование связано с большими материальными затратами.

Способ коэффициентов

Данный способ целесообразно использовать в случаях, когда выборочное наблюдение проводится с целью проверки и уточнения данных сплошного наблюдения, в частности численности учтенных единиц совокупности.

При этом следует использовать следующую формулу:

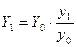,                                                                                         (2.3)

где 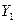 - численность совокупности с поправкой на недоучет;

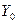 - численность совокупности без этой поправки;

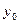 - численность совокупности в контрольные точках по первоначальным

данным;

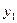 - численность совокупности в тех же точках по данным контрольных

мероприятий.

Отметим, что цели исследования многих явлений могут быть достигнуты только путем сплошного наблюдения. Поэтому способ проверки результатов сплошного наблюдения на основе коэффициентов успешно применяется в социальной и экономической статистике.