при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;

большие погрешности встречаются реже, чем малые (вероятность появления погрешности уменьшается с ростом ее величины);

при бесконечно большом числе измерении истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений;

появление того или иного результата измерения как случайного события описывается нормальным законом распределения.

На практике различают генеральную и выборочную совокупность измерений.

Под генеральной совокупностью подразумевают все множество возможных значений измерений 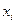 или возможных значений погрешностей .

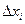Для выборочной совокупности число измерений 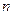 ограничено, и в каждом конкретном случае строго определяется. Считают, что, если 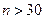, то среднее значение данной совокупности измерений  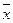достаточно приближается к его истинному значению.

Интервальная оценка с помощью доверительной вероятности

Для большой выборки и нормального закона распределения общей оценочной характеристикой измерения являются дисперсия 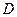 и коэффициент вариации :

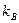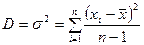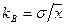; .                                                  (1.1)

Дисперсия характеризует однородность измерения. Чем выше 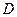, тем больше разброс измерений.

Коэффициент вариации характеризует изменчивость. Чем выше 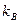, тем больше изменчивость измерений относительно средних значений.

Для оценки достоверности результатов измерений вводятся в рассмотрение понятия доверительного интервала и доверительной вероятности.

Доверительным называется интервал значений 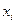, в который попадает истинное значение  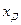измеряемой величины с заданной вероятностью.

Доверительной вероятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал, т.е. в зону 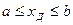. Эта величина определяется в долях единицы или в процентах

,

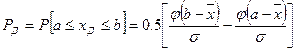где 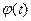 - интегральная функция Лапласа (табл.1.1)

Интегральная функция Лапласа определяется следующим выражением:

.

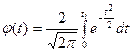Аргументом этой функции является гарантийный коэффициент:

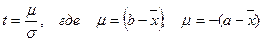.                                           (1.2)

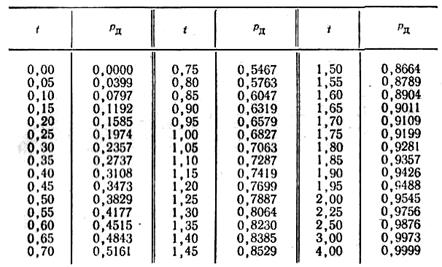
Таблица 1.1

Интегральная функция Лапласа

Если же на основе определенных данных установлена доверительная вероятность 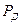 (часто ее принимают равной 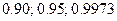), то устанавливается точность измерений (доверительный интервал 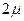) на основе соотношения

.

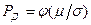Половина доверительного интервала равна

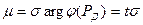,                                                                         (1.3)

где 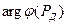 - аргумент функции Лапласа, если  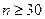(табл.1.1);

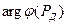 - функции Стьюдента, если  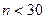(табл.1.2).