Метод ее расчета наиболее широко применяется в обследованиях относительно небольших совокупностей, когда их объем не превышает нескольких сотен или тысяч единиц.

Пример

При проведении учета коммерческих палаток в городе было зарегистрировано следующее их количество в районах: 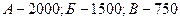. С целью проверки данных сплошного учета проведены контрольные обходы части обследованных районов. Их результаты содержатся в табл. 2.1.

Рассчитанный по каждой категории работников коэффициент недоучета является основой уточнения при распространении данных, полученных при выборочных контрольных мероприятиях, на всю совокупность.

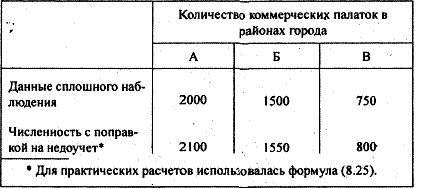
Таблица 2.1

Количество коммерческих палаток в районах города до и после

контрольных обходов

В нашем примере количество коммерческих палаток (по данным сплошного учета) следует умножить на рассчитанный для каждого района коэффициент недоучета. В итоге получим результаты, представленные в табл. 2.2.

Таблица 2.2

Уточненные данные учета коммерческих палаток

В 13 районах города

Применение метода коэффициентов связано, как правило, с использованием выборочного наблюдения с целью проверки данных сплошного наблюдения. Однако это приводит к сознательному ограничению области применения данного метода.

Метод коэффициентов можно использовать для проверки данных выборочного наблюдения, когда необходима очень высокая точность результатов и выборочная совокупность имеет большой объем - порядка нескольких тысяч или десятков тысяч единиц. В таких случаях списки единиц обследованной выборочной совокупности служат основой для отбора единиц в «контрольную» выборку, т.е. производителя выборка из выборки.

Контроль и, если это необходимо, уточнение данных основного обследования проводятся по методике, описанной выше на условном примере. Способ поправочных коэффициентов целесообразно использовать для распространения данных выборочного наблюдения в случаях, если его результаты значительно уступают в точности данным статистической отчетности или точность собранного статистического материала вызывает сомнение.

МАЛАЯ ВЫБОРКА

В процессе оценки степени представительности данных выборочного наблюдения важное значение приобретает вопрос об объеме выборочной совокупности .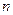

От него зависит не только величина пределов, которые с данной вероятностью не превзойдет ошибка выборки, но и способы определения этих пределов.

При большом числе единиц выборочной совокупности ( 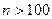) распределение случайных ошибок выборочной средней в соответствии с теоремой Ляпунова нормально или приближается к нормальному по мере увеличения числа наблюдений.

Вероятность выхода ошибки за определенные пределы оценивается на основе таблиц интеграла Лапласа. Расчет ошибки выборки базируется на величине генеральной дисперсии 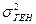, так как при больших  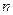коэффициент 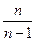, на который для получения генеральной умножается выборочная дисперсия, большой роли не играет.

В практике статистического исследования часто приходится сталкиваться с небольшими по объему так называемыми малыми выборками.