Ошибки регистрации могут иметь случайный (непреднамеренный) или систематический (тенденциозный) характер. Их можно избежать при правильной организации и проведении наблюдения.

Ошибки репрезентативности органически присущи выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную.

Избежать ошибок репрезентативности нельзя, однако, пользуясь методами теории вероятностей, основанными на использовании предельных теорем закона больших чисел, эти ошибки можно свести к минимальным значениям, границы которых устанавливаются с достаточно большой точностью;

Ошибка выборочного наблюдения - это разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения.

Для среднего значения ошибка будет определяться так:

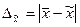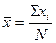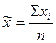, где , .                                          (1.1)

Величина 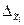 называется предельной ошибкой выборки.

Предельная ошибка выборки величина случайная. Исследованию закономерностей случайных ошибок выборки посвящены предельные теоремы закона больших чисел.

Наиболее полно эти закономерности раскрыты в теоремах Л.Л. Чебышева и А.М. Ляпунова.

Теорема П. Л. Чебышева: при достаточно большом числе независимых наблюдений можно с вероятностью, близкой к единице (т.е. почти с достоверностью), утверждать, что отклонение выборочной средней от генеральной будет сколько угодно малым.

В теореме доказано, что величина ошибки не должна превышать .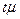

В свою очередь, величина 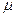, выражающая среднее квадратическое отклонение выборочной средней от генеральной средней, зависит от колеблемости признака в генеральной совокупности  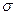и числа отобранных единиц .

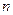Эта зависимость выражается формулой

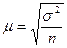,                                                                                            (1.2)

где 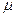 - средняя ошибка выборки (зависит и от способа производства выборки);

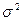 - генеральная дисперсия;

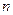 - объем выборочной совокупности.

Нетрудно убедиться, что при отборе большого числа единиц расхождения между средними будут меньше, т.е. существует обратная связь между, средней ошибкой выборки и числом отобранных единиц.

Можно доказать, что увеличение колеблемости признака влечет за собой увеличение среднего квадратического отклонения, а, следовательно, и ошибки.

Соотношение между дисперсиями генеральной и выборочной совокупности выражается формулой

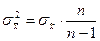.                                                                                        (1.3)

Так как величина 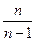 при достаточно больших  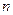близка к 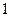, можно приближенно считать, что выборочная дисперсия равна генеральной дисперсии, т.е. .

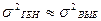Следовательно, средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью. На величину вероятности указывает множитель .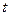

А. М. Ляпунов доказал, что распределение выборочных средних (а, следовательно, и их отклонений от генеральной средней) при достаточно большом числе независимых наблюдений приближенно нормально при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.

Математически теорему Ляпунова можно записать так:

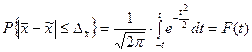,                                              (1.4)

где 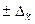 - предельная ошибка выборки.

Значения этого интеграла для различных значений коэффициента доверия  вычислены и приводятся в специальных математических таблицах.

Например:

t = 1 F (t) = 0.683;            t = 1.5 F (t) = 0.866;

t = 2 F (t) = 0.954;            t = 2.5 F (t) = 0.988;

t = 3 F (t) = 0.997;            t = 3.5 F (t) = 0.999.

Это может быть прочитано так: с вероятностью 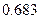 можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки.

Другими словами, в 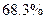 случаев ошибка репрезентативности не выйдет за пределы  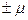и т.д.

Зная выборочную среднюю величину признака 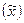 и предельную ошибку выборки , можно определить границы (пределы), в которых заключена генеральная средняя:

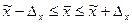или .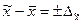

Теорема Бернулли рассматривает ошибку выборки для альтернативного признака, у которого возможны только два исхода: наличие признака ( 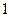) и отсутствие его (0).

Теорема Бернулли утверждает, что при достаточно большом объеме выборки вероятность расхождения между долей признака в выборочной совокупности ( 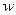) и долей признака в генеральной совокупности ( 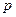) будет стремиться к единице:

,

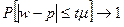Т.е. с вероятностью, сколько угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки частость признака (выборочная доля) сколько угодно мало будет отличаться от доли признака (в генеральной совокупности).

Ввиду того, что вероятность расхождения между частостью и долей следует закону нормального распределения, эту вероятность можно найти по функции  в зависимости от задаваемой величины .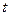

Средняя ошибка выборки для альтернативного признака определяется по формуле

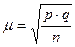, где 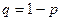.                                                          (1.5)

Поскольку доля признака в выборочной совокупности неизвестна, ее необходимо заменить через долю того же признака в генеральной совокупности, т.е. принять 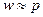, а дисперсию альтернативного признака принять за .

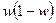Тогда средняя, ошибка выборки выразится формулой

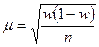.                                                                                    (1.6)

Предельная величина разности между частостью и долей называется предельной ошибкой выборки.

О величине предельной ошибки можно судить с некоторой вероятностью, которая зависит от множителя 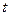, поскольку .

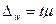Зная выборочную долю признака 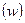 и предельную ошибку выборки 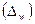, можно определить границы, в которых заключена генеральная доля :

.

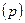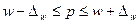Результаты выборочного статистического исследования во многом зависят от уровня подготовки процесса наблюдения.

Под уровнем подготовки в данном случае подразумевается соблюдение определенных правил и принципов проектирования выборочного обследования. Важнейшим элементом проектирования является составление организационного плана выборочного наблюдения.

В организационный план включаются следующие вопросы:

1. Постановка цели и задачи наблюдения.

2. Определение границ объекта исследования.

3. Отработка программы наблюдения (составление анкеты, опросного листа, формы отчета и т.д.) и разработка ее материалов.

4. Определение процедуры отбора, способа отбора и объема выборки.

5. Подготовка кадров для проведения наблюдения, размножение формуляров, инструктивных документов и др.

6. Расчет выборочных характеристик и определение ошибок выборки.

7. Распространение выборочных данных на всю совокупность.

2.2 ОСНОВНЫЕ СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ

Достоверность рассчитанных по выборочным данным характеристик в значительной степени определяется репрезентативностью выборочной совокупности, которая, в свою очередь, зависит от способа отбора единиц из генеральной совокупности.

По виду различают индивидуальный, групповой и комбинированный отбор.

При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе - группы единиц, а комбинированный отбор предполагает сочетание группового и индивидуального отбора.

Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.

Бесповторным называется такой отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.

При повторном отборе попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процедуре отбора.

При этом методе объем генеральной совокупности остается неизменным, что обусловливает постоянную вероятность попадания в выборку всех единиц совокупности.

В практике выборочных обследований наибольшее распространение получи ли следующие выборки:

собственно-случайная;

механическая;

типическая;

серийная;

комбинированная.

Собственно-случайная выборка

При такой выборке отбор единиц из генеральной совокупности производится наугад или наудачу, без каких-либо элементов системности. При этом все без исключения единицы генеральной совокупности должны иметь абсолютно равные шансы попадания в выборку.

Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.

Собственно-случайный отбор может быть как повторным, так и бесповторным.

Предположим, в результате выборочного обследования жилищных условий жителей города, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл. 2.1).

Таблица 2.1