Для проведения опытов с заданной точностью и достоверностью необходимо знать то количество измерений, при котором экспериментатор уверен в положительном исходе.
В связи с этим одной из первоочередных задач при статистических методах оценки является установление минимального, но достаточного числа измерении для данных условий.
Задача сводится к установлению минимального объема выборки (числа измерении)  при заданных значениях доверительного интервала
при заданных значениях доверительного интервала 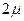 и доверительной вероятности
и доверительной вероятности  .
.
При выполнении измерений необходимо знать их точность:
 , (2.1)
, (2.1)
где  - среднеарифметическое значение среднеквадратического отклонения
- среднеарифметическое значение среднеквадратического отклонения  .
.
Значение  часто называют средней ошибкой.
часто называют средней ошибкой.
Доверительный интервал ошибки измерения  определяется выражением
определяется выражением
 .
.
С помощью 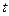 легко определить доверительную вероятность ошибки измерений по табл.1.1.
легко определить доверительную вероятность ошибки измерений по табл.1.1.
В исследованиях часто по заданной точности  и доверительной вероятности измерения определяют минимальное количество измерений, гарантирующих требуемые значения
и доверительной вероятности измерения определяют минимальное количество измерений, гарантирующих требуемые значения  и
и 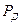 .
.
При  получаем
получаем
 , (2.2)
, (2.2)
Для определения  может быть принята такая последовательность вычислений.
может быть принята такая последовательность вычислений.
1. Проводится предварительный эксперимент с количеством измерений  , которое составляет в зависимости от трудоемкости опыта от
, которое составляет в зависимости от трудоемкости опыта от  до
до  .
.
2. Вычисляется среднеквадратическое отклонение  по формуле (1.1).
по формуле (1.1).
3. В соответствии с поставленными задачами эксперимента устанавливается требуемая точность измерений  , которая не должна превышать точности прибора.
, которая не должна превышать точности прибора.
4. Устанавливается нормированное отклонение 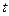 , значение которого обычно задается (зависит также от точности метода).
, значение которого обычно задается (зависит также от точности метода).
5. По формуле (2.2) определяют  и в дальнейшем в процессе эксперимента число измерений не должно быть меньше
и в дальнейшем в процессе эксперимента число измерений не должно быть меньше  .
.
Пример
При приемке сооружений комиссия в качестве одного из параметров замеряет их ширину. Согласно инструкции требуется выполнять 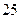 измерений. Допускаемое отклонение параметра
измерений. Допускаемое отклонение параметра 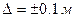 . Если предварительно вычисленное значение
. Если предварительно вычисленное значение 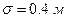 , то можно определить, с какой достоверностью комиссия оценивает данный параметр.
, то можно определить, с какой достоверностью комиссия оценивает данный параметр.
Из формулы (2.2) можно записать
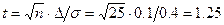 .
.
В соответствии с табл.10.1 доверительная вероятность для 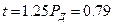 .
.
Это низкая вероятность.
Погрешность, превышающая доверительный интервал 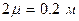 , согласно выражению (1.4) будет встречаться один раз из
, согласно выражению (1.4) будет встречаться один раз из 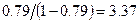 , т.е. из четырех измерений. Это недопустимо.
, т.е. из четырех измерений. Это недопустимо.
В связи с этим необходимо вычислить минимальное количество измерений с доверительной вероятностью 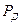 , равной
, равной 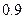 и
и 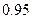 .
.
По формуле (2.2) имеем 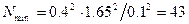 измерения при
измерения при 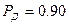 и
и 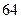 измерения при
измерения при 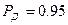 , что значительно превышает установленные
, что значительно превышает установленные 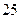 измерений.
измерений.
Для нахождения границы доверительного интервала при малых значениях ( 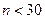 ) применяют метод, предложенный в 1908 г. английским математиком Госсетом В.С. (псевдоним Стьюдент).
) применяют метод, предложенный в 1908 г. английским математиком Госсетом В.С. (псевдоним Стьюдент).
Кривые распределения Стьюдента в случае 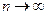 (практически при
(практически при 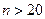 ) переходят в кривые нормального распределения (рис.10.1).
) переходят в кривые нормального распределения (рис.10.1).
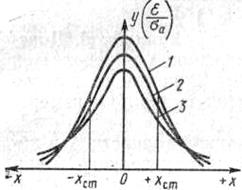
Рис.2.1. Кривые распределения Стьюдента для различных значений:
1 - при 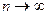 ; 2 - при
; 2 - при 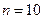 ; 3 - при
; 3 - при 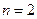
Дата: 2019-02-02, просмотров: 1056.