Методы математической статистики.
Выборочные наблюдения.
1 Основы теории случайных ошибок и методов оценки случайных погрешностей в измерениях
Анализ случайных погрешностей основывается на теории случайных ошибок, дающей возможность с определенной гарантией вычислить действительное значение измеренной величины и оценить возможные ошибки.
Основу теории случайных ошибок составляют следующие предположения:
при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;
большие погрешности встречаются реже, чем малые (вероятность появления погрешности уменьшается с ростом ее величины);
при бесконечно большом числе измерении истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений;
появление того или иного результата измерения как случайного события описывается нормальным законом распределения.
На практике различают генеральную и выборочную совокупность измерений.
Под генеральной совокупностью подразумевают все множество возможных значений измерений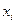 
или возможных значений погрешностей 
.
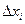Для выборочной совокупности число измерений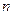 
ограничено, и в каждом конкретном случае строго определяется. Считают, что, если 
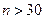, то среднее значение данной совокупности измерений 
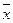достаточно приближается к его истинному значению.
Интервальная оценка с помощью доверительной вероятности
Для большой выборки и нормального закона распределения общей оценочной характеристикой измерения являются дисперсия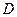 
и коэффициент вариации 
:
; 
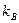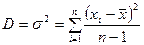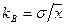. (1.1)
Дисперсия характеризует однородность измерения. Чем выше 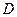, тем больше разброс измерений.
Коэффициент вариации характеризует изменчивость. Чем выше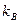 
, тем больше изменчивость измерений относительно средних значений.
Для оценки достоверности результатов измерений вводятся в рассмотрение понятия доверительного интервала и доверительной вероятности.
Доверительным называется интервал значений 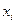, в который попадает истинное значение 
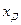измеряемой величины с заданной вероятностью.
Доверительной вероятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал, т.е. в зону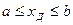 
. Эта величина определяется в долях единицы или в процентах
,
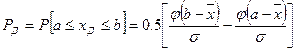где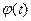 
- интегральная функция Лапласа (табл.1.1)
Интегральная функция Лапласа определяется следующим выражением:
.
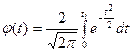Аргументом этой функции является гарантийный коэффициент:
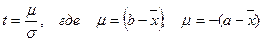. (1.2)
Таблица 1.1
Пример
Выполнено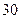 
измерений прочности дорожного покрытия участка автомобильной дороги при среднем модуле упругости 
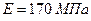и вычисленном значении среднеквадратического отклонения 
.
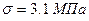Необходимо определить требуемую точность измерений для разных уровней доверительной вероятности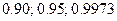 
, приняв значения 
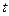по табл.1.1.
В этом случае соответственно |
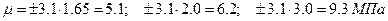
Следовательно, для данного средства и метода измерений доверительный интервал возрастает примерно в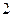 
раза, если увеличить 
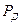только на 
.
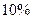Таблица 1.2
Коэффициент Стьюдента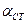 
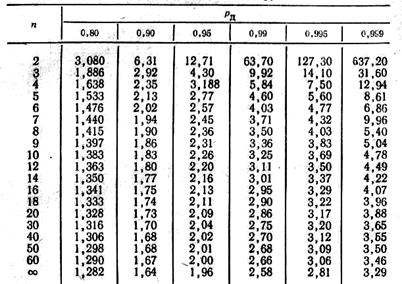
Пример
Определить достоверность измерений для установленного доверительного интервала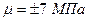 
.
По формуле (1.2) имеем: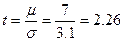 
.
По табл.1.1 для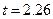 
определяем 
.
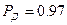Это означает, что в заданный доверительный интервал из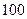 
измерений не попадают только 
.
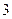Значение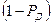 
называют уровнем значимости. Из него следует, что при нормальном законе распределения погрешность, превышающая доверительный интервал, будет встречаться один раз из 
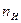измерений, где
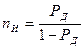. (1.4)
Это означает, что приходится браковать одно из 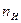измерений.
По данным приведенных выше примеров можно вычислить количество измерений, из которых одно измерение превышает доверительный интервал.
Если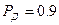 
, то по формуле (1.4) определяется 
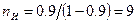измерений.
Если 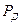равна 
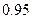и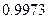 
, соответственно 
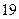и 
и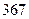змерений.
Пример
При приемке сооружений комиссия в качестве одного из параметров замеряет их ширину. Согласно инструкции требуется выполнять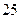 
измерений. Допускаемое отклонение параметра 
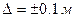. Если предварительно вычисленное значение 
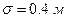, то можно определить, с какой достоверностью комиссия оценивает данный параметр.
Из формулы (2.2) можно записать
.
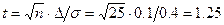В соответствии с табл.10.1 доверительная вероятность для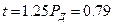 
.
Это низкая вероятность.
Погрешность, превышающая доверительный интервал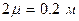 
, согласно выражению (1.4) будет встречаться один раз из 
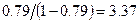, т.е. из четырех измерений. Это недопустимо.
В связи с этим необходимо вычислить минимальное количество измерений с доверительной вероятностью 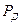, равно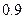й 
и .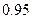
По формуле (2.2) имеем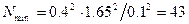 
измерения при 
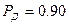и 
и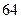змерения при 
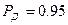, что значительно превышает установленные 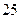измерений.
Для нахождения границы доверительного интервала при малых значениях (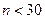 
) применяют метод, предложенный в 1908 г. английским математиком Госсетом В.С. (псевдоним Стьюдент).
Кривые распределения Стьюдента в случае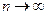 
(практически при 
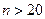) переходят в кривые нормального распределения (рис.10.1).
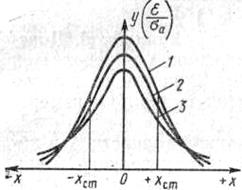
Рис.2.1. Кривые распределения Стьюдента для различных значений:
1 - при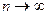 
; 2 - при 
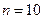; 3 - при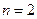 
Пример
Пусть имеется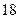 
измерений (табл.2.3). Анализ средств и результатов измерений показал, что систематических ошибок в эксперименте не обнаружено. Необходимо выяснить, не содержат ли измерения грубых ошибок.
Если воспользоваться первым методом (критерий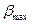 
), то надо вычислить среднеарифметическое 
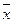и отклонение 
.
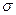При этом удобно пользоваться формулой
,
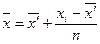где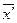 
- среднее произвольное число.
Если принять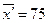 
то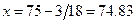 
.
В формуле (1.1) значение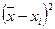 
можно найти упрощенным методом:
.
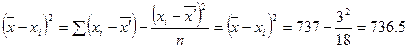Используя (1.1), получим
; 
.
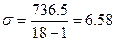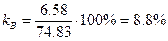Следовательно
.
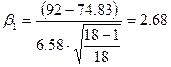Как видно из табл.2.1, при доверительной вероятност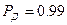и 
и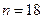 
.
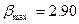Поскольку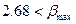 
измерение 
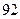не является грубым промахом.
Если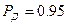 
, 
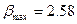то значение 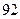следует исключить.
Если применить правил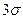о 
, то
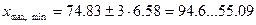
т.е. измерение 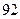следует оставить.
В случае, когда измерение 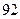исключается,
;
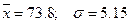Среднеквадратичное отклонение для всей серии измерений
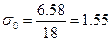при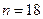 
.
При очищенном ряде
.
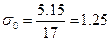Поскольку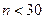 
, ряд следует отнести к малой выборке, и доверительный интервал вычисляется с применением коэффициента Стьюдента 
.
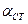По табл.1.2 принимается доверительная вероятность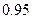 
и тогда
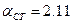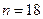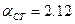при ;
при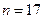 
.
Доверительный интервал
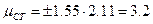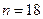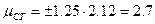при ;
при .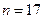
Действительное значение измеряемой величины:
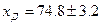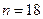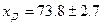при ;
при .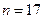
Относительная погрешность результатов серии измерений:
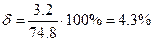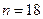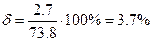при ;
при .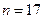
Таким образом, если принять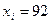 
за грубый промах, то погрешность измерения уменьшается с 
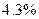до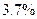 
т.е. на 
.
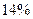Если необходимо вычислить минимальное количество измерений при заданной точности, проводят серию опытов, вычисляют 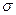, затем с помощью формулы (2.2) определяют 
.
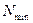В рассмотренном случае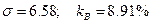 
.
Пусть задана точность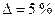 
и 
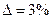при доверительной вероятност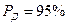и 
и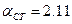 
.
Тогда
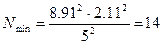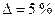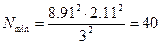при ;
при .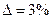
Таким образом, требование повышения точности измерения (но не выше точности прибора) приводит к значительному увеличению повторяемости опытов.
Выше были рассмотрены общие методы проверки экспериментальных измерений на точность и достоверность.
Ответственные эксперименты должны быть проверены и на воспроизводимость результатов, т.е. на их повторяемость в определенных пределах измерений с заданной| доверительной достоверностью.
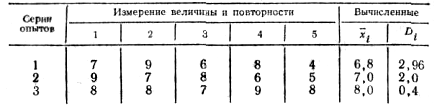
Таблица 2.5
Результаты измерений прочности грунта
Пример
Пусть проведено три серии опытов по измерению прочности грунта (табл.2.5).
В каждой серии выполнялось по пять измерений (повторностей).
Тогда по формуле (2.10)
.
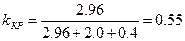Вычислим число степеней свободы
.
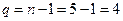Для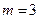 
и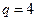 
согласно табл.2.4 значение критерия Кохрена 
.
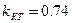Так как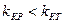 
, то измерения в эксперименте следует считать воспроизводимыми. Если бы оказалось наоборот, т.е. 
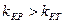, то необходимо было бы увеличить число серий 
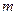или число измерений 
.
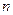Понятие статистики
Статистика, вернее ее методы исследования, широко применяется в различных областях человеческих знаний. Однако, как любая наука, она требует определения предмета ее исследования. В связи с этим различают статистику, занимающуюся изучением социально-экономических явлений, которая относится к циклу общественных наук, и статистику, занимающуюся закономерностями явлений природы, которая относится к наукам естественным.
Авторы большинства современных отечественных вузовских учебников по теории статистики (общей теории статистики) под статистикой понимают предметную общественную науку, т.е. науку, имеющую свои особые предмет и метод познания.
Статистика - общественная наука, которая изучает количественную сторону качественно определенных массовых социально-экономических явлений и процессов, их структуру и распределение, размещение в пространстве, движение во времени, выявляя действующие количественные зависимости, тенденции и закономерности, причем в конкретных условиях места и времени.
Предмет статистики
Статистика как наука исследует не отдельные факты, а массовые социально-экономические явления и процессы, выступающие как множество отдельных факторов, обладающих как индивидуальными, так и общими признаками.
Объект статистического исследования в статистике называют статистической совокупностью.
Статистическая совокупность - это множество единиц, обладающих массовостью, однородностью, определенной целостностью, взаимозависимостью состояния отдельных единиц и наличием вариации.
Например, в качестве особых объектов статистического исследования, т.е. статистических совокупностей, может выступать множество коммерческих банков, зарегистрированных на территории Российской Федерации, множество акционерных обществ, множество граждан какой-либо страны и т.д. Важно помнить, что статистическая совокупность состоит из реально существующих материальных объектов.
Каждый отдельно взятый элемент данного множества называется единицей статистической совокупности.
Единицы статистической совокупности характеризуются общими свойствами, именуемыми в статистике признаками, т.е. под качественной однородностью совокупности понимается сходство единиц (объектов, явлений, процессов) по каким-либо существенным признакам, но различающихся по каким-либо другим признакам.
Единицы совокупности наряду с общими для всех единиц признаками, обусловливающими качественную определенность совокупности, также обладают индивидуальными особенностями и различиями, отличающими их друг от друга, т.е. существует вариация признаков. Она обусловлена различным сочетанием условий, которые определяют развитие элементов множества.
Например, уровень производительности труда работников банка определяется его возрастом, квалификацией, отношением к труду и т.д.
Именно наличие вариации предопределяет необходимость статистики. Вариация признака может отражаться статистическим распределением единиц совокупности.
Статистика как наука изучает, прежде всего, количественную сторону общественных явлений и процессов в конкретных условиях места и времени, т.е. предметом статистики выступают размеры и количественные соотношения социально-экономических явлений, закономерности их связи и развития.
Количественную характеристику статистика выражает через определенного рода числа, которые называются статистическими показателями.
Статистический показатель отражает результат измерения у единиц совокупности и совокупности в целом.
Метод статистики
Статистика как наука выработала приемы и способы изучения массовых общественных явлений, зависящие от особенностей ее предмета и задач, которые ставятся при его изучении. Приемы и способы, с помощью которых статистика изучает свой предмет, образуют статистическую методологию.
Под статистической методологией понимается система приемов, способов и методов, направленных на изучение количественных закономерностей, проявляющихся в структуре, динамике и взаимосвязях социально-экономических явлений.
Задача статистического исследования состоит в получении обобщающих характеристик и выявлении закономерностей в общественной жизни в конкретных условиях места и времени, которые проявляются лишь в большой массе явлений через преодоление свойственной ее единичным элементам случайности.
Статистическое исследование состоит из трех стадий:
статистическое наблюдение;
сводка и группировка результатов наблюдения;
анализ полученных обобщающих показателей.
Все три стадии связаны между собой, и на каждой из них используются специальные методы, объясняемые содержанием выполняемой работы.
И выборочной совокупностей
Т.е. с вероятностью, сколько угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки частость признака (выборочная доля) сколько угодно мало будет отличаться от доли признака (в генеральной совокупности).
Ввиду того, что вероятность расхождения между частостью и долей следует закону нормального распределения, эту вероятность можно найти по функции 
в зависимости от задаваемой величины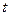 
.
Средняя ошибка выборки для альтернативного признака определяется по формуле
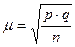, где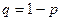 
. (1.5)
Поскольку доля признака в выборочной совокупности неизвестна, ее необходимо заменить через долю того же признака в генеральной совокупности, т.е. принять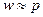 
, а дисперсию альтернативного признака принять за 
.
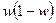Тогда средняя, ошибка выборки выразится формулой
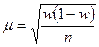. (1.6)
Предельная величина разности между частостью и долей называется предельной ошибкой выборки.
О величине предельной ошибки можно судить с некоторой вероятностью, которая зависит от множителя 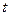, поскольку 
.
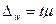Зная выборочную долю признака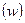 
и предельную ошибку выборки 
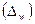, можно определить границы, в которых заключена генеральная доля 
:
.
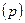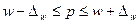Результаты выборочного статистического исследования во многом зависят от уровня подготовки процесса наблюдения.
Под уровнем подготовки в данном случае подразумевается соблюдение определенных правил и принципов проектирования выборочного обследования. Важнейшим элементом проектирования является составление организационного плана выборочного наблюдения.
В организационный план включаются следующие вопросы:
1. Постановка цели и задачи наблюдения.
2. Определение границ объекта исследования.
3. Отработка программы наблюдения (составление анкеты, опросного листа, формы отчета и т.д.) и разработка ее материалов.
4. Определение процедуры отбора, способа отбора и объема выборки.
5. Подготовка кадров для проведения наблюдения, размножение формуляров, инструктивных документов и др.
6. Расчет выборочных характеристик и определение ошибок выборки.
7. Распространение выборочных данных на всю совокупность.
2.2 ОСНОВНЫЕ СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ
Достоверность рассчитанных по выборочным данным характеристик в значительной степени определяется репрезентативностью выборочной совокупности, которая, в свою очередь, зависит от способа отбора единиц из генеральной совокупности.
По виду различают индивидуальный, групповой и комбинированный отбор.
При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе - группы единиц, а комбинированный отбор предполагает сочетание группового и индивидуального отбора.
Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.
Бесповторным называется такой отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.
При повторном отборе попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процедуре отбора.
При этом методе объем генеральной совокупности остается неизменным, что обусловливает постоянную вероятность попадания в выборку всех единиц совокупности.
В практике выборочных обследований наибольшее распространение получи ли следующие выборки:
собственно-случайная;
механическая;
типическая;
серийная;
комбинированная.
Собственно-случайная выборка
При такой выборке отбор единиц из генеральной совокупности производится наугад или наудачу, без каких-либо элементов системности. При этом все без исключения единицы генеральной совокупности должны иметь абсолютно равные шансы попадания в выборку.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Собственно-случайный отбор может быть как повторным, так и бесповторным.
Предположим, в результате выборочного обследования жилищных условий жителей города, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл. 2.1).
Таблица 2.1
Жителей города
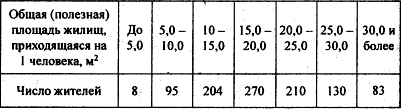
Для определения средней ошибки выборки необходимо рассчитать выборочную среднюю величину и дисперсию изучаемого признака (табл. 2.2).
Таблица 2.2
Таблица 2.3
Результаты обследования рабочих предприятия
Рассчитаем выборочную среднюю:
.
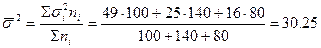Определим среднюю и предельную ошибки выборки (с вероятностью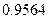 
):
;
.
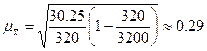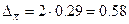Рассчитаем выборочную среднюю:
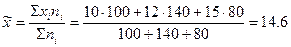
С вероятностью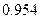 
можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:
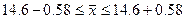
Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора, пропорционального дифференциации признака.
Определим необходимый объем выборки по каждому цеху:
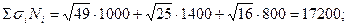
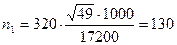человек;
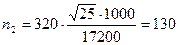человек;
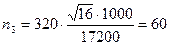человек;
С учетом полученных значений рассчитаем среднюю ошибку выборки:
.
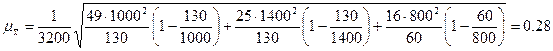В данном случае средняя, а, следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор
Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения.
Сущность серийной выборки заключается в собственно случайном либо механическом отборе серий, внутри который производится сплошное обследование единиц.
Средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
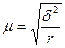(повторный отбор); (2.6)
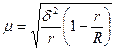(бесповторный отбор), (2.7)
где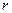 
- число отобранных серий;
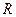- общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
,
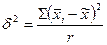где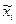 
- средняя 
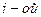серии;
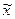- общая средняя по всей выборочной совокупности.
Комбинированный отбор
В практике статистических обследований помимо рассмотренных выше способов отбора применяется и их комбинация.
Можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из нескольких типических групп. Возможна также комбинация серийного и собственно-случайного отборов, при которой отдельное единицы отбираются внутри серии в собственно-случайном порядке.
Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом - более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка предполагает сохранение одной и той же единицы отбора на всех этапах его проведения, при этом отобранные на каждой стадии единицы подвергаются обследованию (на каждой последующей стадии отбора программа обследования расширяется).
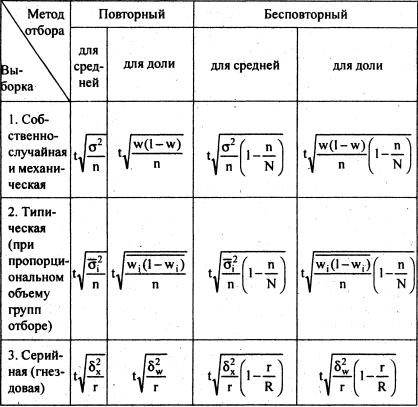
Исходя из вышеизложенного, приведем формулы предельной ошибки выборки для наиболее часто используемых на практике способов формирования выборочной совокупности (табл. 2.4).
Таблица 2.4
Предельная ошибка выборки для некоторых способов
формирования выборочной совокупности
ВЫБОЧНЫЕ НАБЛЮДЕНИЯ
Способ выражения качественных признаков не позволяет рассчитать по ним средние значения, поэтому оценка колеблемости производится, как правило, исходя из долей единиц, обладающих значениями этих признаков, т.е. выборочных долей.
Пример 1
В микрорайоне проживает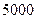 
семей.
В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать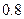 
человека с вероятностью 
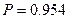и при среднем квадратическом отклонении 
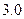человека (ошибка и среднее квадратическое отклонение определены на основе пробного обследования).
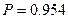
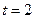
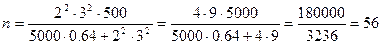При 
семей
Пример 2
Для определения средней длины детали следует провести выборочное обследование методом случайного повторного отбора. Какое количество деталей надо отобрать, чтобы ошибка выборки не превышала 3 мм с вероятностью 0,997 при среднем квадратическом отклонении 6 мм?*
При t = 3 и Р = 0,997 объем выборки рассчитывается следующим образом:
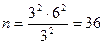деталей.
Пример 3
В фермерских хозяйствах области 10 000 коров. Из них в районе А-5000, в районе Б-3000, в районе В-2000. С целью определения средней удойности предполагается провести типическую выборку коров с пропорциональным отбором внутри групп (механическим).
Какое количество коров следует отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 л, если на основе предыдущих обследований известно, что дисперсия типической выборки равна 1600?
Рассчитаем необходимую численность типической выборки:
.
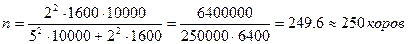Необходимо отобрать 250 коров, из них:
в районе А: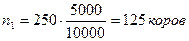 
;
в районе Б: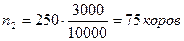 
;
в районе В: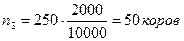 
.
Ошибка и среднее квадратическое отклонение заданы исходя из технических нормативов.
Пример 4
На склад АО «Машиностроитель» поступило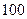 
ящиков готовых изделий по 
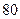шт. в каждом. Для установления среднего веса деталей следует провести серийную выборку деталей методом механического отбора так; чтобы с вероятностей 
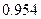ошибка выборки не превышала 
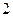г. На основе предыдущих обследований известно, что дисперсия серийной выборки равна 
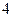. Определить необходимый объем выборки.
.
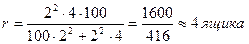Подробное рассмотрение вопросов определения дисперсии для нахождения объема выборки не исключает использования в этих целях других показателей вариации.
Прямой пересчет
Способ прямого пересчета заключается в умножении среднего значения признака, найденного в результате выборочного наблюдения, на объем генеральной совокупности.
Например, на основании выборочного обследования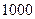 
молодых семей требуется оценить потребность в местах в детских яслях.
Известно, что ясли могут посещать дети в возрасте до трех лет. По материалам выборочного обследования следует вычислить среднее число детей этого возраста. Предположим, что оно составляет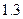 
человека.
Умножив это число на численность генеральной совокупности, получим, что в детских яслях потребуется выделить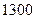 
мест.
Производя такие расчеты, мы считаем, что были обследованы все единицы, попавшие в выборочную совокупность.
Однако в социальных исследованиях объемы фактической и запланированной выборки часто не совпадают, что всегда следует учитывать. Как правило, несоответствие фактической и запланированной выборки приводит, естественно, к неадекватному отражению в выборочных характеристиках, полученных по фактическим данным соответствующих характеристик генеральной совокупности.
Предположим, в нашем примере некоторое число семей по тем или иным причинам не было обследовано. Это привело к снижению объема фактической выборки по сравнению с запланированной.
Среднее число детей, вычисленное по этой «неполной» выборке, составило не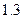 
, а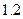 
. Тогда прямой пересчет выборочной характеристики на объем генеральной совокупности даст результат 
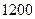мест.
Абсолютное отклонение от необходимого количества мест при условии охвата обследованием всей выборочной совокупности составит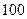 
мест, а относительное - приблизительно 
.
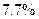Если же объем генеральной совокупности был бы в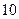 
раз больше, т.е. 
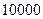семей, то абсолютное отклонение также увеличится в 
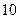раз и при сохранении тех же различий среднего числа детей составит 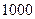мест, относительное отклонение при этом не изменится.
Таким образом, размер абсолютного отклонения находится в прямой зависимости от объема генеральной совокупности.
Данный пример показывает: недоучет обстоятельства, при котором на практике объемы фактической и запланированной выборок часто не совпадают, приводит к серьезным ошибкам при использовании распространенных на генеральную совокупность результатов таких исследований.
Руководствуясь данными, рассчитанными на условном примере, пришлось бы принимать ошибочное решение о строительстве дополнительного числа детских учреждений, мест в которых не хватило бы на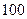 
(или на 
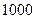- в зависимости от объема генеральной совокупности) детей. Но могла возникнуть и обратная ситуация, когда вычисленное по «неполной» выборочной совокупности среднее число детей оказалось бы больше «истинного». В этом случае появились бы «лишние» места.
Данный пример показывает, что результатами выборочного наблюдения необходимо пользоваться осторожно, особенно в случаях, когда их использование связано с большими материальными затратами.
Способ коэффициентов
Данный способ целесообразно использовать в случаях, когда выборочное наблюдение проводится с целью проверки и уточнения данных сплошного наблюдения, в частности численности учтенных единиц совокупности.
При этом следует использовать следующую формулу:
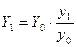, (2.3)
где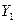 
- численность совокупности с поправкой на недоучет;
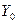- численность совокупности без этой поправки;
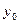- численность совокупности в контрольные точках по первоначальным
данным;
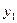- численность совокупности в тех же точках по данным контрольных
мероприятий.
Отметим, что цели исследования многих явлений могут быть достигнуты только путем сплошного наблюдения. Поэтому способ проверки результатов сплошного наблюдения на основе коэффициентов успешно применяется в социальной и экономической статистике.
Пример
При проведении учета коммерческих палаток в городе было зарегистрировано следующее их количество в районах: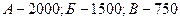 
. С целью проверки данных сплошного учета проведены контрольные обходы части обследованных районов. Их результаты содержатся в табл. 2.1.
Рассчитанный по каждой категории работников коэффициент недоучета является основой уточнения при распространении данных, полученных при выборочных контрольных мероприятиях, на всю совокупность.
Таблица 2.1
Количество коммерческих палаток в районах города до и после
контрольных обходов
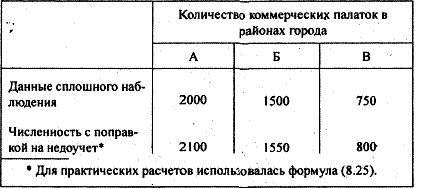
В нашем примере количество коммерческих палаток (по данным сплошного учета) следует умножить на рассчитанный для каждого района коэффициент недоучета. В итоге получим результаты, представленные в табл. 2.2.
Таблица 2.2
В 13 районах города
Применение метода коэффициентов связано, как правило, с использованием выборочного наблюдения с целью проверки данных сплошного наблюдения. Однако это приводит к сознательному ограничению области применения данного метода.
Метод коэффициентов можно использовать для проверки данных выборочного наблюдения, когда необходима очень высокая точность результатов и выборочная совокупность имеет большой объем - порядка нескольких тысяч или десятков тысяч единиц. В таких случаях списки единиц обследованной выборочной совокупности служат основой для отбора единиц в «контрольную» выборку, т.е. производителя выборка из выборки.
Контроль и, если это необходимо, уточнение данных основного обследования проводятся по методике, описанной выше на условном примере. Способ поправочных коэффициентов целесообразно использовать для распространения данных выборочного наблюдения в случаях, если его результаты значительно уступают в точности данным статистической отчетности или точность собранного статистического материала вызывает сомнение.
МАЛАЯ ВЫБОРКА
В процессе оценки степени представительности данных выборочного наблюдения важное значение приобретает вопрос об объеме выборочной совокупности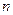 
.
От него зависит не только величина пределов, которые с данной вероятностью не превзойдет ошибка выборки, но и способы определения этих пределов.
При большом числе единиц выборочной совокупности (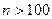 
) распределение случайных ошибок выборочной средней в соответствии с теоремой Ляпунова нормально или приближается к нормальному по мере увеличения числа наблюдений.
Вероятность выхода ошибки за определенные пределы оценивается на основе таблиц интеграла Лапласа. Расчет ошибки выборки базируется на величине генеральной дисперсии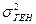 
, так как при больших 
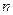коэффициент 
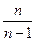, на который для получения генеральной умножается выборочная дисперсия, большой роли не играет.
В практике статистического исследования часто приходится сталкиваться с небольшими по объему так называемыми малыми выборками.
Пример
Предположим, что выборочное обследование 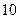рабочих малого предприятия показало, что на выполнение одной из производственных операций рабочие затрачивали времени (мин.): 
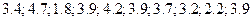. Найдем выборочные средние затраты:
.
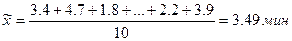Выборочная дисперсия
.
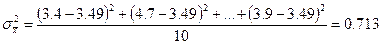Отсюда средняя ошибка малой выборки
.
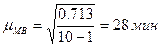По табл. 3.1 находим, что для коэффициента доверия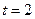 
и объема малой выборки 
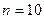вероятность равна 
.
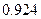Таким образом, с вероятностью 
можно утверждать, что расхождение между выборкой и генеральной средней лежит в пределах от 
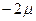до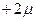 
, т.е. разность 
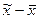не превысит по абсолютной величине ( 
).
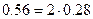Следовательно, средние затраты времени во всей совокупности будут находиться в пределах от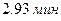 
до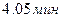 
.
Вероятность того, что это предположение в действительности неверно и ошибка по случайным причинам будет больше, чем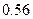 
, равна: 
.
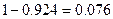Таблица вероятностей Стьюдента часто приводится в иной форме, нежели в табл.3.1. Считается, что в ряде случаев такая форма более удобна для практического использования (табл. 3.2).
Из табл. 3.2 следует, что для каждого числа степеней свободы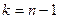 
указана предельная величина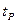 
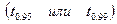, которая с данной вероятностью 
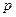не будет превышена в силу случайных колебаний результатов выборки.
На основе указанной в табл. 3.2 величины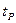 
определяются доверительные интервалы: 
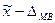и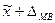 
.
Это область тех значений генеральной средней, выход за пределы которой имеет весьма малую вероятность, равную:
.
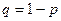В качестве доверительной вероятности при двусторонней проверке используют как правило,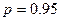 
или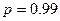 
, что не исключает, однако, выбора и других 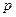, не приведенных в табл. 3.2.
Таблица 3.2
Некоторые значения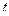 
-распределения Стьюдента
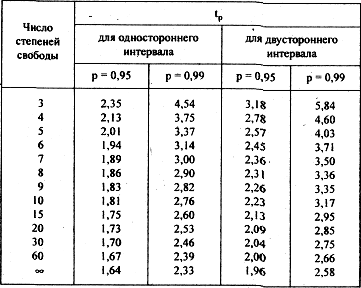
Вероятности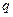 
случайного выхода оцениваемой средней величины за пределы доверительного интервала соответственно будут равны 
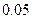и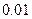 
, т.е. весьма малы.
Выбор между вероятностям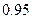и 
и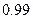 
является до известной степени произвольным. Этот выбор во многом определяется содержанием тех задач, для решения которых применяется малая выборка.
В заключение отметим, что расчет ошибок в малой выборке мало отличается от аналогичных вычислений большой выборке. Различие заключается в том, что при малой выборки вероятность нашего утверждения несколько меньше, чем при больше выборке (в частности, в приведенном ранее примере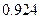 
и 
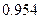соответственно).
Однако все это не означает, что можно использовать малую выборку тогда, когда нужна большая выборка. Во многих случаях расхождения между найденными пределами могут достигать значительных размеров, что вряд ли удовлетворяет исследователей. Поэтому малую выборку следует применять в статистическом исследовании социально-экономических явлений с большой осторожностью, при соответствующем теоретическом и практическом обосновании.
Итак, выводы по результатам малой выборки имеют практическое значение лишь при условии, что распределение признака в генеральной совокупности является нормальным или асимптотически нормальным. Необходимо также принимать во внимание и то, что точность результатов выборки малого объема все же ниже, чем при большой выборке.
Методы математической статистики.
Выборочные наблюдения.
1 Основы теории случайных ошибок и методов оценки случайных погрешностей в измерениях
Анализ случайных погрешностей основывается на теории случайных ошибок, дающей возможность с определенной гарантией вычислить действительное значение измеренной величины и оценить возможные ошибки.
Дата: 2019-02-02, просмотров: 566.
