Алгоритмы. Автоматы. Основные определения. Машина Тьюринга.
Понятие алгоритма
Интуитивно алгоритм можно рассматривать как последовательность действий, которая обладает рядом свойств.
1) Входные данные. Поскольку алгоритм решает некоторую общую
задачу, он обычно получает некоторые инициирующие данные, в
зависимости от которых выполняется.
2) Выходные данные. Любой алгоритм должен давать какой-то результат от своего выполнения.
3) Определенность. В каждый момент времени мы должны точно знать, какое действие выполнить следующим.
4) Элементарность. Это свойство значит, что каждый шаг алгоритма должен быть достататочно прост, чтобы его выполнение не требовало разбиения на меньшие шаги.
5) Конечность. Чтобы выдать результат алгоритм обычно должен
завершить свою работу.
Основные понятия теории автоматов.
Автоматом называется набор 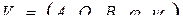 , где
, где
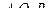 - конечные множества;
- конечные множества;
 – функция, определенная на множестве
– функция, определенная на множестве 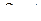 и принимающая значения из
и принимающая значения из 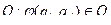 ;
;
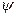 – функция, определенная на множестве
– функция, определенная на множестве 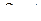 и принимающая значения из
и принимающая значения из 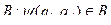 .
.
Множество А – входной алфавит.
Множество В – выходной алфавит.
Множество Q – алфавит состояний.
Функция  – функция переходов.
– функция переходов.
Функция 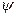 – функция выходов.
– функция выходов.
Входные слова автомата V – произвольная конечная последовательность символов алфавита А.
Выходные слова автомата V – конечная последовательность символов алфавита В.
Л – пустое слово, не имеющее ни одного символа.
Способы задания автоматов.
1. Перечислением элементов множеств 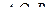 , функции
, функции  и
и 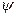 задаются при помощи матриц. Каждая строка сопоставляется символу
задаются при помощи матриц. Каждая строка сопоставляется символу 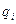 алфавита Q, каждый столбец сопоставляется символу
алфавита Q, каждый столбец сопоставляется символу 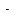 алфавита А. На пересечении строки и столбца содержится символ
алфавита А. На пересечении строки и столбца содержится символ 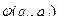 или
или 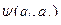 .
.
2. Графический способ получил название диаграммы Мура. На плоскости размещается n кругов, внутри каждого записывается символ 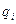 алфавита Q. Рассматриваются всевозможные пары
алфавита Q. Рассматриваются всевозможные пары 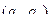 , для каждой пары от круга, в котором записан
, для каждой пары от круга, в котором записан 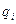 , проводится стрелка к кругу, в котором записан символ
, проводится стрелка к кругу, в котором записан символ 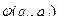 . Этой стрелке приписывается пара
. Этой стрелке приписывается пара 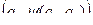 . Из каждого круга выходит ровно m стрелок, где m – количество символов алфавита А.
. Из каждого круга выходит ровно m стрелок, где m – количество символов алфавита А.
Машина Тьюринга.
Машина Тьюринга – гипотетическая модель машина, которая является знакоперерабатывающей функцией.
Машина Тьюринга имеет 3 алфавита:
1. внешний алфавит с пустым символом (в роли данных – слова в некотором конечном алфавите 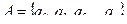 – внешнем алфавите);
– внешнем алфавите);
2. внутренний алфавит, или алфавит состояний 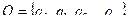 . Состояние
. Состояние  называется заключительным,
называется заключительным, 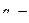 начальным, а состояния
начальным, а состояния  – рабочими состояниями.
– рабочими состояниями.
3. Алфавит сдвигов 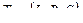 .
.
В конструкции машины имеются:
1) бесконечная лента (разбитая на ячейки), предназначенная для размещения бесконечных записей конечных слов над алфавитом А. В каждой ячейке м.б. записан 1 из символов алфавита А. Пустая ячейка – такая ячейка, в которую помещен некоторый фиксированный символ 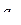 (пробел, ноль,…). Следовательно, в каждый данный момент времени лента полностью заполнена.
(пробел, ноль,…). Следовательно, в каждый данный момент времени лента полностью заполнена.
2) механизм – считывающе-записывающее устройство (СЗУ), называемое также читающей/пишущей головкой. СЗУ обладает способностью обозревать одну ячейку ленты, считывать букву, записанную в ячейке, заносить на место считываемой любую другую букву внешнего алфавита; за один такт работы головка может переместиться на 1 ячейку вправо (R) или на 1 ячейку влево (L) и воспринимать новую ячейку или остаться на месте (S).
3) устройство управления (УУ), которое управляет с помощью программы работой машины.
4) программа машины, определяющая переходы машины от одной конфигурации к другой.

Правила работы машины (правила обращения УУ с программой и СЗУ )
Машина работает дискретно (пошагово). На каждом шаге происходит переход от одной конфигурации к другой.
Перед налом работы машина находится в начальной конфигурации: СЗУ обозревает первую букву слова, а машина находится в начальном состоянии  . СЗУ считывает букву, находящуюся в обозреваемой ячейке. УУ обращается к программе машины: находит клетку, соответствующую считанной букве и состоянию машины. Пусть в этой клетке находится тройка
. СЗУ считывает букву, находящуюся в обозреваемой ячейке. УУ обращается к программе машины: находит клетку, соответствующую считанной букве и состоянию машины. Пусть в этой клетке находится тройка 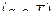 , тогда буква а заносится обозреваемую ячейку, машина переводится в состояние q, а СЗУ совершает сдвиг на 1 ячейку влево, если
, тогда буква а заносится обозреваемую ячейку, машина переводится в состояние q, а СЗУ совершает сдвиг на 1 ячейку влево, если 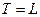 , вправо – при
, вправо – при 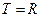 , и остается на месте, если
, и остается на месте, если 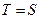 . На этом завершена работа машины на первом шаге и она готова к выполнению следующего аналогичного шага. Работа машины продолжается до тех пор, пока на каком-то из шагов машины не придет в состояние
. На этом завершена работа машины на первом шаге и она готова к выполнению следующего аналогичного шага. Работа машины продолжается до тех пор, пока на каком-то из шагов машины не придет в состояние  . УУ в этом случае останавливает машину. Возникшая конфигурация называется заключительной, а полученное слово – результатом применения машины к исходному слову.
. УУ в этом случае останавливает машину. Возникшая конфигурация называется заключительной, а полученное слово – результатом применения машины к исходному слову.
Итак, правила работы машины: 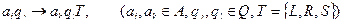 : если машина находится в состоянии
: если машина находится в состоянии 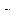 , головка обозревает ячейку, в которой записан символ
, головка обозревает ячейку, в которой записан символ 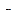 . Символ
. Символ 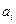 заменяется на
заменяется на  , после этого головка делает движение Т и переходит в состояние
, после этого головка делает движение Т и переходит в состояние 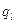 .
.
Если u – исходное слово, Т – машина, то через Т( u) обозначают результат.
Говорят, что МТ неприменима к слову u, если в процессе применения ее к слову она ни на каком из шагов не приходит в заключительное состояние.
Рассмотрим функции: 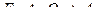 ,
, 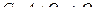 ,
,  .
.
F – функция выхода
G – функция входа
D – функция движения головки.
С использованием этих функций программу для МТ можно представить в виде списка, элементы которого – последовательности вида: 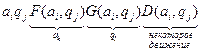 .
.
2) каждому элементу 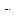 из множества состояний поставим в соответствие вершину, помеченную этим символом. Если есть команда:
из множества состояний поставим в соответствие вершину, помеченную этим символом. Если есть команда: 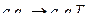 то из вершины
то из вершины  в
в 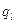 направим ориентированное ребро с меткой
направим ориентированное ребро с меткой 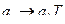 . Тогда программе МТ будет поставлен в соответствие связный ориентированный мультиграф с помеченными ребрами. Он называется диаграммой состояний МТ.
. Тогда программе МТ будет поставлен в соответствие связный ориентированный мультиграф с помеченными ребрами. Он называется диаграммой состояний МТ.
 .
.
Последующее поведение МТ (с некоторого момента времени) полностью определено, если известно:
· состояние МТ в данный момент времени;
· слово, написанное на ленте в данный момент времени;
· положение головки в данный момент времени.
Конфигурация МТ – слово вида 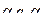 , где
, где 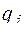 – состояние МТ,
– состояние МТ, 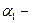 слово, записанное на ленте слева от положения, занятого головкой,
слово, записанное на ленте слева от положения, занятого головкой, 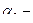 слово, записанное на ленте справа от
слово, записанное на ленте справа от  .
.
Выделяется начальная конфигурация  и конечная:
и конечная:  .
.
Если есть 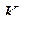 и
и 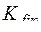 , говорят, что данная МТ применима к входному слову
, говорят, что данная МТ применима к входному слову 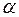 .
.
Если последовательность конфигураций бесконечна, то МТ неприменима к входному слову.
Способы задания МТ
1. Совокупностью команд. Чтобы записать совокупность команд, нужно воспользоваться следующими правилами:
1) начальному шагу алгоритма ставится в соответствие  – начальное состояние;
– начальное состояние;
2) циклы реализуются так, что последнее действие цикла должно соответствовать переходу в то состояние, которое соответствует началу цикла;
3) соседним шагам алгоритма соответствует переход в смежные состояния, которые соответствуют этим пунктам;
4) последний шаг алгоритма вызывает переход в заключительное состояние.
Пример: Пусть алфавит МТ задан множеством A={0, 1, ε}, где символ ε соответствует пустой ячейке, а число состояний устройства управления задано в виде множества Q = {q0, q1, qz}. Если, например, начальная конфигурация имеет вид q0110011, то конечная конфигурация после завершения операции инвертирования должна иметь вид qz001100. Для решения задачи машиной будет порождена следующая последовательность команд:
q01 → q00R, q10 → q10L, q00 → q01R, q11 → q11L, q0 ε → q1εL, q1ε → qzεR.
В стандартной начальной конфигурации головка стоит над первым символом слева, и устройство управления находится в начальном состоянии. На следующем такте машина Тьюринга, не меняя своего состояния, заменяет символ 0 на 1 или 1 на 0 и сдвигается вправо на один символ. После просмотра всей цепочки под головкой оказывается символ, указывающий на пустую ячейку. В этом случае машина Тьюринга переходит в новое состояние и сдвигается влево на один символ. На последующих тактах управляющее устройство не меняет своего состояния, оставляет без изменения символ под головкой и перемещается влево до тех пор, пока не встретит пустую ячейку. Встретив пустую ячейку, машина Тьюринга переходит в заключительное состояние и перемещается вправо на один символ, переходя в стандартную заключительную конфигурацию.
2. Графически. При представлении машины Тьюринга посредством графа необходимо каждому состоянию поставить в соответствие вершину графа, а каждой команде - помеченную дугу. Начальная и конечная вершины графа обычно выделяются; на рисунке они отмечены черным кружком. Если на очередном такте работы машины Тьюринга символ на ленте не изменяется, то в правой части команды его можно не писать (ε на ребре в состояние  ).
).
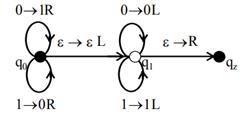
Рисунок 21– Задание МТ графом
3. Таблицей соответсвия (функциональной схемой). При представлении машины Тьюринга данным способом составляется таблица, в которой каждому состоянию соответствует строка, а каждому символу из входного алфавита - столбец. В клетках таблицы на пересечении строки и столбца будет находиться действие (или правая часть команды). Таблица соответствия для задания машины Тьюринга из рассмотренного примера будет выглядеть следующим образом:
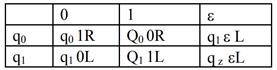
Примеры выполнения типовых заданий.
Пример №1. Дан автомат с диаграммой Мура. Составить таблицы функций. Для данного входного слова 0110100 найти выходное слово.
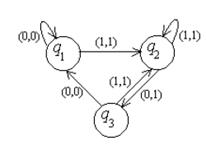
Строим таблицы функций:

Если  , то по диаграмме определяем, что
, то по диаграмме определяем, что  , если
, если  , то
, то
 и т.д.
и т.д.
Пусть дано входное слово 0110100. Найдем выходное слово:
1 шаг.  ,
,  ,
,  .
.
2 шаг.  ,
,  ,
,  .
.
3 шаг.  ,
,  ,
,  .
.
4 шаг.  ,
, 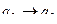 ,
,  .
.
5 шаг.  ,
, 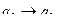 ,
,  .
.
6 шаг. 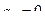 ,
, 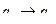 ,
,  .
.
7 шаг. 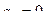 ,
, 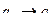 ,
,  .
.
Получаем выходное слово: 0111110.
Пример № 2. Дана машина Тьюринга с внешним алфавитом А = {a0, 1, * }, алфавитом внутренних состояний Q = {q0, q1, q2, q3}, и следующей функциональной схемой:

Задать для нее граф. Применить машину Тьюринга к слову a=11*1, начиная со стандартного начального положения.
Решение.
Граф будет выглядеть следующим образом:
Заменяем содержимое обозреваемой ячейки 1 на а0, машина переходит в новое состояние q2, головка перемещается влево. Дальнейшие действия представлены пошагово в таблице.

| 
| |
| 2 | 
| 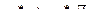
|
| 3 | 
| 
|
| 4 | 
| 
|
| 5 | 
| 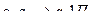
|
| 6 | 
| 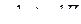
|
| 7 | 
| 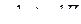
|
| 8 | 
| 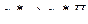
|
| 9 | 
| 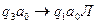
|
| 10 | 
| 
|
| 11 | 
| 
|
 Решение может быть записано в строчку как последовательность конфигураций:
Решение может быть записано в строчку как последовательность конфигураций:

Задания для совместного решения.
 1. Дан автомат с диаграммой Мура. Составить таблицы функций. Для данного входного слова 00111010 найти выходное слово.
1. Дан автомат с диаграммой Мура. Составить таблицы функций. Для данного входного слова 00111010 найти выходное слово.
Ответ: 11011001
2. Применить машину Тьюринга из примера №2 к слову a=1*11, начиная со стандартного начального положения.
Ответ: 111
Индивидуальные контрольные задания.
1. Дан автомат диаграммой Мура (или таблицей). Составить таблицы функций (диаграмму). Для данного входного слова найти выходное слово.
2. Дана МТ последовательностью команд (B – пустая ячейка). Составить граф и таблицу соответствия. Применить машину Тьюринга к данному слову, начиная со стандартного начального положения q1.
| Задание 1 | Задание2 | |||
| диаграмма (таблица) | Входное слово | МТ | Входное слово | |
| 1 | 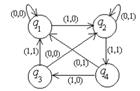
| 01000100 | aq1→aq1R bq1→bq2R Bq1→bq2R aq2→bq3L bq2→aSTOP Bq2→aq3R aq3→aq3L bq3→bq3L Bq3→bq3L | aabba |
| 2 | 
| 11111011 | 0q1→1q1L 1q1→0q2L Bq1→Bq2R 0q2→1q3L 1q2→1STOP Bq2→0q3R 0q3→1q1L 1q3→0q2L Bq3→Bq3L | 011001 |
| 3 | 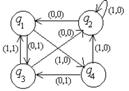
| 11000001 | *q1→1q1R 1q1→*q2L Bq1→Bq2R *q2→1q3R 1q2→1q3L Bq2→*q3R *q3→1q1L 1q3→*STOP Bq3→Bq3R | 11*111 |
| 4 | 
| 00110100 | 0q1→0q1L -q1→-q2R Bq1→Bq2R 0q2→0q3R -q2→0q3L Bq2→-q3L 0q3→0q1R -q3→0STOP Bq3→0q3R | 00--00- |
| 5 | 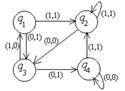
| 10010010 | 1q1→1q1L 2q1→2q2R Bq1→Bq3L 1q2→2STOP 2q2→1q3L Bq2→2q3R 1q3→1q2R 2q3→2q1R Bq3→1q3R | 111221 |
| 6 | 
| 00001110 | 1q1→2q2L 2q1→2q1R Bq1→Bq2L 1q2→2STOP 2q2→1q3L Bq2→2q2R 1q3→1q1L 2q3→2q2R Bq3→1q3R | 111221 |
| 7 | 
| 01110001 | mq1→tq2R tq1→mq3R Bq1→tq2L mq2→BSTOP tq2→tq3L Bq2→mq2L mq3→mq2L tq3→Bq1R Bq3→tq3R | mttmtm |
| 8 | 
| 10001110 | mq1→Bq2R aq1→mq3R Bq1→aq1L mq2→aSTOP aq2→mq3L Bq2→mq2R mq3→aq2L aq3→Bq1R Bq3→aq2R | mamaam |
| 9 | 
| 01111110 | 0q1→Bq3R kq1→kq1R Bq1→kq1L 0q2→0q2R kq2→kq3L Bq2→Bq1L 0q3→Bq2L kq3→0STOP Bq3→kq2R | kk000k |
| 10 | 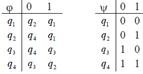
| 10000001 | *q1→+q3R +q1→*q2R Bq1→+STOP *q2→*q2R +q2→+q3L Bq2→+q2R *q3→Bq1L +q3→+q1L Bq3→+q2R | ++**++* |
| 11 | 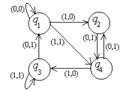
| 00110001 | xq1→xq2R yq1→yq3L Bq1→xq1R xq2→yq1L yq2→Bq2R Bq2→xSTOP xq3→yq1R yq3→yq3L Bq3→xq2L | xxyyxx |
| 12 | 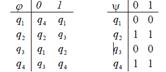
| 11001111 | 0q1→0q2R +q1→0q1R Bq1→+q3R 0q2→+q1L +q2→Bq2R Bq2→+STOP 0q3→0q3L +q3→0q1R Bq3→Bq2R | 00++0+ |
| 13 | 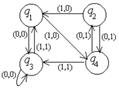
| 10010011 | xq1→xq3L +q1→+q1R Bq1→Bq2L xq2→xq1R +q2→Bq2R Bq2→+q3R xq3→xq1L +q3→+STOP Bq3→+q2L | +++xx+ |
| 14 | 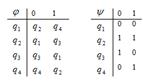
| 00100110 | 0q1→2q2R 2q1→2q2R Bq1→BSTOP 0q2→0q1R 2q2→0q1R Bq2→Bq3L 0q3→0q2R 2q3→2q2L Bq3→0q1L | 002202 |
| 15 | 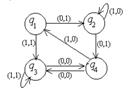
| 00010001 | *q1→1q1L 1q1→*q2R Bq1→Bq2R *q2→1q3R 1q2→1q3L Bq2→*q3L *q3→1q1R 1q3→*STOP Bq3→Bq3R | 1111*1 |
| 16 | 
| 10101100 | 0q1→2q2R 2q1→0q2R Bq1→BSTOP 0q2→0q1R 2q2→0q1R Bq2→Bq3R 0q3→2q2R 2q3→2q2R Bq3→Bq1L | 2202002 |
| 17 | 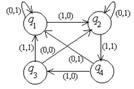
| 00000110 | nq1→nq2L oq1→oq2R Bq1→Bq2R nq2→oq1R oq2→Bq1R Bq2→nq3L nq3→nq2L oq3→BSTOP Bq3→oq1L | oonoon |
| 18 | 
| 11100011 | 0q1→1q3R 1q1→1q2R Bq1→BSTOP 0q2→0q1R 1q2→0q3R Bq2→Bq1L 0q3→0q2R 1q3→1q1L Bq3→0q1R | 110001 |
| 19 | 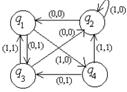
| 00100111 | 0q1→0q1L -q1→-q2R Bq1→Bq2R 0q2→-q3L -q2→0q3L Bq2→-q3L 0q3→-q1R -q3→0STOP Bq3→0q3R | 0-0-0-0-0 |
| 20 | 
| 10101010 | cq1→cq2L uq1→cq1R Bq1→Bq3L cq2→uq1R uq2→Bq3L Bq2→cq2R cq3→cSTOP uq3→uq2L Bq3→uq3R | ccuuuc |
| 21 | 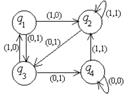
| 01010101 | 1q1→2q2L 2q1→2q3R Bq1→Bq2L 1q2→2STOP 2q2→1q3L Bq2→2q2R 1q3→1q2L 2q3→2q1R Bq3→1q3R | 112211 |
| 22 | 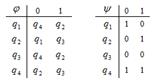
| 01001010 | mq1→tq2L tq1→mq3R Bq1→tq1L mq2→BSTOP tq2→tq3L Bq2→mq2R mq3→mq2L tq3→Bq1L Bq3→tq3R | mmttmt |
| 23 | 
| 00100010 | mq1→Bq3R aq1→mq1R Bq1→aq1L mq2→aq2R aq2→mq3L Bq2→mSTOP mq3→aq2L aq3→Bq1R Bq3→aq2R | amamma |
| 24 | 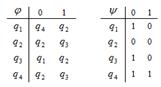
| 11011111 | 0q1→Bq3R kq1→kq2L Bq1→0q1R 0q2→0q2R kq2→kq3L Bq2→Bq2R 0q3→kq1L kq3→0STOP Bq3→kq2R | k0k0k0 |
| 25 | 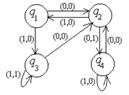
| 00011011 | *q1→+q3L +q1→*q2R Bq1→+STOP *q2→+q1L +q2→+q3R Bq2→*q2L *q3→Bq1L +q3→+q1L Bq3→Bq2R | ***+++ |
| 26 | 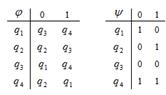
| 11111100 | xq1→xq2R yq1→yq3R Bq1→xq1R xq2→yq1L yq2→Bq2R Bq2→xSTOP xq3→yq1L yq3→Bq3R Bq3→xq2L | xxxyyy |
| 27 | 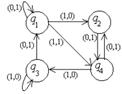
| 01110001 | 0q1→0q2L +q1→Bq3R Bq1→+q2L 0q2→+q1R +q2→Bq2L Bq2→+q2R 0q3→+STOP +q3→0q1L Bq3→0q3R | 0+0++0 |
| 28 | 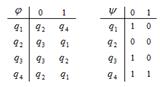
| 01101110 | xq1→+q3L +q1→+q2R Bq1→Bq1L xq2→xq1R +q2→Bq2L Bq2→+q3R xq3→xq1L +q3→xSTOP Bq3→+q2L | x++x+x |
| 29 | 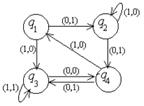
| 11010101 | cq1→cq2L uq1→cq1R Bq1→Bq3L cq2→uq1R uq2→Bq3R Bq2→cq2R cq3→cSTOP uq3→uq2L Bq3→uq3L | uucccu |
| 30 | 
| 01100100 | nq1→nq3L oq1→oq3L Bq1→Bq2L nq2→oq1R oq2→Bq3R Bq2→nq3R nq3→nq2L oq3→oSTOP Bq3→nq2L | onnoon |
Практическая работа №17. Контрольная работа №2 (итоговое тестирование).
Типовой вариант теста.
Вариант 0
| 1. | Какая формула тождественна x « y? | ||||||||||||||||||
А. 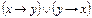
| Б. 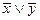
| В. 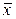 Ú y Ú y
| Г. (x®y)Ù(y®x) | ||||||||||||||||
| 2. | Выбрать операцию алгебры логики, задаваемую таблицей истинности:
| ||||||||||||||||||
А. 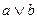
| Б. 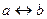
| В. 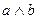
| Г. 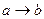
| ||||||||||||||||
| 3. | Выбрать логическую операцию, которая выражена через многочлен Жегалкина: | ||||||||||||||||||
А. 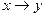
| Б. 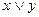
| В. 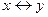
| Г. 
| ||||||||||||||||
| 4 | Представить в виде многочлена Жегалкина | ||||||||||||||||||
А. 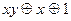
| Б. 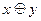
| В. 
| Г. 
| ||||||||||||||||
| 5 | Логическая функция задана таблицей истинности. Найти для нее КНФ.
| ||||||||||||||||||
А. 
| Б. 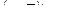
| В. 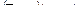
| Г. 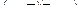
| ||||||||||||||||
| 6 | Логическая функция задана таблицей истинности. Найти для нее ДНФ.
| ||||||||||||||||||
А. 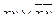
| Б. 
| В. 
| Г. 
| ||||||||||||||||
| 7 | К какому из классов Поста принадлежит функция | ||||||||||||||||||
А. 
| Б. 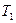
| В.S | Г. ни к одному из перечисленных | ||||||||||||||||
| 8 | Какое из равенств верно? | ||||||||||||||||||
А. x ® y º  Ú y Ú y
| Б. x ® y º x Ú y | В. x ® y º x Ù y | Г. x Û y º x Ú y | ||||||||||||||||
| 9 | Дизъюнкцией двух высказываний х и y называется высказывание… | ||||||||||||||||||
| А. ложное тогда и только тогда, когда оба высказывания х и ложны. | Б. истинное тогда и только тогда, когда истинности высказываний х и y совпадают | В. истинное тогда и только тогда, когда истинны оба высказывания х и y | Г. ложное тогда и только тогда, когда оба высказывания х и y истины. | ||||||||||||||||
| 10 | Найти среди многочленов Жегалкина линейный: | ||||||||||||||||||
А. 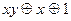
| Б. 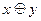
| В. 
| Г. 
| ||||||||||||||||
| 11 | Булевой функцией f (x1, x2, …, xn) называется | ||||||||||||||||||
| А. дизъюнкция простых конъюнкций. | Б. выражения, полученные из переменных x, y,… посредством применения логических операций, а также сами переменные, принимающие значения истинности высказываний | В. произвольная функция, аргументами которой являются логические переменные и принимающая только одно из двух значений: «1» или «0» | Г. формула, равносильная исходной формуле логики высказываний и записанная в виде конъюнкции элементарных дизъюнкций переменных. | ||||||||||||||||
| 12 | Какие переменные в предикате ∀x2∃x5P(x1,x2,x3,x4,x5) являются связными? | ||||||||||||||||||
| А. x1,x2,x3,x4,x5 | Б. x2,x5 | В. x1,x3,x4 | Г. Р | ||||||||||||||||
| 13 | Множеству (А∩В)\С соответствует диаграмма | ||||||||||||||||||
А. 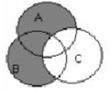
| Б. 
| В. 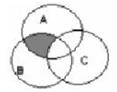
| Г. 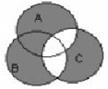
| ||||||||||||||||
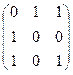
| 14 | Найти граф, соответствующий матрице смежности
| ||||||||||||||||||
А. 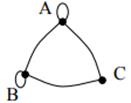
| Б. 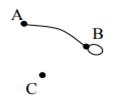
| В. 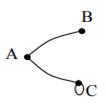
| Г. 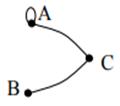
| ||||||||||||||||
| 15 | Если связи между вершинами графа характеризуются определенной ориентацией, то граф называется | ||||||||||||||||||
| А. циклическим | Б. взвешенным | В. конечным | Г. орграфом | ||||||||||||||||
Ответы к тесту:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Г | Г | Г | В | Г | Ф | А | А | А | Б | В | Б | В | В | Г |
Критерии оценивания:
«5» - 14 - 15 правильных ответов
«4» – 11-13 правильных ответов
«3» – 8 -10 правильных ответов
Типовой расчет по курсу «Дискретная математика».
Указания по выполнению типового расчета.
Типовой расчет по математическим дисциплинам выполняется в процессе изучения дисциплин.
Цели и задачи выполнения типового расчета
- Повторение и систематизация изучаемого материала;
- Контроль знаний по различным темам курса;
- Изучение дополнительной литературы и различных источников информации;
- Отработка алгоритмов решения задач;
- Систематизация самостоятельной работы студентов
Алгоритм выполнения типового расчета
Определение варианта работы. Вариант типового расчета определяется согласно порядковому номеру в списке группы по таблице.
- Получение заданий типового расчета.
- Определение списка тем, по которым выполняется типовой расчет.
- Подготовка литературы по необходимым темам.
- Изучение учебной литературы, повторение алгоритмов решения задач, оформления решения.
- Выполнение заданий в черновом варианте, консультация преподавателя.
- Оформление типового расчета, титульного листа.
- Сдача типового расчета на проверку преподавателю.
- Защита типового расчета.
- Доработка недоделок, исправление ошибок, вторичная защита.
Требования к оформлению типового расчета
- При оформлении типового расчета необходимо оформить титульный лист
- Тексты заданий переписываются полностью.
- Решение задач должно быть подробным, развернутым, с необходимыми пояснениями, ссылками на теоретический материал.
- В конце каждого задания должен быть выписан ответ.
- В конце работы должен быть указан список литературы в соответствие с требованиями по оформлению.
Требования при защите типового расчета
- При защите типового расчета студенту могут быть заданы уточняющие вопросы по теоретическому материалу, который применяется в данном расчете.
- При необходимости студент может получить задания, аналогичные тем, которые выполнялись в типовом расчете;
- Студент должен уметь пояснить решение задач, знать определения, теоремы и алгоритмы решения.
Критерии оценивания типового расчета
При оценивании типового расчета учитываются:
- Правильность решения заданий
- Обоснование решение
- Правильность и аккуратность оформления
- Использование дополнительных знаний по предмету
- Исполнительная дисциплина (своевременность сдачи)
- Качество защиты типового расчета (ответы на вопросы, решение заданий)
Типовые задания.
- Докажите тождество используя:
а. определение операций над множествами;
б. с помощью алгебры логики
в. с помощью диаграмм Эйлера.
2. Бинарное отношение Р задано на множестве В = { 1, 2, 3, 4}, Р Í В2. Изобразите Р графически и с помощью матрицы бинарного отношения. Проверьте с помощью матрицы, является ли это отношение рефлексивным, симметричным, транзитивным.
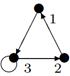
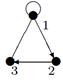
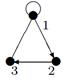
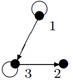
- Даны графы G 1 и G 2. Найдите G 1 Ç G 2 , G 1 È G 2. Для графа G 1 È G 2 найдите матрицы смежности, инцидентности.
- Найдите радиус и диаметр графа. Является ли этот граф эйлеровым?
- Составьте таблицу истинности для формулы.
- Проверьте, являются ли данные формулы эквивалентными с помощью
а) таблицы истинности
б) эквивалентных преобразований.
- С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ.
- Найдите сокращенную, все тупиковые и минимальные ДНФ данной булевой функции.
- Является ли полной система функций?
- Дан автомат диаграммой таблицей соответствия. Составить диаграмму Мура. Для данного входного слова найти выходное слово.
Распределение заданий по вариантам.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 | 84 | 94 |
| 5 | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 11 | 1 | 12 | 21 | 32 | 43 | 54 | 65 | 76 | 87 | 98 |
| 12 | 2 | 13 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 |
| 13 | 3 | 14 | 23 | 34 | 45 | 56 | 67 | 78 | 89 | 100 |
| 14 | 4 | 15 | 24 | 35 | 50 | 57 | 68 | 79 | 90 | 91 |
| 15 | 5 | 16 | 25 | 36 | 49 | 58 | 69 | 80 | 89 | 93 |
| 16 | 6 | 17 | 26 | 37 | 48 | 59 | 70 | 78 | 88 | 92 |
| 17 | 7 | 18 | 27 | 38 | 47 | 60 | 62 | 76 | 87 | 94 |
| 18 | 8 | 19 | 28 | 39 | 46 | 59 | 64 | 74 | 85 | 95 |
| 19 | 9 | 20 | 29 | 40 | 41 | 58 | 66 | 72 | 86 | 97 |
| 20 | 10 | 11 | 21 | 32 | 43 | 57 | 68 | 79 | 84 | 94 |
| 21 | 1 | 13 | 22 | 31 | 45 | 56 | 70 | 77 | 83 | 96 |
| 22 | 2 | 14 | 23 | 34 | 47 | 55 | 61 | 75 | 81 | 99 |
| 23 | 3 | 15 | 24 | 33 | 49 | 54 | 63 | 73 | 82 | 100 |
| 24 | 4 | 16 | 25 | 36 | 42 | 53 | 65 | 71 | 90 | 99 |
| 25 | 5 | 17 | 26 | 35 | 44 | 52 | 67 | 80 | 85 | 98 |
| 26 | 6 | 18 | 27 | 37 | 46 | 51 | 69 | 71 | 86 | 96 |
| 27 | 7 | 19 | 28 | 36 | 48 | 52 | 70 | 73 | 81 | 97 |
| 28 | 8 | 20 | 29 | 39 | 50 | 53 | 62 | 74 | 82 | 95 |
| 29 | 9 | 11 | 30 | 38 | 41 | 54 | 65 | 72 | 87 | 91 |
| 30 | 10 | 15 | 21 | 32 | 50 | 59 | 64 | 72 | 85 | 99 |
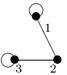
Задание 1

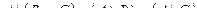
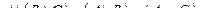
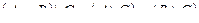
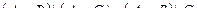
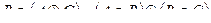
|
Задание 2 | |
| 11 | (1;1) (2;1) (2;2) (2;3) (2;4) (3;3) (4;4) |
| 12 | (1;1) (1;4) (2;2) (2;3) (3;3) (3;2) (4;1) (4;4) |
| 13 | (2;1) (3;1) (3;2) (4;1) (4;3) |
| 14 | (1;1) (1;2) (2;2) (3;3) (4;3) (4;4) |
| 15 | (1;1) (2;4) (2;1) (3;3) (4;2) (4;1) |
| 16 | (1;1) (1;4) (2;1) (3;4) (4;3) (4;1) |
| 17 | (1;3) (1;4) (2;2) (3;3) (4;3) (4;4) |
| 18 | (1;3) (1;2) (2;3) (3;2) (3;4) (4;1) |
| 19 | (1;1) (1;2) (2;2) (3;3) (4;1) (4;4) |
| 20 | (1;1) (1;3) (2;4) (3;1) (3;4) (4;3) (4;2) |
|
Задание 3 | |||||

| 
| 
| 
| ||
| 21 | 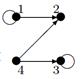
| 
| 26 | 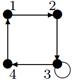
| 
|
| 22 | 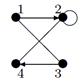
| 
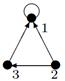
| 27 | 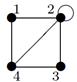
| 
|
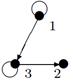
| 23 | 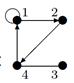
| 
| 28 | 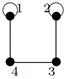
| 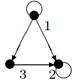
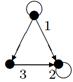
|
| 24 | 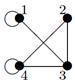
| 
| 29 | 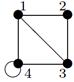
| 
|
| 25 | 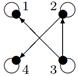
| 
| 30 | 
| 
|
|
Задание 4 | |||
| 31 | 
| 36 | 
|
| 32 | 
| 37 | 
|
| 33 | 
| 38 | 
|
| 34 | 
| 39 | 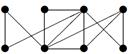
|
| 35 | 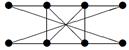
| 40 | 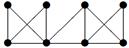
|
|
Задание 5 | |||
| 41 | 
| 46 | 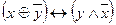
|
| 42 | 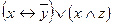
| 47 | 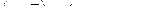
|
| 43 | 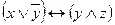
| 48 | 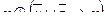
|
| 44 | 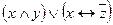
| 49 | 
|
| 45 | 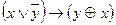
| 50 | 
|
|
Задание 6 | |||||
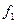
| 
| 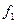
| 
| ||
| 51 | 
| 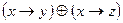
| 56 | 
| 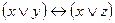
|
| 52 | 
| 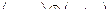
| 57 | 
| 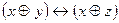
|
| 53 | 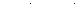
| 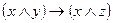
| 58 | 
| 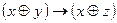
|
| 54 | 
| 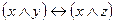
| 59 | 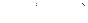
| 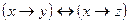
|
| 55 | 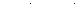
| 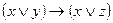
| 60 | 
| 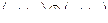
|
|
Задание 7 | |||
| 61 | 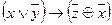
| 66 | 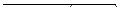
|
| 62 | 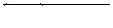
| 67 | 
|
| 63 | 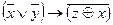
| 68 | 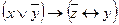
|
| 64 | 
| 69 | 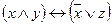
|
| 65 | 
| 70 | 
|
|
Задание 8 | |||
| 71 | 
| 76 | 
|
| 72 | 
| 77 | 
|
| 73 | 
| 78 | 
|
| 74 | 
| 79 | 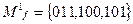
|
| 75 | 
| 80 | 
|
|
Задание 9 | |||||
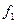
| 
| 
| 
| ||
| 81 | 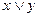
| 
| 86 | 
| 
|
| 82 | 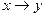
| 
| 87 | 
| 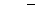
|
| 83 | 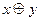
| 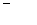
| 88 | 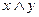
| 
|
| 84 | 
| 
| 89 | 
| 
|
| 85 | 
| 
| 90 | 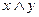
| 
|
|
Задание 10 | |||||
| 91 | 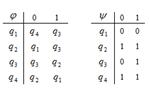
| 11000001 | 96 | 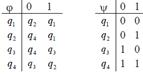
| 11111100 |
| 92 | 
| 00110100 | 97 | 
| 01110001 |
| 93 | 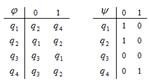
| 10010010 | 98 | 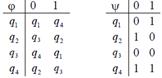
| 01101110 |
| 94 | 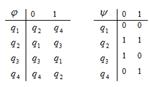
| 00001110 | 99 | 
| 11010101 |
| 95 | 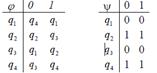
| 01110001 | 100 | 
| 01100100 |
Список используемых источников
1. Артюхина Д.Д. Элементы математической логики: учебное пособие. – Старый Оскол: СТИ НИТУ «МИСиС», 2016. – 160 с.
2. Балюкевич Э.Л., Ковалева Л.Ф., Романников А.Н. Дискретная математика: Учебное пособие, руководство по изучению дисциплины / Московский государственный университет экономики, статистики и информатики, – М., 2007. – 125 с.
3. Дискретная математика. Алгебра логики (Алгебра высказываний): метод, указания к выполнению самостоят, и контрол. работы / сост. Л.В. Балабко. – Архангельск: Изд-во ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М.В. Ломоносова», 2011. – 42 с.
4. Дискретная математика: практикум / сост. И.А, Сурикова; Яросл. гос. ун-т им. П.Г.Демидова. – Ярославль: ЯрГУ, 2010. – 76 с.
5. Игошин В.И. Математическая логика и теория алгоритмов: учебное пособие для студ. высш. учеб. заведений – М.: Издательский центр «Академия», 2014. – 448 с.
6. Математическая логика. Типовые расчёты: методические указания и контрольные задания / сост.: Е.С. Лоскутова, А.Д. Нахман. – Тамбов: Изд-во Тамб. гос. техн. ун-та, 2008. – 28 с.
7. Новиков Ф.А. Дискретная математика для программистов: учебник для вузов. СПб.: Питер, 2004. – 364 с.
8. Судоплатов С.В., Овчинников Е.В. Элементы дискретной математики: учебник. М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002. – 280 с.
9. Усов С.В.Дискретная математика. Учебно-методическое пособие для студентов направления «Информатика и вычислительная техника». – Омск: ОмГУ, 2011. – 60 с.
Дата: 2018-12-28, просмотров: 420.
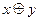
 .
.