Минимизация ДНФ.
ДНФ называется минимальной, если она содержит по сравнению с другими эквивалентными ей формами минимальное количество букв (при подсчете учитывается каждое вхождение буквы в формулу). Элементарную конъюнкцию 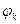 назовем импликантой булевой функции f, если не существует такого двоичного набора переменных, при котором функция
назовем импликантой булевой функции f, если не существует такого двоичного набора переменных, при котором функция 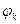 принимает значение 1, а функция f – значение 0, то есть
принимает значение 1, а функция f – значение 0, то есть 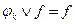 . Элементарная конъюнкция, входящая в ДНФ булевой функции, называется ее простой импликантой, если никакая ее часть не является импликантой этой функции.
. Элементарная конъюнкция, входящая в ДНФ булевой функции, называется ее простой импликантой, если никакая ее часть не является импликантой этой функции.
Сокращенной ДНФ данной булевой функции называется ее ДНФ, составленная только из простых импликант.
Для приведения булевой функции к сокращенной ДНФ используется, так называемое правило склеивания:  .
.
Часто используется неполное склеивание, при котором оба члена, участвовавших в склеивании (или один из них), могут повторно склеиваться с другими оставшимися членами СДНФ. Процесс многоступенчатого склеивания приводит к импликантам, которые не склеиваются с другими. Такие импликанты называют простыми. Форма записи булевой функции в ДНФ, состоящая только из простых импликант, называется сокращенной дизъюнктивной нормальной формой (Сокр ДНФ).
Для любой заданной функции сокращенная ДНФ является единственной. Однако она может быть избыточной вследствие того, что некоторые простые импликанты этой суммы покрываются совокупностями других слагаемых. Такие импликанты называют лишними, и они могут быть удалены без нарушения равносильности формул.
Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой ДНФ.
Теорема. Если в СДНФ функции алгебры логики произвести всевозможные операции неполного склеивания, а затем всевозможные операции элементарного поглощения, то полученная форма функции будет сокращенной.
Для нахождения МДНФ используются различные методы. Ниже будут приведены метод Квайна, геометрический метод и метод Карно.
Метод Квайна основывается на применении двух основных соотношений: склеивании и поглощении. Заключается он в выполнении следующих шагов:
1. Записать СДНФ.
2. Произвести все возможные полные и неполные склеивания и поглощения. Получим сокращенную ДНФ.
3. Строится матрица Квайна: строки матрицы – простые импликанты сокращенной ДНФ, столбцы – конъюнкты СДНФ. На пересечении соответствующей строки и столбца ставится метка (*), если простая импликанта входит в соответствующий конъюнкт.
4. Их простых импликант составить МДНФ по следующему правилу.
Импликанты, которые не могут быть лишними и, следовательно, не могут быть исключены из сокращенной формы, составляют ядро. Входящие в ядро импликанты легко определяются по импликантной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только данной импликантой. Для получения минимальной формы достаточно выбрать из импликант, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждой из этих импликант, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра.
Геометрический метод основан на представлении булевой функции единичным n-мерным кубом. Напомним, что для любой булевой функции существует ее представление в СДНФ. Причём в алгоритме построения СДНФ используются только те наборы значений, при которых функция равна единице. Это позволяет проинтерпретировать геометрическое представление функции следующим образом: любой грани, ребру или вершине можно поставить в соответствие простую импликанту по правилу – в нее войдут переменные, значение которых сохраняется на данном подмножестве куба, причем, если переменная равна 1, то она входит без отрицания, если 0, то с отрицанием.
Пример.
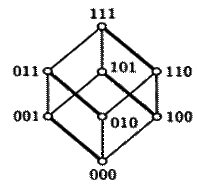
| грани:
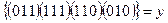
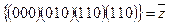 ребра:
ребра:
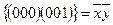
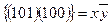 вершины:
вершины:
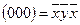
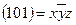
|
Алгоритм геометрического метода:
1. Задать булеву функцию единичным n-мерным кубом.
2. Составить все интервалы куба: грани, ребра, вершины покрытые * (записывать именно в такой последовательности).
3. Выписать тупиковые интервалы – интервалы, содержащие вершины (вершину), входящие только в данный интервал.
4. Записать из полученных тупиковых интервалов ядро.
5. Если в ядро входят не все вершины, отмеченные *, то добавляя к нему по одному, по два и т.д. неядровые интервалы найти все МДНФ.
Метод Карно – графический способ минимизации булевых функций, обеспечивающий относительную простоту работы с большими выражениями.
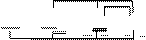
Куб разворачивается на плоскость как показано на рисунке 2 (происходит разрыв горизонтальных ребер передней грани). Таким образом, появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов в таблице
(00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой (рисунок 2).
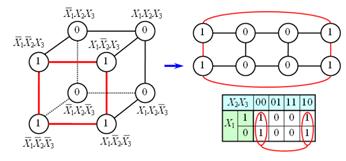
Рисунок 2 – Представление единичного куба картами Карно.
На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в карте рассматриваем только те клетки, которые содержат единицы. Нахождение простых импликант сводится к выделению максимальных по включению прямоугольников, состоящих из единиц. Из прямоугольников, соответствующих граням максимальной размерности, находим коды максимальных интервалов. Считается, что каждая клетка таблицы является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали.
Примеры выполнения типовых заданий.
Пример №1. Найти МДНФ для функции, заданной СДНФ методом Квайна:
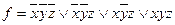 .
.
Решение.
1.  Произведем неполное склеивание. Первый конъюнкт склеивается со вторым, второй с третьим, третий с четвертым.
Произведем неполное склеивание. Первый конъюнкт склеивается со вторым, второй с третьим, третий с четвертым.
2. 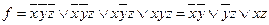 – сокращенная ДНФ.
– сокращенная ДНФ.
2. Строим матрицу Квайна:
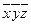
| 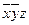
| 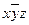
| 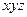
| |
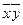
| * | * | ||
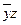
| * | * | ||
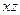
| * | * |
Ядро 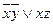 - содержит * во всех столбцах матрицы.
- содержит * во всех столбцах матрицы.
Ответ: МДНФ 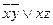 .
.
Пример №2. Найти МДНФ для функции, заданной СДНФ методом Квайна:
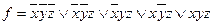 .
.
Решение.
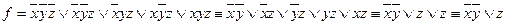 .
.
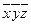
| 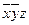
| 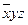
| 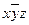
| 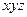
| |
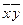
| * | * | |||
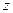
| * | * | * | * |
Ядро: 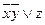 содержит * во всех столбцах матрицы.
содержит * во всех столбцах матрицы.
Ответ: МДНФ 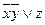 .
.
Пример №3. Найти МДНФ для функции, заданной СДНФ методом Квайна:
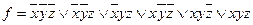 .
.
Решение.
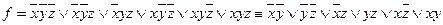 .
.
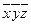
| 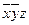
| 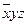
| 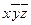
| 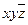
| 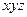
| |
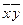
| * | * | ||||
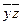
| * | * | ||||
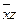
| * | * | ||||
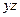
| * | * | ||||
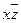
| * | * | ||||
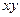
| * | * |
В каждом столбце стоит по 2 *, значит, у функции нет ядра. Тогда будем составлять все возможные пары, тройки, четверки и т.д. дизъюнкции простых импликант, проверяя покрытие столбиков *. Получим два ответа.
Ответ: МДНФ 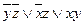
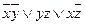
Пример №4. Найти МДНФ для функции геометрическим методом: (11010101)
Решение.
Изобразим единичный куб. Построим таблицу истинности:
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Получим куб:
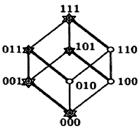
Ему соответствуют интервалы: 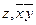 (грань и одно ребро).
(грань и одно ребро).
Тогда ядро: 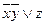 - является МДНФ, так как задействованы все вершины, помеченные *.
- является МДНФ, так как задействованы все вершины, помеченные *.
Ответ: МДНФ 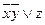 .
.
Пример №5. Найти МДНФ для функции геометрическим методом: (11001011)
Решение.
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
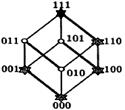 Интервалы:
Интервалы: 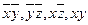
Ядро: 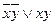
Ядро содержит не все вершины, отмеченные *, будем добавлять к нему по одному, по два и т.д. неядровые интервалы, пока не получим полное покрытие.
Ответ: МДНФ 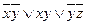 ,
, 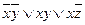
Пример №6. Найти МДНФ для функции методом Карно: (11010101)
Решение.
Исходная функция зависит от трех переменных, таблицу истинности
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
можно представить виде:
| yz x |  00 00
|  01 01
| 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
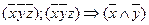
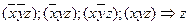
Ответ: МДНФ: 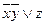 .
.
Пример №7. Найти МДНФ для функции методом Карно: (11001011)
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| yz x |   00 00
| 01 | 11 | 10 | 00 |
| 0 | 1 | 1 | 0 |  0 0
| 1 |
| 1 | 1 | 0 |  1 1
| 1 | 1 |
Интервалы: 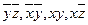
Ответ: МДНФ 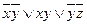 ,
, 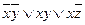
Задания для совместного решения.
Найти МДНФ для заданных функций методом Квайна, геометрическим методом и методом Карно.
| Ответы: | |||
| 1 | (10010110) | 1 | 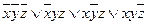
|
| 2 | (00110010) | 2 | 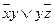
|
| 3 | (11001100) | 3 | 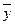
|
| 4 | (10101101) | 4 | 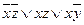
|
| 5 | (01010010) | 5 | 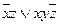
|
Индивидуальные контрольные задания.
Найти МДНФ для заданных функций методом Квайна, геометрическим методом и методом Карно.
| Вариант | f | Вариант | f | Вариант | f |
| 1 | 00011001 | 11 | 01010101 | 21 | 00110001 |
| 2 | 01100100 | 12 | 10101010 | 22 | 10000001 |
| 3 | 01000100 | 13 | 00100111 | 23 | 01111110 |
| 4 | 01101110 | 14 | 11100011 | 24 | 10001110 |
| 5 | 01110001 | 15 | 00000110 | 25 | 01110001 |
| 6 | 11111100 | 16 | 10101100 | 26 | 00001110 |
| 7 | 00011011 | 17 | 00010001 | 27 | 10010010 |
| 8 | 11011111 | 18 | 00100110 | 28 | 00110100 |
| 9 | 00100010 | 19 | 11001111 | 29 | 11000001 |
| 10 | 01001010 | 20 | 10010011 | 30 | 11111011 |
Практическая работа №6. Построение и оптимизация РКС
Дата: 2018-12-28, просмотров: 418.