Общие понятия теории множеств. Способы задания. Основные операции над множествами и их свойства. Мощность множеств. Графическое изображение множеств на диаграммах Эйлера-Венна. Декартово произведение множеств.
Для множества не существует формального определения, считается, что это понятие первичное и не определяется. Говорят, что множество есть объединение различных объектов. Однако, понятие “объединение” и “объекты” остаются неопределяемыми.
Объекты, образующие множество, называются его элементами. Если элемент m принадлежит множеству S, то используют запись m Î S, в противном случае – запись m Ï S.
Множество, содержащее конечное число элементов, называется конечным. Если же множество не содержит ни одного элемента, то оно называется пустым и обозначается Æ.
Множество M называется подмножеством множества S (обозначение МÌS либо SÉМ; читается М входит в S, S содержит М) тогда и только тогда, когда любой элемент множества М принадлежит множеству S.
Число элементов конечного множества S называется его мощностью и обозначается | S|.
Понятие равенства двух множеств: Два множества называются равными, если эти множества содержат одинаковые элементы: AÍB и BÍA ÞA=B
Если AÌB и A¹B – то B – строгое подмножество множества А.
Способы задания множеств:
- перечислением элементов: Конечное множество S будем задавать списком его элементов: S={s1,s2,…,sn}, где s1,s2,…,sn – элементы S (обязательно различные).
- порождающей процедурой: ={1,2,4,8,…;
- описанием свойств его элементов: M={x|P(x)} – какое-то множество значений x, обладающих свойствами P(x).
Операции над множествами.
Объединением множеств А и В называется множество С, элементы которого принадлежат хотя бы одному из множеств А и В.
Обозначается С = А È В.
Тогда AÈB={x|xÎA или xÎB}
Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Венна.
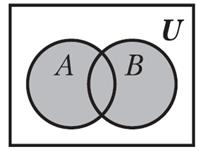
Рисунок 4 – Изображение объединений двух множеств на диаграмме Эйлера-Венна
Пересечением множеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.
Обозначение С = А Ç В.
AÇB={x|xÎA и xÎB}
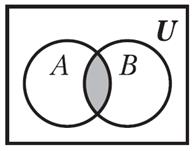
Рисунок 5 – Изображение пересечений двух множеств на диаграмме Эйлера-Венна
Разностью множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.
Обозначается С = А \ В.
A\B={x|xÎA и xÏB}
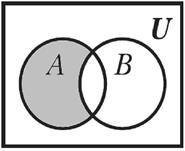
Рисунок 6 – Изображение разности двух множеств на диаграмме Эйлера-Венна
Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В.
Обозначение С=А  В.
В.
A 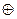 B={x|xÎA и xÏB} или {x|xÎB и xÏA}=A\BÈB\A
B={x|xÎA и xÏB} или {x|xÎB и xÏA}=A\BÈB\A
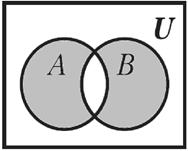
Рисунок 7 – Изображение симметрической разности двух множеств на диаграмме Эйлера-Венна
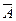 называется дополнением множества А относительно множества U, если А Í U и
называется дополнением множества А относительно множества U, если А Í U и
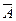 = U \ A.
= U \ A.
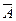 ={x|xÎA и xÎU}, где U – универсальное множество.
={x|xÎA и xÎU}, где U – универсальное множество.
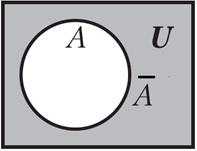
Рисунок 8 – Изображение дополнения множества на диаграмме Эйлера-Венна
Для множеств А, В и С справедливы следующие свойства:
1. А Ç А = А È А = А;
2. A È B = B È A; A Ç B = B Ç A;
3. (A Ç B) Ç C = A Ç (B Ç C); (A È B) È C = A È (B È C);
4. A È (B Ç C) = (A È B) Ç (A È C); A Ç (B È C) = (A Ç B) È (A Ç C);
5. A È (A Ç B) = A; A Ç (A È B) = A;
6. 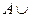 Æ = А; A Ç Æ = Æ;
Æ = А; A Ç Æ = Æ;
7. A È 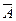 = E; A Ç
= E; A Ç 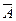 = Æ;
= Æ; 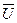 = Æ;
= Æ; 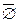 = U;
= U; 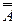 = A;
= A;
8. A \ B Í A; A \ A = Æ; A \ (A \ B) = A Ç B;
9. 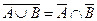 ;
; 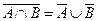
10. A \ B= 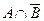 .
.
Соответствие теоретико-множественных операций логическим операциям.
| Название операции | Соответствие в алгебре логики |
| Дополнение | Отрицание 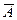
|
| Объединение | Дизъюнкция 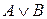
|
| Пересечение | Конъюнкция 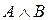
|
| Разность | Конъюнкция 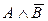
|
| Симметрическая разность | Кольцевая сумма 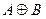
|
| Универсум | 1 |
| Пустое множество | 0 |
Прямым декартовым произведением двух множеств А и В называется множество всех пар (a;b), таких, что аÎА, bÎB. Обозначается А´В.
Если А=В то С=А2.
Декартовым произведением n множеств называется множество 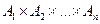 векторов ( a1,… an) таких, что
векторов ( a1,… an) таких, что 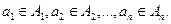
Если 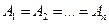 , то
, то 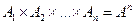
Примеры выполнения типовых заданий.
Пример №1. Проверить равенство двух множеств тремя способами:
а) по определению
б) диаграммами Эйлера-Венна
в) с помощью формул алгебры логики
A \ (B È C) = (A \ B) Ç (A \ C).
Решение.
а) По определению следует, что если некоторый элемент х Î А \ (В È С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.
Множество A \ B представляет собой множество элементов множества А, не принадлежащих множеству В.
Множество А \ С представляет собой множество элементов множества А, не принадлежащих множеству С.
Множество (A \ B) Ç (A \ C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.
Таким образом, тождество можно считать доказанным.
б) На рисунке 9 показано изображение искомого множества левой и правой части равенства: штриховкой показаны промежуточные результаты, результат залит заливкой.
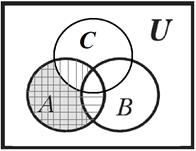
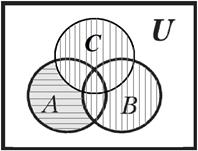
Рисунок 9 – Построение диаграммы Эйлера-Вена
в) Используя соответствие теоретико-множественных операций логическим операциям, упростим левую и правую часть равенства:
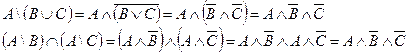
Результаты совпали, значит формула верна.
Пример №2. Заданы подмножества A, B и C множества арабских цифр. Найдите подмножества 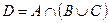 ,
, 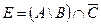 .
.
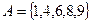 ,
, 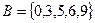 ,
, 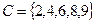 .
.
Решение.
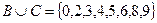 ,
, 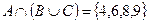 .
.
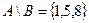 ,
, 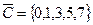 ,
, 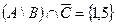
Задания для совместного решения.
1. Проверить равенство двух множеств тремя способами:
- по определению
- диаграммами Эйлера-Венна
- с помощью формул алгебры логики
б. A 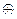 B = (A È B) \ (A Ç B);
B = (A È B) \ (A Ç B);
в. A \ (A \ B) = A Ç B;
г. A Ç (B 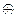 C) = (A Ç B)
C) = (A Ç B) 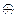 (A Ç C);
(A Ç C);
д. (A \ B) \ C = A \ (B È C).
2. Заданы подмножества A, B и C множества арабских цифр. Найдите подмножества 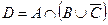 ,
, 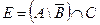 .
.
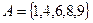 ,
, 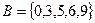 ,
, 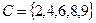 .
.
Индивидуальные контрольные задания.
1. Проверить равенство двух множеств тремя способами:
- по определению
- диаграммами Эйлера-Венна
- с помощью формул алгебры логики
| 1 | 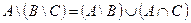
| 16 | 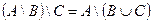
|
| 2 | 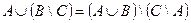
| 17 | 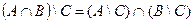
|
| 3 | 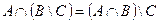
| 18 | 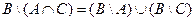
|
| 4 | 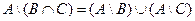
| 19 | 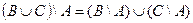
|
| 5 | 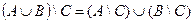
| 20 | 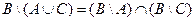
|
| 6 | 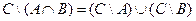
| 21 | 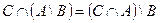
|
| 7 | 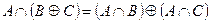
| 22 | 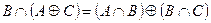
|
| 8 | 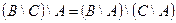
| 23 | 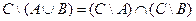
|
| 9 | 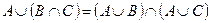
| 24 | 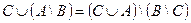
|
| 10 | 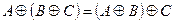
| 25 | 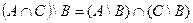
|
| 11 | 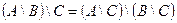
| 26 | 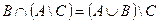
|
| 12 | 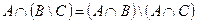
| 27 | 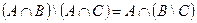
|
| 13 | 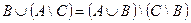
| 28 | 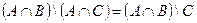
|
| 14 | 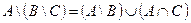
| 29 | 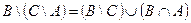
|
| 15 | 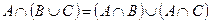
| 30 | 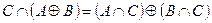
|
2. Заданы подмножества A, B и C множества арабских цифр. Найдите подмножества 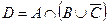 ,
, 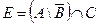 .
.
| 1. | A={1; 2; 3}, | B={1; 5; 6; 7}, | C={0; 4; 8; 9}. |
| 2. | A={0; 2; 7}, | B={1; 3; 5; 7}, | C={0; 2; 3; 8}. |
| 3. | A={1; 2; 7}, | B={1; 3; 5; 7}, | C={0; 2; 3; 7}. |
| 4. | A={1; 5; 8}, | B={1; 3; 5; 9}, | C={0; 2; 3; 7}. |
| 5. | A={1; 5; 8}, | B={1; 3; 6; 7}, | C={0; 3; 4; 8}. |
| 6. | A={1; 2; 3; 5}, | B={1; 3; 5; 7}, | C={1; 2; 5; 8}. |
| 7. | A={1; 2; 3; 5}, | B={1; 3; 5}, | C={1; 2; 5; 8}. |
| 8. | A={1; 2; 3; 5}, | B={1; 3; 7}, | C={1; 2; 5; 9}. |
| 9. | A={1; 2; 3; 5}, | B={3; 5; 7}, | C={1; 2; 5; 6}. |
| 10. | A={1; 2; 3; 5}, | B={1; 5; 8}, | C={1; 3; 5; 8}. |
| 11. | A={1; 2; 3; 5; 9}, | B={1; 3; 5; 7}, | C={5; 8}. |
| 12. | A={1; 2; 3; 5; 8}, | B={1; 3; 5; 8}, | C={5; 8}. |
| 13. | A={1; 2; 3; 5; 9}, | B={1; 3; 5; 7}, | C={5; 9}. |
| 14. | A={1; 2; 3; 7; 9}, | B={1; 3; 5; 7}, | C={8; 9}. |
| 15. | A={0; 2; 3; 5; 9}, | B={1; 2; 6; 7}, | C={7; 9}. |
| 16. | A={0; 2; 3; 5; 9}, | B={1; 2; 7}, | C={2; 3; 6; 7; 9}. |
| 17. | A={0; 2; 4; 5; 9}, | B={1; 2; 6}, | C={2; 3; 4; 7; 8}. |
| 18. | A={0; 2; 3; 5; 9}, | B={1; 2; 7}, | C={0; 3; 5; 6; 9}. |
| 19. | A={0; 2; 3; 5; 9}, | B={1; 2; 8}, | C={0; 3; 5; 6; 8}. |
| 20. | A={0; 2; 3; 4; 6}, | B={1; 2; 7}, | C={0; 4; 5; 6; 7}. |
| 21. | A={0; 2}, | B={1; 2; 7}, | C={0; 3; 5}. |
| 22. | A={0; 2}, | B={1; 2; 5}, | C={0; 4; 5}. |
| 23. | A={1; 2}, | B={1; 2; 3}, | C={0; 3; 5}. |
| 24. | A={1; 2}, | B={0; 2; 4}, | C={0; 3; 4}. |
| 25. | A={0; 3}, | B={1; 2; 3}, | C={0; 3; 5}. |
| 26. | A={0; 2; 3; 5; 9}, | B={1; 2; 7; 8; 9}, | C={0; 3; 5; 6; 9}. |
| 27. | A={1; 2; 4; 5; 7}, | B={1; 2; 7; 8; 9}, | C={0; 3; 5; 6; 9}. |
| 28. | A={1; 2; 4; 5; 7}, | B={1; 3; 6; 8; 9}, | C={0; 3; 5; 6; 8}. |
| 29. | A={1; 3; 4; 5; 7}, | B={1; 3; 6; 8}, | C={2; 3; 5; 6; 7}. |
| 30. | A={0; 3; 4; 6; 7}, | B={1; 3; 6; 7; 9}, | C={0; 2; 5; 6; 8}. |
Практическая работа №11. Исследование свойств бинарных отношений.
Дата: 2018-12-28, просмотров: 531.