Основные понятия теории графов. Виды графов: ориентированные и неориентированные графы.
Способы задания графов. Матрицы смежности и инциденций для графа.
Эйлеровы и гамильтоновы графы. Деревья.
Графом G (в широком понимании) называется любая пара (V,E), где V = 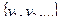 – множество элементов любой природы, а E =
– множество элементов любой природы, а E = 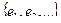 – семейство пар элементов из V, причем допускаются пары вида
– семейство пар элементов из V, причем допускаются пары вида 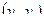 и одинаковые пары.
и одинаковые пары.
Если пары в V рассматриваются как неупорядоченные, то граф называется неориентированным, если как упорядоченные, то граф называется ориентированным (орграфом).
Элементы множества V называются вершинами графа, а пары из E – его ребрами; в орграфе они называются ориентированными ребрами или дугами.
Говорят, что ребро 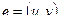 в неориентированном графе соединяет вершины u и v, а в ориентированном графе дуга
в неориентированном графе соединяет вершины u и v, а в ориентированном графе дуга 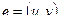 идет из вершины u в вершину v.
идет из вершины u в вершину v.
Говорят, что вершины 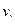 и
и 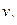 смежны в графе G = (V,E), если в E входит пара
смежны в графе G = (V,E), если в E входит пара 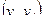 или
или 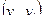 . Говорят, что ребро (дуга)
. Говорят, что ребро (дуга) 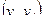 инцидентно вершинам
инцидентно вершинам 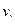 и
и 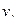 .
.
Способы задания графа.
1. Графический.
Обычно граф представляется диаграммой, на которой вершины изображаются точками, а рёбра – отрезками. На рисунке 11 показаны примеры графического представления неориентированного графа (а) и ориентированного (б).
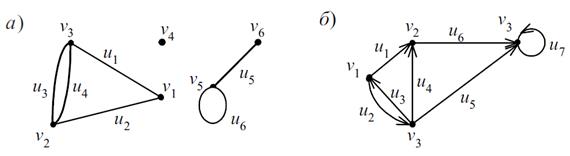
Рисунок 11 – Геометрическое представление графов
Если смежные вершины связаны более, чем одним ребром, то такие дуги называются кратными (на рисунке 11(а) – 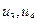 , на рисунке 11(б) –
, на рисунке 11(б) – 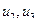 ), а сам граф называется мультиграфом. Вершины, не связанные с другими вершинами, называются изолированными (на рисунке 11(а) –
), а сам граф называется мультиграфом. Вершины, не связанные с другими вершинами, называются изолированными (на рисунке 11(а) – 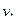 ). Ребро, начинающееся и заканчивающееся в одной точке, называется петлей (на рисунке 11(а) –
). Ребро, начинающееся и заканчивающееся в одной точке, называется петлей (на рисунке 11(а) – 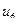 , 11 (б) –
, 11 (б) – 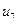 ).
).
2. Матрица смежности.
Матрицей смежности графа D называется квадратичная матрица порядка n, у которой
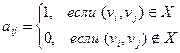
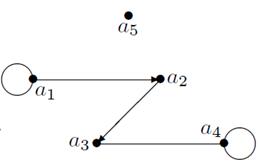
Пример: Для графа, представленного на рисунке, матрица смежности имеет соответствующий вид.
| 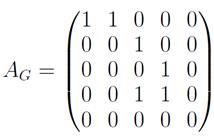
|
Рисунок 12 – Граф и его матрица смежности
Для неориентированного графа матрица смежности симметрична относительно главной диагонали.
3. Матрица инцидентности.
Матрицей инцидентности неорграфа D называется матрица размерности п´т, у которой
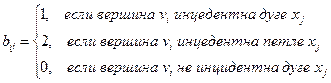
Матрицей инцидентности орграфа D называется матрица размерности п´т, у которой
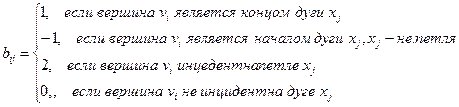
Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij= k, где k – кратность дуги (ребра).
С помощью матриц смежности и инцидентности всегда можно полностью определить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.
Пример. Граф на рисунке имеет матрицу инцидентности:
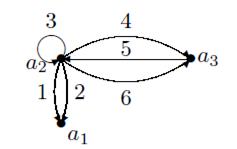
| 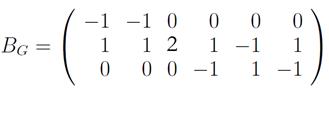
|
Операции с графами.
Граф 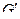 называется подграфом графа G, если множество его вершин есть подмножество вершин графа G, а множество ребер, соединяющих эти вершины сохраняется, и частью графа G, если ребра графа
называется подграфом графа G, если множество его вершин есть подмножество вершин графа G, а множество ребер, соединяющих эти вершины сохраняется, и частью графа G, если ребра графа 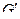 есть подмножество ребер графа G. На рисунке 13 Граф б) есть подграф графа а), а граф в) – часть графа а)
есть подмножество ребер графа G. На рисунке 13 Граф б) есть подграф графа а), а граф в) – часть графа а)
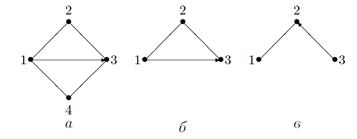
Рисунок 13 – Подграф и часть графа.
Основные операции с графами:
1. Добавление вершины. Ко множеству вершин добавляется новая вершина.
2. Добавление дуги. Дуга (a,b) добавляется за счет добавления двух вершин a и b ко множеству вершин и соответствующей дуги ко множеству дуг.
3. Удаление дуги заключается в удалении дуги (a,b) из множества дуг.
4. Удаление вершины заключается в удалении вершины из графа вместе со всеми инцидентными ребрами.
5. Отождествление вершин a и b заключается в удалении вершин a и b из графа и присоединением новой вершины 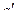 и дуг, соединяющих ее с теми вершинами, которые были смежны с a и b.
и дуг, соединяющих ее с теми вершинами, которые были смежны с a и b.
На рисунке 14 показаны следующие операции: 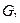 получен из G добавлением вершины 5, граф
получен из G добавлением вершины 5, граф 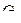 получен из
получен из 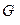 добавлением дуги (3,1), граф
добавлением дуги (3,1), граф 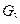 получен удалением дуги (3,2), граф
получен удалением дуги (3,2), граф 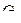 получен удалением вершины 2, граф
получен удалением вершины 2, граф 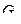 получен отождествлением вершин 1 и 4, граф
получен отождествлением вершин 1 и 4, граф 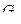 получен стягиванием дуги (2,3).
получен стягиванием дуги (2,3).
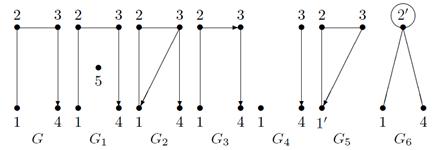
Рисунок 14 – Операции с графами.
6. Дополнением графа без петель называется граф, вершины которого совпадают с вершинами данного графа, а дуги соединяют вершины, не смежные в данном графе.
На рисунке 15 граф 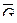 есть дополнение графа G на рисунке 14.
есть дополнение графа G на рисунке 14.
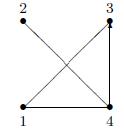
Рисунок 15 – Дополнение графа
Пусть даны графы 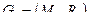 и
и 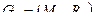 .
.
7. Объединением графов 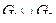 называется новый граф, в котором
называется новый граф, в котором 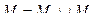 ,
, 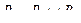 .
.
8. Пересечением графов 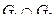 называется новый граф, в котором
называется новый граф, в котором 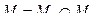 ,
, 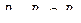 .
.
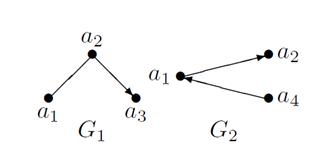
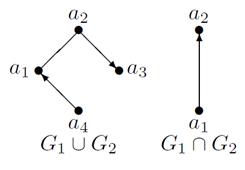
На рисунке 16 показаны объединения и пересечения графов 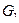 и
и 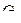 .
.
| 
|
Рисунок 16 – Объединение и пересечение графов
Маршруты и достижимость. Связность.
Маршрутом (путем) для графа G( V, X) называется последовательность v1 x1 v2 x2 v3… xkvk+1. Маршрут называется замкнутым, если его начальная и конечная точки совпадают. Число ребер (дуг) маршрута (пути) графа называется длиной маршрута (пути).
Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
Замкнутый маршрут (путь) называется циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.
Пример: Для графа, изображенного на рисунке 17, (1,2), (1,2,4,7), (3,4,5,6) являются простыми цепями, (1,2,4,7,8,4) – цепь, не являющаяся простой, (1,2,4,7,8,4,2) – маршрут, не являющийся цепью, (1,2,4,7,8,4,1) – цикл, не являющийся простым, (1,2,4,1) – простой цикл.
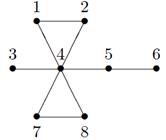
Рисунок 17 – Примеры маршрутов и цепей.
Вершина b называется достижимой из вершины a, если существует путь из a в b.
Матрица достижимости С – квадратная матрица, элементы которой удовлетворяют условию:
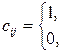
| если вершина 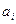 достижима из вершины достижима из вершины 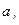 или i= j
в противном случае или i= j
в противном случае
|
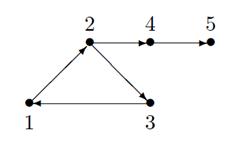
Пример. Для графа, изображенного на рисунке 18, матрица достижимости имеет вид:
| 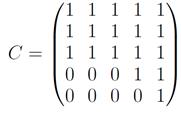
|
Рисунок 18 – Граф и его матрица достижимости
Неорграф называется связным, если любые его две несовпадающие вершины соединены маршрутом. Граф G называется связным, если соответствующий ему неорграф связный. Граф называется сильно связным, если для каждой пары различных вершин существуют маршруты из a в b и из b в a. Граф на рисунке 17 связанный, на рисунке 18 связный, но не сильно, на рисунке 19 не связный.
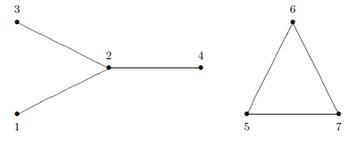
Рисунок 19 – Пример не связного графа
Всякий максимальный по включению связный (сильно) подграф данного графа называется его компонентой связности. На рисунке 19 граф имеет две компоненты связности: {1,2,3,4} и {5,6,7}. Нахождение компонентов связности происходит с помощью матрицы достижимости: 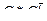 , где символом * обозначено поэлементное произведение матриц, и тогда сильная компонента связности состоит из вершин, для которых
, где символом * обозначено поэлементное произведение матриц, и тогда сильная компонента связности состоит из вершин, для которых 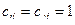 .
.
Пример. Для графа на рисунке 18
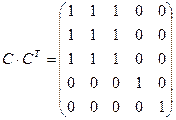 , значит его сильные компоненты связности {1,2,3}, {4}, {5}.
, значит его сильные компоненты связности {1,2,3}, {4}, {5}.
Расстояния в графах.
Пусть G – связный неорграф, a и b – две его несовпадающие вершины. Длина кратчайшего маршрута от a до b называется расстоянием между вершинами a и b.
Матрица расстояний – матрица Р, в которой 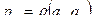 . Эта матрица симметрична.
. Эта матрица симметрична.
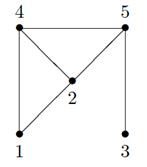
Пример. Для графа, изображенного на рисунке 19, матрица расстояний имеет вид:
| 
|
Рисунок 19 – Граф и его матрица расстояний.
Для фиксированной вершины а величина 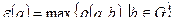 называется эксцентриситетом вершины a. Таким образом, эксцентриситет вершины равен расстоянию от нее до наиболее удаленной вершины. В матрице расстояний эксцентриситет вершины – наибольшее из чисел, стоящих в соответствующей строке.
называется эксцентриситетом вершины a. Таким образом, эксцентриситет вершины равен расстоянию от нее до наиболее удаленной вершины. В матрице расстояний эксцентриситет вершины – наибольшее из чисел, стоящих в соответствующей строке.
Минимальный из всех эксцентриситетов графа называется его радиусом r, Максимальный – диаметром d. Вершина а называется центральной, если ее эксцентриситет равен радиусу и периферийной, если ее эксцентриситет равен диаметру графа.
Пример: Для графа на рисунке 15 эксцентриситеты вершины равны:
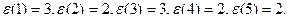
Диаметр графа  , радиус графа
, радиус графа 
Центральные вершины 2, 3,5; периферийные вершины 1, 3.
Степени вершин.
Степенью вершины 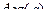 неорграфа G называется число ребер, инцидентных вершине а, т.е. число ребер, концом которых является вершина а, при этом петли считаются дважды. Для орграфа степень вершины определяется как степени соответствующего неорграфа.
неорграфа G называется число ребер, инцидентных вершине а, т.е. число ребер, концом которых является вершина а, при этом петли считаются дважды. Для орграфа степень вершины определяется как степени соответствующего неорграфа.
Пример. Для графа, изображенного на рисунке 20 степени вершин будут равны:
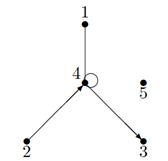
| 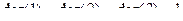
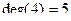
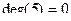 .
Вершины 1, 2, 3 называются изолированными, 5 – висячая. .
Вершины 1, 2, 3 называются изолированными, 5 – висячая.
|
Рисунок 20 – Стпени вершин графа
Имеет место следующие свойство: сумма степеней всех вершин графа является четным числом и равна удвоенному числу ребер.
Эйлеровы и гамильтоновы графы
Цикл, содержащий все ребра мультиграфа, называется эйлеровым, а граф, в котором имеет эйлеров цикл, называется эйлеровым графом.
Критерий наличия эйлерова цикла: чтобы неориентированный граф обладал эйлеровым циклом, необходимо и достаточно, чтобы он был связен, и все вершины графа имели четные степени.
Алгоритм построения эйлерова цикла состоит в следующем:
1. Выходим из произвольной вершины 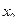 , каждое пройденное ребро зачеркиваем.
, каждое пройденное ребро зачеркиваем.
2. Никогда не идем по такому ребру, которое в рассматриваемый момент является перешейком (т.е. ребром, удаление которого разбивает граф на два компонента связности), а также не выбираем ребра, идущего в 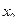 , пока есть другие возможности.
, пока есть другие возможности.
Орграф называется гамильтоновым, если в нем существует контур, включающий каждую его вершину по одному разу, сам контур называется гамильтоновым.
Пример: Пусть дан граф
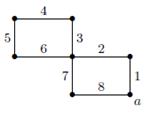 .
.
Он является эйлеровым. Найдем эйлеров цикл. Выбираем вершину а и ребро 1, потом ребро 2. Далее имеем выбор ребер 3,6 или 7. Ребро 7 является перешейком. Выбираем, например 3. Затем 4, 5, 6, 7,8. Получили эйлеров цикл.
Деревья.
Неориентированный граф с числом вершин n>1 называется деревом, если он связный и не содержит циклов.
Следующая теорема характеризует свойства деревьев, каждое из которых может служить определением дерева.
Теорема. Для графа G, имеющего n вершин (n>1), равносильны следующие свойства:
1. G связен и не содержит циклов;
2. G не содержит циклов и имеет (n-1) ребро;
3. G связен и имеет (n-1) ребро;
4. G не содержит циклов, но добавление ребра между любыми его вершинами при-
водит к образованию цикла;
5. G связен, и все его ребра являются перешейками;
6. Всякая пара вершин G соединена только одной цепью.
Ориентированное дерево называется прадеревом. Несвязный граф, компонентами связности которого являются деревья, называется лесом.
Дерево, полученное из связного графа G удалением нескольких ребер, называется остовным деревом, или просто остовом графа G. Ациклический граф, полученный из графа G удалением нескольких ребер, называется остовным подграфом графа G.
Взвешенным графом будем называть граф, на множестве ребер E которого задана функция 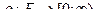 , называемая весовой.
, называемая весовой.
Число r называется весом ребра e.
Остов T связного взвешенного графа G назовем минимальным остовом, если для любого другого его остова 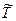 выполнено неравенство
выполнено неравенство 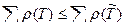 .
.
Рассмотрим задачу о нахождении минимального остова в связном взвешенном графе. Алгоритм Краскала:
1. Выбираем ребро с наименьшим весом.
2. На каждом шаге добавляем к остовному подграфу ребро минимального веса, не приводящее к образованию цикла.
3. Последним элементом последовательности является минимальный остов графа.
Примеры выполнения типовых заданий.
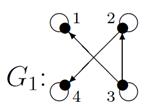
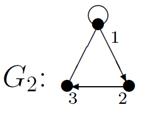
Пример №1. Для данных орграфов 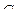 и
и 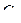 найти
найти 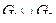 и
и 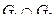 , для
, для 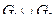 построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
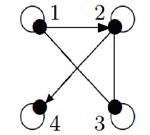
Решение.
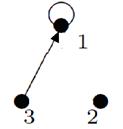
1. Объединение и пересечение графов показано на рисунке:
| 
|
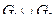
| 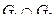
|
2. Матрица смежности для первого графа будет иметь вид:
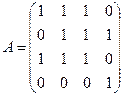
Матрица инцидентности для графа 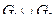 :
:
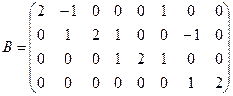
Матрица достижимости:
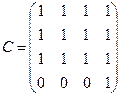 ,
,
Граф не является сильно связным. Компоненты связности:
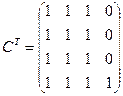 ,
, 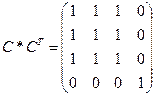 , значит сильные компоненты связности графа {1,2,3} и {4}.
, значит сильные компоненты связности графа {1,2,3} и {4}.
Пример №2. Для данного неорграфа найти матрицу расстояний. Определить степени вершин, эксцентриситеты вершин, радиус и диаметр графа, центральные и периферийные вершины. Является ли данный граф эйлеровым, если да, то найти эйлеров цикл.
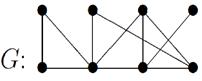
Решение.
Занумеруем вершины графа:
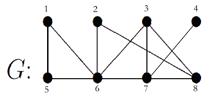
Матрица расстояний будет иметь вид:
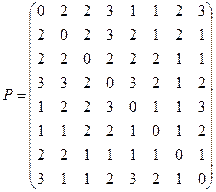
Тогда степени и эксцентриситеты вершин будут равны:
| вершина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| deg | 2 | 2 | 3 | 1 | 2 | 5 | 4 | 3 |
| ε | 3 | 3 | 2 | 3 | 3 | 2 | 2 | 3 |
Диаметр графа равен 3, радиус графа равен 2.
Центральные вершины 3, 6, 7, периферийные вершины 1, 2, 4, 5, 8.
Граф не является эйлеровым.
Пример № 3. Для данного графа найти минимальный остов.
V={a, b, c, d, e, f, g}, E={ab, ag, bc, cd, de, df, ef, fg}, r (ab) = 6, r (ag) = 9, r (bc) = 2, r (cd) = 4, r (de) = 5, r (df) = 3, r (ef) = 7, r (fg) = 8.
Решение.
Представим граф в графическом виде:
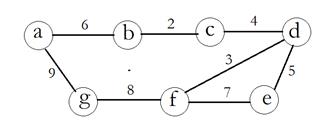
Выбираем ребро с минимальным весом (bc) = 2. Из оставшихся ребер добавляем последовательно с минимальными весами, следим за тем, чтобы не было цикла:
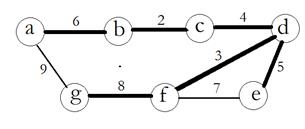
(fd) = 3, (cd) = 4, (de) = 5, (ab) = 6. Ребро (ef) не может быть добавлено, так образуется цикл: fed. Добавляем (fg) = 8. Ребро (ag) не может быть добавлено.
Полученный остов выделе на рисунке.
Задания для совместного решения.
1. Для данных орграфов  и
и  найти
найти 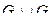 и
и 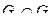 , для
, для 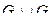 построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
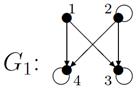 ,
, 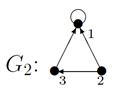
2. Для данного неорграфа найти матрицу смежности, матрицу инцидентности, матрицу расстояний. Определить степени вершин, эксцентриситеты вершин, радиус и диаметр графа, центральные и периферийные вершины. Является ли данный граф эйлеровым, если да, то найти эйлеров цикл.
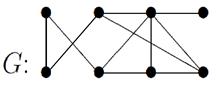
3. Для данного графа найти минимальный остов.
V={a, b, c, d, e, f, g, h}, E={ac, af, ah, bc, bh, ce, ch, de, df, ef, eh,fg, gh}, r (ac) = 2, r (af) = 9, r (ah) = 2, r (bc) = 3, r (bh) = 4, r (ce)= 7, r (ch) = 3, r (de) = 2, r (df) = 8, r (ef) = 5, r (eh) = 9, r (fg) = 1, r (gh) = 2.
Индивидуальные контрольные задания.
1. Для данных орграфов 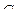 и
и 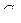 найти
найти 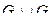 и
и 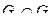 , для
, для 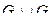 построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
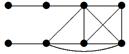
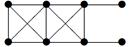
2. Для данного неорграфа найти матрицу смежности, матрицу инцидентности, матрицу расстояний. Определить степени вершин, эксцентриситеты вершин, радиус и диаметр графа, центральные и периферийные вершины. Является ли данный граф эйлеровым, если да, то найти эйлеров цикл.
3. Для данного графа найти минимальный остов.
| 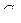
| Задание 2 | Задание 3 | |
| 1 | 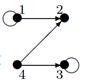
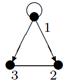
| 
| 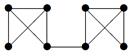
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 5, r ( ag ) = 7, r ( ah ) = 2, r ( bc ) = 3, r ( bh ) = 3, r ( cd ) =1, r ( ch ) = 9, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 11, r ( eh ) = 2, r ( fg ) = 5, r ( fh ) = 8. |
| 2 | 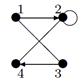
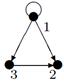
| 
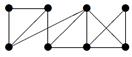
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 5, r ( ag ) = 7, r ( ah ) = 2, ( bc ) = 12, r ( bh ) = 3, r ( cd ) =10, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 11, r ( eh ) = 2, r ( fg ) = 5, r ( fh ) = 7. |
| 3 | 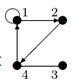
| 
| 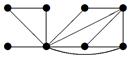
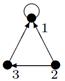
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 2, r ( ag ) = 7, r ( ah ) = 2, r ( bc ) = 12, r ( bh ) = 5, r ( cd ) =10, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 5, r ( fh ) = 6. |
| 4 | 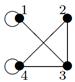
| 
| 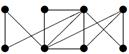
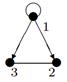
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 2, ( ag ) = 7, r ( ah ) = 2, r ( bc ) = 2, r ( bh ) = 5, r ( cd ) =9, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 5, r ( fh ) = 3. |
| 5 | 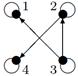
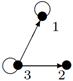
| 
| 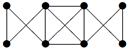
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 2, r ( ag ) = 1, r ( ah ) = 9, r ( bc ) = 2, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 15, r ( fh ) = 3. |
| 6 | 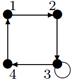
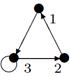
| 
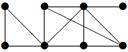
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 2, r ( ag ) = 1, r ( ah ) = 9, r ( bc ) = 2, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 15, r ( gh ) = 3. |
| 7 | 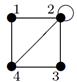
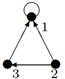
| 
| 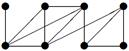
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 1, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 9, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 15, r ( gh ) = 3. |
| 8 | 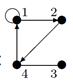
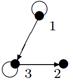
| 
| 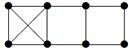
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 6, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 9, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 2, r ( gh ) = 9. |
| 9 | 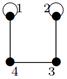
| 
| 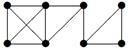
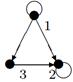
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =4, r ( ch ) = 6 r ( de ) = 9, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 2, r ( gh ) = 9. |
| 10 | 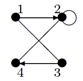
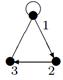
| 
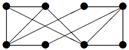
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 4, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 2, r ( fg ) = 2, r ( gh ) = 9. |
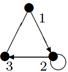
| 11 | 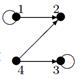
| 
| 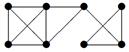
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =4, r ( ch ) = 6, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 2, r ( fg ) = 7, r ( gh ) = 9. |
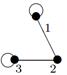
| 12 | 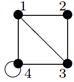
| 
| 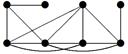
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 5, r ( bc ) = 3, r ( bh ) = 8, r ( cd ) =4, r ( ch ) = 6, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 7, r ( fg ) = 2, r ( gh ) = 9. |
| 13 | 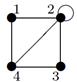
| 
| 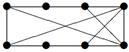
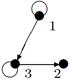
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , af , ah , bc , bh , ce , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 2, r ( af ) = 3, r ( ah ) = 5, ( bc ) = 3, r ( bh ) = 8, r ( ce )= 4, r ( ch ) = 6, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 10, r ( fg ) =7, r ( gh ) = 2 |
| 14 | 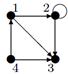
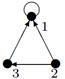
| 
| 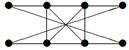
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , af , ah , bc , bh , ce , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 2, r ( af ) = 3, r ( ah ) = 5, ( bc ) = 3, r ( bh ) = 8, r ( ce )= 7, r ( ch ) = 6, r ( de ) = 1, r ( df ) = 3, r ( ef ) = 5, r ( eh ) = 10, r ( fg ) =7, r ( gh ) = 2 |
| 15 | 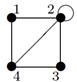
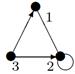
| 
| 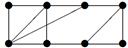
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , af , ah , bc , bh , ce , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 6, r ( af ) = 3, r ( ah ) = 5, ( bc ) = 3, r ( bh ) = 8, r ( ce )= 7, r ( ch ) = 11, r ( de ) = 1, r ( df ) = 3, r ( ef ) = 2, r ( eh ) = 10, r ( fg ) =7, r ( gh ) = 2 |
| 16 | 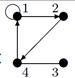
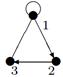
| 
| 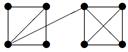
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 3, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 4, r ( bf ) = 1, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 1, r ( eg ) = 1, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
| 17 | 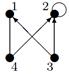
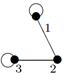
| 
| 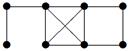
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 4, r ( bf ) = 5, r ( cd ) =3, r ( de ) = 1, r ( ef ) = 5, r ( eg ) = 2, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
| 18 | 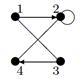
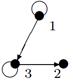
| 
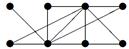
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 4, r ( bf ) = 5, r ( cd ) =3, r ( de ) = 1, r ( ef ) = 5, r ( eg ) = 2, r ( fg ) = 2, r ( fh ) = 1, r ( gh ) = 3. |
| 19 | 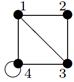
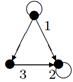
| 
| 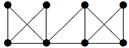
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 1, r ( ad ) = 4, r ( bd ) = 2, r ( bf ) = 5, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 1, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
| 20 | 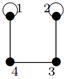
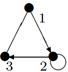
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 1, r ( ad ) = 4, r ( bd ) = 2, r ( bf ) = 1, r ( cd ) =6, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
| 21 | 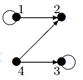
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 1, r ( ad ) = 4, r ( bd ) = 2, r ( bf ) = 1, r ( cd ) =2, r ( de ) = 6, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 7, r ( gh ) = 2. |
| 22 | 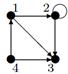
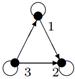
| 
| 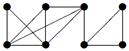
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 1, r ( cd ) =6, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 1, r ( gh ) = 3. |
| 23 | 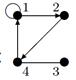
| 
| 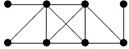
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 1, r ( gh ) = 3. |
| 24 | 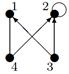
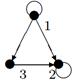
| 
| 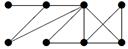
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 3, r ( gh ) = 1. |
| 25 | 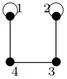
| 
| 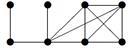
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 1, r ( eg ) = 2, r ( fg ) = 1, r ( fh ) = 5, r ( gh ) = 3. |
| 26 | 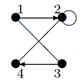
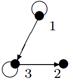
| 
| 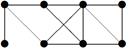
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 1, r ( ef ) = 2, r ( eg ) = 1, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 1. |
| 27 | 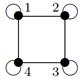
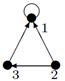
| 
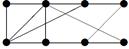
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 1, r ( ef ) = 2, r ( eg ) = 5, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 7. |
| 28 | 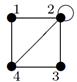
| 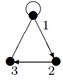
| 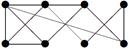
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =6, r ( de ) = 4, r ( ef ) = 1, r ( eg ) = 5, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 7. |
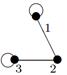
| 29 | 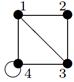
| 
| 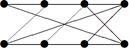
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 5, r ( bd ) = 3, r ( bf ) = 4, r ( cd ) =6, r ( de ) = 4, r ( ef ) = 1, r ( eg ) = 5, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 1. |
| 30 | 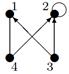
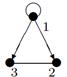
| 
| 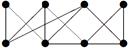
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 5, r ( bd ) = 3, r ( bf ) = 1, r ( cd ) =2, r ( de ) = 4, r ( ef ) = 1, r ( eg ) = 3, r ( fg ) = 2, r ( fh ) = 3, r ( gh ) = 1. |
Раздел 5. Элементы теории алгоритмов
Тема 5.1.Элементы теории алгоритмов
Практическая работа №16. Работа машины Тьюринга
Дата: 2018-12-28, просмотров: 520.