Теория отображений. Алгебра подстановок.
В математическом анализе понятие функции вводится следующим образом:
Пусть Х – некоторое множество на числовой прямой. Говорят, что на этом множестве определена функция f , если каждому числу х 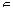 Х поставлено в соответствие определенное число
Х поставлено в соответствие определенное число 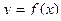 . При этом Х называется областью определения, Y есть совокупность всех значений, принимаемых этой функцией, и называется областью значений. Если же вместо числовых рассматривать множества какой либо другой природы, то придем к самому общему понятию функции.
. При этом Х называется областью определения, Y есть совокупность всех значений, принимаемых этой функцией, и называется областью значений. Если же вместо числовых рассматривать множества какой либо другой природы, то придем к самому общему понятию функции.
Пусть А и В – два произвольных множества. Говорят, что на множестве А определена функция f, принимающая значения из В, если каждому элементу х 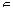 А поставлено в соответствие один и только один элемент из В.
А поставлено в соответствие один и только один элемент из В.
Для множеств произвольной (не числовой) природы вместо термина “функция” пользуются термином “отображение”, говоря об отображении одного множества в другое. Для обозначения функции (отображения) из А в В пользуются записью:
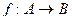
Если а – элемент из А, то соответствующий ему элемент 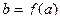 из В называется его образом (при отображении f). Совокупность всех тех элементов а из А, образом которых является данный элемент b
из В называется его образом (при отображении f). Совокупность всех тех элементов а из А, образом которых является данный элемент b 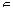 В, называется прообразом (полным образом) элемента b и обозначается
В, называется прообразом (полным образом) элемента b и обозначается 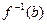 .
.
Пусть Х некоторое множество из А. Совокупность {f(a) | a 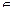 Х} всех элементов вида f(a), где а
Х} всех элементов вида f(a), где а 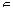 Х, называется образом Х и обозначается f(Х). В свою очередь для каждого множества Y из B определяется его полный образ
Х, называется образом Х и обозначается f(Х). В свою очередь для каждого множества Y из B определяется его полный образ 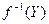 , а именно:
, а именно: 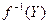 есть совокупность всех тех элементов из A, образы которых принадлежат
есть совокупность всех тех элементов из A, образы которых принадлежат 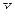 .
.
Определено, что f есть отображение множества A на множество B, если f(A)=B. Такое отображение называют также сюръекцией. В общем случае, т.е. когда f(A) 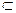 B, говорят, что f есть отображение A в B. Если f(A) состоит из единственного элемента, то f называется функцией-константой.
B, говорят, что f есть отображение A в B. Если f(A) состоит из единственного элемента, то f называется функцией-константой.
Отображение f называется сюръективным отображением, если все элементы во множестве Y являются образами какого-либо x.
Если для любых двух различных элементов 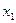 и
и 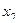 из А их образы
из А их образы 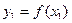 и
и 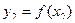 также различны, то f называется инъекцией. Отображение f называется инъективным отображением, если
также различны, то f называется инъекцией. Отображение f называется инъективным отображением, если 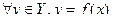 является образом единственного x.
является образом единственного x.
Отображение 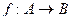 , которое одновременно является и сюръекцией и инъекцией, называется биекцией или взаимно-однозначным соответствием между А и В.
, которое одновременно является и сюръекцией и инъекцией, называется биекцией или взаимно-однозначным соответствием между А и В.
На рисунке 10 показана графическая интерпретация видов отображений.
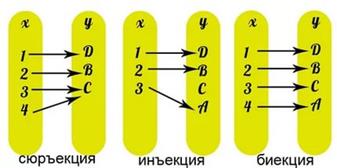
Рисунок 10 – Различные виды отображений
Пример 1. Различные виды отображений

| Инъективное, не сюръективное. (элемент 5 не имеет прообраза) |
 
| Не отображение (элемент b не имеет образа, во втором примере элементу с соответствует два образа) |

| Отображение. Не инъективное, сюръективное. (элемент 1 имеет два прообраза) |

| Отображение. Инъективное, сюръективное ⇒ биективное. |
Взаимно-однозначное отображение  называют подстановкой на Х.
называют подстановкой на Х.
Обозначают, как правило, π или маленькими буквами латинского алфавита.
Существует несколько способов задания перестановки. Явное задание перестановки:
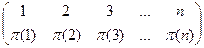
В записи выше первая строка всегда одинакова. Элементы второй строки являются перестановкой элементов первой строки.
Определяются операции с подстановками:
1. Произведение (композиция).
Пусть 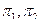 подстановки одного порядка. Тогда произведением их назовем новую подстановку
подстановки одного порядка. Тогда произведением их назовем новую подстановку 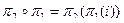 ,
, 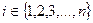
Пример.
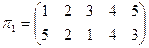 ,
, 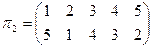 .
.
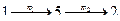 ,
, 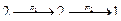 ,
, 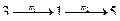 и т.д.
и т.д.
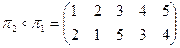 .
.
 .
.
Из примера следует, что операция некоммутативна.
2. Тождественная подстановка 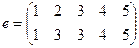 .
.
3. Обратная подстановка 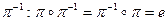 .
.
Обратную подстановку можно получить, если поменять местами строки исходной таблицы.
Пример.
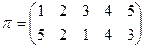 ,
,
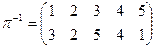 .
.
4. Два элемента образуют инверсию, если 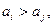 при i< j.
при i< j.
Подстановка называется четной (нечетной), если сумма инверсий, образуемых элементами подстановки, четная (нечетная).
Решение простейших уравнений в алгебре подстановок.
| Уравнение | Решение |
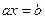
| 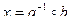
|
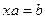
| 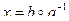
|
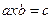
| 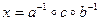
|
Примеры выполнения типовых заданий.
Пример №1. Определить число инверсий и четность подстановки.
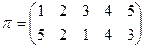 .
.
Решение.
С элементом 5 инверсию образуют все идущие за ним элементы 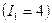 , с 2 инверсию образует только 1
, с 2 инверсию образует только 1 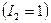 , с единицей нет инверсий, с 4 инверсию образует 3.
, с единицей нет инверсий, с 4 инверсию образует 3.
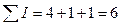 , четная подстановка.
, четная подстановка.
Пример №2. С данными подстановками выполните следующие операции:
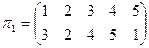 ,
, 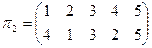 .
.
| а) | 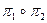
| б) | 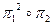
| в) | 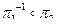
|
Решение.
а) 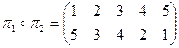 .
.
б) 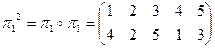 .
.
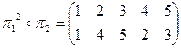 .
.
в) 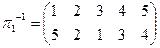 .
.
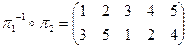 .
.
Пример №3. Даны подстановки:
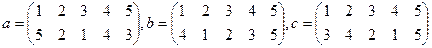 .
.
Решить уравнения: 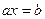 ,
, 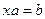 ,
, 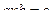 .
.
1. 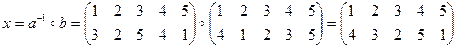 .
.
 2.
2. 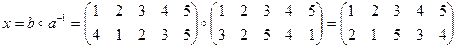
3.
Задания для совместного решения.
1. Определить число инверсий и четность подстановки:
а) 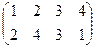 б)
б) 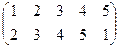 в)
в) 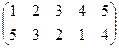
2. С данными подстановками выполните следующие операции:
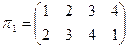
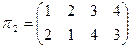
а) 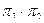 б)
б) 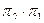 в)
в) 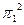
г) 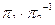 д)
д) 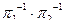 е)
е) 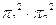
3. Решить уравнения:
а ) a × x = b б ) x × a = b в ) a × x × b = c
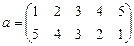
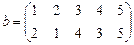
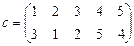 .
.
Ответы:
1. а) 3, нечетная б) 4, четная, в) 6, четная.
2. а) 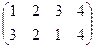 , б)
, б) 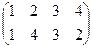 , в)
, в) 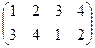 , г)
, г) 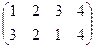
д) 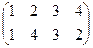 , е)
, е) 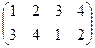 .
.
3. а) 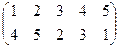 , б)
, б) 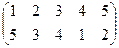 , в)
, в) 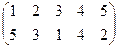 .
.
Индивидуальные контрольные задания.
1. Определить число инверсий и четность подстановок a, b, c.
2. С данными подстановками выполните следующие операции: 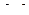 ,
, 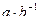 ,
, 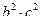 .
.
3. Решить уравнения:
а) a × x = b б) x × a = b в) a × x × b = c
| a | b | c | |
| 1 | 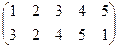
| 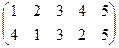
| 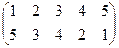
|
| 2 | 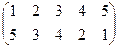
| 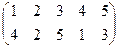
| 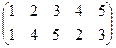
|
| 3 | 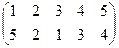
| 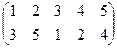
| 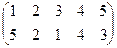
|
| 4 | 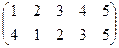
| 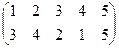
| 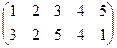
|
| 5 | 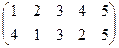
| 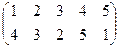
| 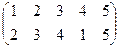
|
| 6 | 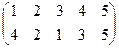
| 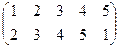
| 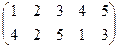
|
| 7 | 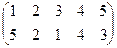
| 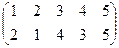
| 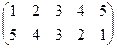
|
| 8 | 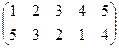
| 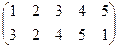
| 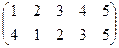
|
| 9 | 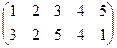
| 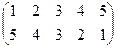
| 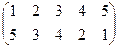
|
| 10 | 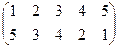
| 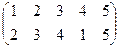
| 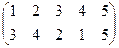
|
| 11 | 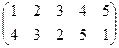
| 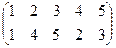
| 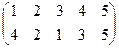
|
| 12 | 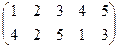
| 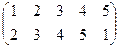
| 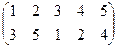
|
| 13 | 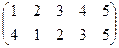
| 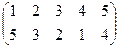
| 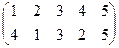
|
| 14 | 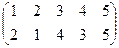
| 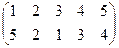
| 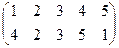
|
| 15 | 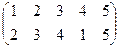
| 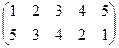
| 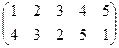
|
| 16 | 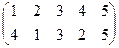
| 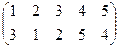
| 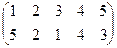
|
| 17 | 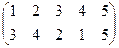
| 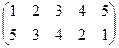
| 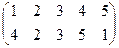
|
| 18 | 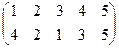
| 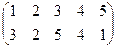
| 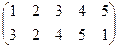
|
| 19 | 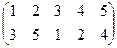
| 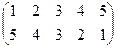
| 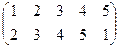
|
| 20 | 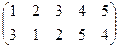
| 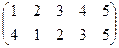
| 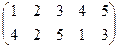
|
| 21 | 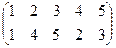
| 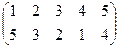
| 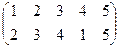
|
| 22 | 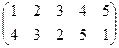
| 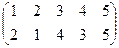
| 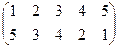
|
| 23 | 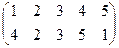
| 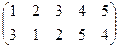
| 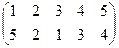
|
| 24 | 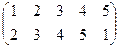
| 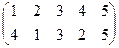
| 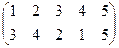
|
| 25 | 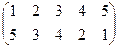
| 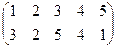
| 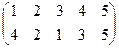
|
| 26 | 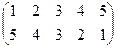
| 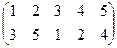
| 
|
| 27 | 
| 
| 
|
| 28 | 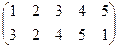
| 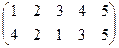
| 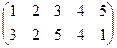
|
| 29 | 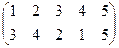
| 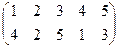
| 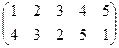
|
| 30 | 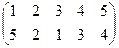
| 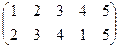
| 
|
Раздел 3. Логика предикатов
Тема 3.1. Предикаты
Практическая работа №13. Нахождение области определения и истинности предиката. Построение отрицаний к предикатам, содержащим кванторные операции.
Дата: 2018-12-28, просмотров: 454.