Отношения. Бинарные отношения и их свойства.
Пусть заданы множества M и L.
Бинарным отношением называется подмножество r ⊆ M × L.
Если r отношение, то пишут: x ∈ M, y ∈ L, 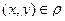 , либо (x, y)∈ r, либо xry и говорят: x находится в отношении r к y, либо выполняется соотношение xry.
, либо (x, y)∈ r, либо xry и говорят: x находится в отношении r к y, либо выполняется соотношение xry.
Пример.
1. S — множество групп, T — множество преподавателей.
r ⊆ S × T, xry, x ∈ S, y ∈ T; xry – группа x слушает лекции преподавателя y.
2. Отношение “быть старше”: r ⊆ M × M, xry – x старше y.
3. Отношение “быть севернее”: r⊆ M × M, xry – город x находится севернее города y.
4. Отношение “быть знакомым с”: xry – x знаком с y.
5. Отношение “<“: (2;5)∈r, (5;2) 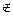 r.
r.
Способы задания бинарного отношения.
1. Бинарное отношение можно задавать перечислением всех упорядоченных пар – элементов отношения.
2. Задание отношения матрицей. Пусть |M| = n и элементы M = 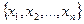 пронуме- рованы целыми числами от 1 до n. Квадратная матрица размерностью n × n задает бинарное отношение, если i-я строка матрицы соответствует i-му элементу M, j-й столбец – j-му элементу M,
пронуме- рованы целыми числами от 1 до n. Квадратная матрица размерностью n × n задает бинарное отношение, если i-я строка матрицы соответствует i-му элементу M, j-й столбец – j-му элементу M,
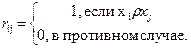
Матрица отношения содержит всю информацию о том, какие пары элементов из M принадлежат отношению r.
3. Представление отношения графом. Граф G = (M, r) задан, если задано множество M и бинарное отношение r на нем. Элементы множества M называются вершинами графа, а пары ( x, y) ∈r – дугами (пары вида ( x, x) называются петлями). Для небольших размерностей удобно иллюстрировать отношения с помощью диаграммы. Элементы множества M (вершины графа) изображаются в виде точек на плоскости; если пара ( x, y)∈ r, то x, y соединяют стрелкой, идущей из x в y. Эту диаграмму также называют графом.
Пример. Пусть 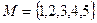 и бинарное отношение
и бинарное отношение 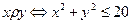 .
.
Перечисление пар, состоящих в отношении:
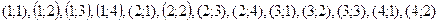
Матрица отношения:
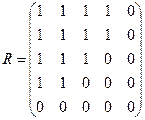 .
.
Граф отношения:
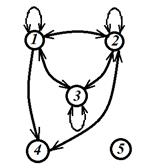
Виды бинарных отношений.
Пусть заданы конечное множество M мощности |M| = n и отношения A, B, C ⊆ M×M.
Отношение A называется рефлексивным, ∀x ∈ M [xAx].
К рефлексивным относятся отношения типа “ 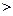 “
“ 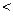 ”, “быть похожим на”, “быть равным”. Матрица, представляющая рефлексивное отношение, имеет все единицы на главной диагонали. В графе, представляющем рефлексивное отношение, при каждой вершине имеется петля.
”, “быть похожим на”, “быть равным”. Матрица, представляющая рефлексивное отношение, имеет все единицы на главной диагонали. В графе, представляющем рефлексивное отношение, при каждой вершине имеется петля.
Отношение A называется антирефлексивным, если ∀x, y ∈ M [xAy ⇒ x 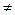 y].
y].
К антирефлексивным относятся отношения типа “<“ , “>“, “быть моложе“, “быть предком“, “быть потомком“ и т.д. Главная диагональ матрицы, представляющей антирефлексивное отношение, содержит только нули, а в соответствующем графе отсутствуют петли.
Отношение A называется симметричным, если ∀x, y ∈ M [xAy ⇒ yAx]. Симметричные отношения – это отношения типа “быть одинаковым с”, “быть похожим на”, “быть родственником с” и т.д. Элементы матрицы, представляющей симметричное отношение, расположенные симметрично относительно главной диагонали, равны между собой. В соответствующем графе, если существует дуга, идущая из вершины x в вер- шину y, то существует и дуга, идущая из y в x. Часто граф симметричного отношения изображают как неориентированный – пара симметричных дуг заменяется звеном.
Отношение A называется асимметричным, если из двух отношений xAy или yAx по крайней мере одно не выполняется. Примерами асимметричных отношений могут служить “<“ , “>“ и т.д. В матрице, представляющей асимметричное отношение, 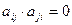 т.е. если элемент
т.е. если элемент 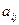 = 1, то
= 1, то 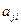 = 0, но возможно
= 0, но возможно 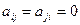 . В соответствующем графе любую пару вершин соединяет не более одной дуги, петли отсутствуют.
. В соответствующем графе любую пару вершин соединяет не более одной дуги, петли отсутствуют.
Отношение A называется антисимметричным, если 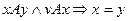 . Для элементов матрицы, представляющей антисимметричное отношение,
. Для элементов матрицы, представляющей антисимметричное отношение, 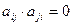 , если i
, если i 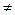 j. В соответствующем графе любую пару вершин соединяет не более одной дуги, но могут быть и петли. В матрице антисимметричного отношения
j. В соответствующем графе любую пару вершин соединяет не более одной дуги, но могут быть и петли. В матрице антисимметричного отношения 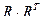 все элементы вне главной диагонали нулевые.
все элементы вне главной диагонали нулевые.
Отношение A называется транзитивным, ∀x, y, z ∈ M [xAz ∧ zAy ⇒ xAy].
Свойства отношений 67 Из определения по индукции следует такое свойство: если выполнены соотношения xAz1, z1Az2, . . . , zn−1Ay, выполнится и xAy. Для матрицы транзитивного отношения выполняется условие: 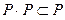 . Умножение матриц выполняется обычным способом, но при этом, умножение элементов соответствует логическому «и» (0∙0=1∙0=0∙1=0, 1∙1=1), а сложение элементов – логическому «или» (0+0=0, 1+0=0+1=1+1=1). На графе, представляющем транзитивное отношение, любая ориентированная цепочка из x в y замыкается дугой (x, y). Транзитивность плохо распознается на матрицах, но хорошо распознается на графах: бинарное отношение транзитивно тогда и только тогда, когда любая двухзвенная направленная ломаная в соответствующем орграфе замыкается стрелкой из начала этой ломаной в ее конец. Примеры транзитивного отношения: “быть предком“, отношения “< “, “>“ на числовой оси и т.д.
. Умножение матриц выполняется обычным способом, но при этом, умножение элементов соответствует логическому «и» (0∙0=1∙0=0∙1=0, 1∙1=1), а сложение элементов – логическому «или» (0+0=0, 1+0=0+1=1+1=1). На графе, представляющем транзитивное отношение, любая ориентированная цепочка из x в y замыкается дугой (x, y). Транзитивность плохо распознается на матрицах, но хорошо распознается на графах: бинарное отношение транзитивно тогда и только тогда, когда любая двухзвенная направленная ломаная в соответствующем орграфе замыкается стрелкой из начала этой ломаной в ее конец. Примеры транзитивного отношения: “быть предком“, отношения “< “, “>“ на числовой оси и т.д.
Отношение A называется антитранзитивным, если выполнена цепочка соотношений x = z0Az1 ∧ z1Az2 ∧ · · · ∧ zk−1Azk = y, то xAy невозможно, и наоборот, если выполнено соотношение xAy, то цепочка x = z0Az1 ∧ z1Az2 ∧ · · · ∧ zn−1Azk = y невозможна.
Отношение A на множестве M называется отношением эквивалентности (эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Пример.
1. Отношение равенства на числовой прямой: рефлексивно, симметрично, транзитивно, значит эквивалентно.
2. Отношение параллельности прямых: рефлексивно, симметрично, транзитивно, значит эквивалентно.
3. Отношение подобия треугольников: рефлексивно, симметрично, транзитивно, значит эквивалентно.
4. Отношение «жить на одном этаже»: рефлексивно, симметрично, транзитивно, значит эквивалентно.
5. Отношение «располагаться севернее»: антирефлексивно, асимметрично, транзитивно.
Примеры выполнения типовых заданий.
Пример №1. На множестве М {1, 2, 3, 4 } задано бинарное отношение 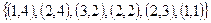 . Составить матрицу отношения, граф отношения. Определить вид отношения.
. Составить матрицу отношения, граф отношения. Определить вид отношения.
Решение.
Матрица отношения будет иметь вид:
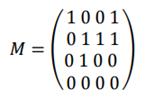 .
.
Граф отношения будет иметь вид:
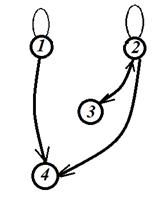
Отношение не относится ни к одному из указанных выше видов.
Пример №2. Пусть A={1, 2, 3, 4}, на множестве A заданы два отношения:
R={(x, y) | 2x 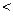 y} и P={(x, y) | x+3y делится на 2}. Какими свойствами обладают отношения R, P?
y} и P={(x, y) | x+3y делится на 2}. Какими свойствами обладают отношения R, P?
Решение.
Запишем отношения в виде множеств:
R={(1,2); (1,3); (1,4); (2,4)}. В частности, 1R2, поскольку 2·1 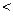 2.
2.
P={(1,1); (1,3); (2,2); (2,4); (3,1); (3,3); (4,2); (4,4)}. В частности, 1P3, поскольку 1+3·3 делится на 2.
Запишем матрицы отношений:
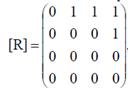 ,
, 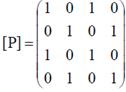 .
.
Отношение P является рефлексивным, а отношение R не является рефлексивным (в матрицах отношений на главной диагонали имеются нули).
Отношение R является антирефлексивным, а отношения P не является антирефлексивным (в матрицах отношений на главной диагонали имеются единицы).
Найдем транспонированные матрицы отношений.
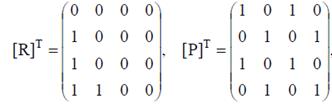 .
.
Из сравнения матриц отношений с транспонированными матрицами этих отношений, находим, что отношение P является симметричным, а отношения R не является симметричным. Отношение R является антисимметричными (у матрицы [R] и [R]T нет совпадающих единиц вне главной диагонали), а отношение P не является антисимметричным (например, p13=p31=1).
Для определения транзитивности отношений найдем произведения каждой матрицы на саму себя.

Задания для совместного решения.
На множестве М {1, 2, 3, 4} задано бинарное отношение
1. 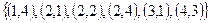 .
.
2. 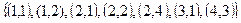
3. 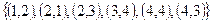
4. 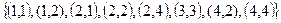
Составить матрицу отношения, граф отношения. Определить вид отношения.
Индивидуальные контрольные задания.
На множестве М {1, 2, 3, 4} задано бинарное отношение наборами пар. Составить матрицу отношения, граф отношения. Определить вид отношения.
| 1 | R={(1;1); (1;2); (1;3); (1;4); (2;2); (2;3); (2;4); (3;3); (3;4); (4;4)}. | 16 | R={(1;1); (1;2); (1;4); (2;2); (2;4); (3;3); (3;4); (4;4)}. |
| 2 | R={(1;1); (2;1); (1;2); (2;4); (4;2); (1;4); (4;1)}. | 17 | R={(1;1); (1;2); (2;4); (4;2); (1;4); (4;1); (4;3)}. |
| 3 | R={(2;1); (1;2); (2;3); (3;2); (1;3); (3;1)}. | 18 | R={(2;1); (1;2); (2;3); (3;2); (1;3); (3;1); (4;3)}. |
| 4 | R={(1;2); (2;3); (3;4); (4;1)}. | 19 | R={(1;2); (2;3); (3;4); (4;1);(4;3)}. |
| 5 | R={(1;1); (2;1); (2;2); (3;1); (3;2); (3;3); (4;1); (4;2); (4;3)}. | 20 | R={(1;1); (2;1); (2;2); (3;1); (3;2); (3;3); (4;1); (4;3)}. |
| 6 | R={(2;1); (2;2); (2;4); (3;4); (4;1); (4;2); (4;3); (4;4)} | 21 | R={(2;1); (2;2); (2;4); (3;3); (4;1); (4;2); (4;3); (4;4)} |
| 7 | R={(1;3); (2;4); (3;1); (3;4); (4;2); (4;3)}. | 22 | R={(1;3); (2;4); (3;1); (3;4); (4;2); (4;3);(4;4)}. |
| 8 | R={(1;1); (2;1); (2;3); (2;4); (3;2); (3;3); (3;4); (4;3); (4;4)}. | 23 | R={(1;1); (2;1); (2;2); (2;4); (3;2); (3;3); (3;4); (4;3); (4;4)}. |
| 9 | R={(1;1); (2;1); (1;2); (2;4); (2;2); (4;2); (1;4); (3;3); (4;1); (4;4)}. | 24 | R={(1;1); (2;1); (1;2); (2;4); (2;2); (4;2); (1;4); (4;1); (4;4)}. |
| 10 | R={(1;3); (2;1); (2;2); (2;4); (3;2); (3;4); (4;4)}. | 25 | R={(1;3); (2;1); (2;2); (2;4); (3;2); (3;4);(4;3); (4;4)}. |
| 11 | R={(1;3); (1;4); (2;2); (2;3); (2;4); (4;2); (3;4); (4;4)}. | 26 | R={(1;1); (1;4); (2;2); (2;3); (2;4); (4;2); (3;3); (4;4)}. |
| 12 | R={(1;1); (1;2); (2;4); (2;2); (1;4); (3;3); (4;4)}. | 27 | R={(1;1); (2;2); (2;4); (2;2); (1;4); (3;3); (4;4)}. |
| 13 | R={(1;1); (2;1); (2;2); (4;2); (4;1); (4;4)}. | 28 | R={(1;1); (2;1); (2;2); (4;2); (4;1); (4;4);(4;3)}. |
| 14 | R={(1;1); (2;1); (1;2); (2;4); (2;2); (4;2); (1;4); (4;1); (4;4)}. | 29 | R={(1;1); (2;1); (1;2); (2;4); (2;3); (3;2); (1;4); (4;1); (4;4)}. |
| 15 | R={(1;2); (1;3); (1;4); (2;3); (2;4); (3;4)}. | 30 | R={(1;2); (1;3); (1;4); (3;3); (3;4); (4;4)}. |
Практическая работа №12. Теория отображений и алгебра подстановок.
Дата: 2018-12-28, просмотров: 439.