Основные классы функций. Полнота множества. Теорема Поста.
Основные классы функций (классы Поста).
- Класс функций сохраняющих 0.
Говорят, что булева функция сохраняет 0, если f (0, 0,...,0) = 0 .
Множество всех булевых функций, сохраняющих 0, обозначается 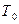 .
.
Примерами булевых функций, сохраняющих 0, являются конъюнкция и дизъюнкция, а импликация и эквиваленция не сохраняют 0.
- Класс функций сохраняющих 1.
Говорят, что булева функция сохраняет 1, если f (1,1,...,1)=1.
Множество всех булевых функций, сохраняющих 1, обозначается 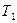 .
.
Примерами булевых функций, сохраняющих 1, являются конъюнкция, дизъюнкция, импликация, эквиваленция.
- Класс самодвойственных функций.
Обозначается S.
Булева функция называется самодвойственной, если на противоположных наборах ее значения противоположны, то есть 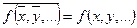 .
.
Проверить функцию на самодвойственность можно, совершив инверсию над всеми переменными и над самой функцией. Если при этом выражение получится таким же, то функция самодвойственна. Другой способ проверки – с помощью таблицы истинности. Если перевернуть столбец значений функции на 180о и совершить инверсию над полученным столбиком, то получив аналогичный исходному столбец, можно сделать вывод, что функция является самодвойственной.
- Класс линейных функций.
Обозначается L.
Булева функция называется линейной, если ее многочлен Жегалкина не содержит конъюнкций переменных.
- Класс монотонных функций.
Обозначается М.
Если для любого 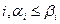 то говорят, что вектор
то говорят, что вектор 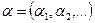 предшествует вектору
предшествует вектору 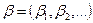 и пишут
и пишут 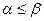
 Например:
Например: 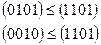
Говорят, что булева функция f монотонна, если для любых наборов α и β значений переменных, таких что, 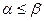 выполняется неравенство
выполняется неравенство 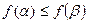 .
.
Примерами монотонных функций являются конъюнкция и дизъюнкция. Импликация, очевидно, немонотонна, поскольку ее значение на векторе (1,0) меньше значения на векторе (0,0), предшествующем вектору (1,0). Функция f = (10100110) также немонотонна: вектор (1,0,0) предшествует вектору (1,0,1), но f (1,0,0) = 1 > 0 = f (1,0,1).
Классы 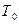 ,
, 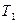 , S , L, M называют классами Поста.
, S , L, M называют классами Поста.
Утверждение. Классы Поста неполны и попарно различны.
Множество булевых функций 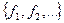 называется полной системой, если любая булева функция может быть реализована формулой над этим множеством.
называется полной системой, если любая булева функция может быть реализована формулой над этим множеством.
Теорема Поста. Система булевых функций полна тогда и только тогда, когда для каждого из классов 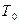 ,
, 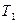 , S , L, M в этой системе найдется хотя бы одна функция, которая этому классу не принадлежит. Т.е. система содержит хотя бы одну функцию, не принадлежащую классам
, S , L, M в этой системе найдется хотя бы одна функция, которая этому классу не принадлежит. Т.е. система содержит хотя бы одну функцию, не принадлежащую классам 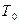 ,
, 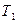 , S , L, M.
, S , L, M.
Чтобы проверить выполнение условий теоремы Поста, составляют таблицу Поста, столбцы которой соответствуют классам 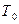 ,
, 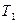 , S , L, M, строки – функциям, а в клетках проставляется «+» или «–» в зависимости от того, принадлежит ли функция соответствующему классу или не принадлежит. Если каждый столбец таблицы будет содержать хотя бы один «–», то система является полной.
, S , L, M, строки – функциям, а в клетках проставляется «+» или «–» в зависимости от того, принадлежит ли функция соответствующему классу или не принадлежит. Если каждый столбец таблицы будет содержать хотя бы один «–», то система является полной.
Примеры выполнения типовых заданий.
Пример №1. Выяснить, каким классам Поста принадлежит функция 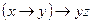 .
.
Решение.
Строим таблицу истинности.
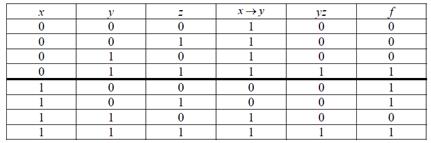
С помощью таблицы выясняем, что 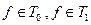 .
.
Для проверки на самодвойственность сделаем поворот и инверсию последнего столбика:
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
Первый и последний столбик не совпали, значит 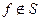 .
.
Проверяем на монотонность. Для этого сравниваем с первым набором все нижестоящие и для тех, что 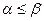 , проверяем, что
, проверяем, что 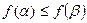 . Затем сравниваем наборы, стоящие под вторым, потом под третьим и так далее по всей таблице. Это условие не выполнено для пятого и седьмого набора:
. Затем сравниваем наборы, стоящие под вторым, потом под третьим и так далее по всей таблице. Это условие не выполнено для пятого и седьмого набора: 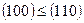 ,
, 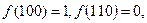
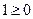 . Значит
. Значит 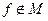 .
.
Для проверки на линейность найдем многочлен Жегалкина.
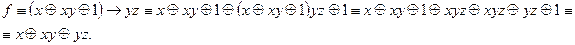
Значит 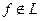 .
.
Ответ: 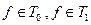 ,
, 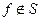 ,
, 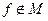 ,
, 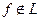 .
.
Пример №2. Проверить множество булевых функций на полноту:
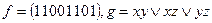 .
.
Заполним таблицу Поста.
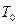
| 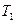
| S | L | M | |
| f | – | + | – | – | – |
| g | + | + | + | – | + |
Для первой функции составим многочлен Жегалкина методом неопределенных коэффициентов. Остальные классы проверяются по таблице истинности.
| x | y | z | f | f * | |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 |
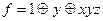 .
.
Для второй функции сначала заполним таблицу истинности:
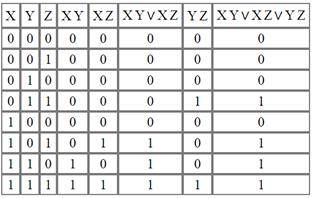 .
.
По ней определяем принадлежность классам. Многочлен Жегалкина будет иметь вид: 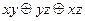 .
.
Система функций не является полной, так как обе функции принадлежат классу 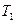 .
.
Ответ: не полная.
Задания для совместного решения.
1. Выяснить, каким классам Поста принадлежит функция:
| Ответ | |||||||
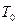
| 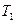
| S | L | M | |||
| а | 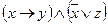
| а | – | + | – | – | – |
| б | 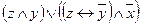
| б | + | + | + | – | – |
| в | 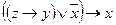
| в | + | + | + | + | + |
| г | 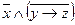
| г | + | – | – | – | – |
| д | 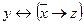
| д | – | + | – | – | – |
2. Выясните, является ли система булевых функций 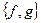 полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
| f | g | Ответ | ||
| а | 00110011 | 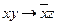
| а | полная |
| б | 10110101 | 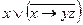
| б | не полная |
| в | 11001010 | 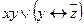
| в | полная |
Индивидуальные контрольные задания.
1. Выяснить, каким классам Поста принадлежит функция.
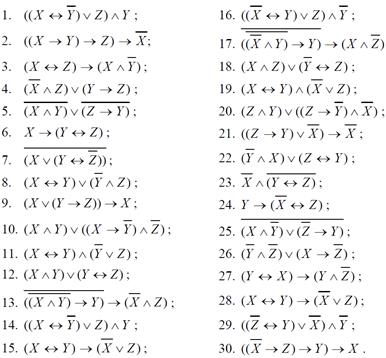
2. Выясните, является ли система булевых функций 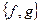 полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
| f | g | f | g | ||
| 1 | 10101100 | 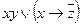
| 16 | 01000100 | 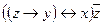
|
| 2 | 00000110 | 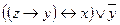
| 17 | 11111011 | 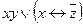
|
| 3 | 11100011 | 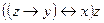
| 18 | 11000001 | 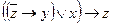
|
| 4 | 00100111 | 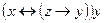
| 19 | 00110100 | 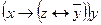
|
| 5 | 10101010 | 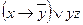
| 20 | 10010010 | 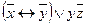
|
| 6 | 01010101 | 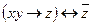
| 21 | 00001110 | 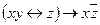
|
| 7 | 01001010 | 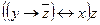
| 22 | 01110001 | 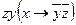
|
| 8 | 00100010 | 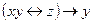
| 23 | 10001110 | 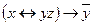
|
| 9 | 11011111 | 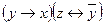
| 24 | 01111110 | 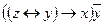
|
| 10 | 00011011 | 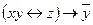
| 25 | 10000001 | 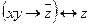
|
| 11 | 11111100 | 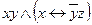
| 26 | 00110001 | 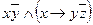
|
| 12 | 01110001 | 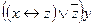
| 27 | 11001111 | 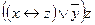
|
| 13 | 01101110 | 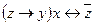
| 28 | 10010011 | 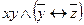
|
| 14 | 11010101 | 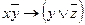
| 29 | 00100110 | 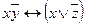
|
| 15 | 01100100 | 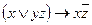
| 30 | 00010001 | 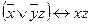
|
Практическая работа №9. Контрольная работа №1
Индивидуальные контрольные задания.
1. Функция задана формулой. Найти:
а) таблицу истинности;
б) ДНФ и КНФ;
в) СДНФ и СКНФ;
г) МДНФ;
д) РКС с минимальным числом элементов, имеющих функцию проводимости, аналогичную данной функции;
е) Каким классам Поста принадлежит данная функция?
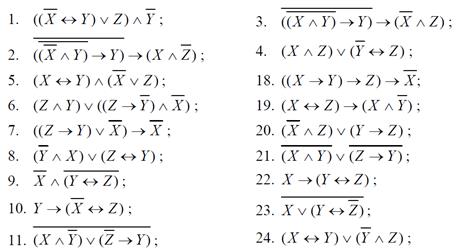
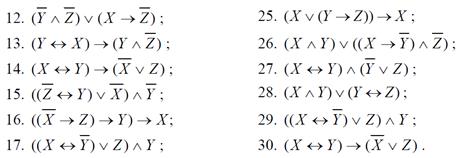
Раздел 2. Элементы теории множеств
Тема 2.1. Основы теории множеств
Практическая работа №10. Множества и основные операции над ними. Графическое изображение множеств на диаграммах Эйлера-Венна.
Дата: 2018-12-28, просмотров: 1414.