Понятие предиката. Логические операции над предикатами.
Кванторы существования и общности. Построение отрицаний к предикатам, содержащим кванторные операции.
В исчислении высказываний нет предметных переменных, то есть переменных, которые могут принимать нелогические значения, например, числовые. Для того чтобы в логические исчисления могли быть включены нелогические константы и переменные, вводится понятие предиката.
n-местным предикатом на множестве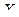 
называется функция, зависящая от n переменных, которая каждому набору 
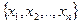ставит в соответствие один из элементов множества 
.
Пример.
1. Предикат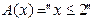 
на множестве 
– одноместный.
2. Предикат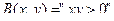 
на множестве 
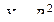– двуместный.
Если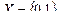 
, то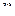 
-местный предикат представляет собой 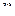-местную булеву функцию.
Нульместный предикат представляет собой высказывание.
Пример.
1. Предложение «Река х впадает в озеро Байкал» является одноместным
предикатом, определенным на множестве всех названий рек. Подставив вместо предметной переменной х название «Воронеж», получим высказывание «Река Воронеж впадает в озеро Байкал». Это высказывание ложно. Подставив вместо предметной переменной х название «Баргузин», получим истинное высказывание «Река Баргузин впадает в озеро Байкал».
2. Предложение «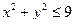 
» является двухместным предикатом, заданном на множестве 
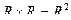. Пара действительных чисел 2 , 1 превращает данный предикат в истинное высказывание, а пара чисел 3 , 3 – в ложное высказывание.
Для каждого предиката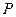 
областью истинности называется множество 
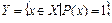, на котором предикат принимает значение 1.
Пример.1. Для предиката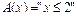 
на множестве 
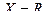область истинности 
.
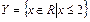2. Для предиката 
на множестве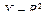 
область истинности 
.
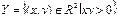Поскольку множество значений любого предиката лежит во множестве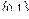 
, то с предикатами можно производить все операции алгебры логики, и все известные свойства логических операций обобщаются для предикатов. Рассмотрим эти свойства (для удобства в свойствах записываются одноместные предикаты):
1. Коммутативность:
, 
.
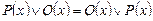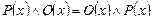2. Ассоциативность:
,
.
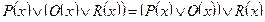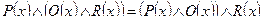3. Дистрибутивность:
,
.
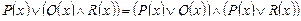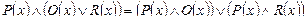1. Идемпотентность: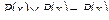 
, 
.
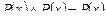2. Закон двойного отрицания: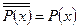 
.
3. Закон исключения третьего: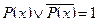 
.
4. Закон противоречия: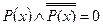 
.
5. Законы де Моргана:
,
.
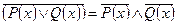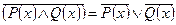6. Свойства операций с логическими константами:
, 
, 
, 
.
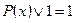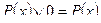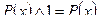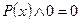Здесь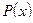 
, 
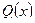и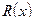 
– любые предикаты.
В то же время, для предикатов определены операции специального вида, которые называются кванторами.
Пусть дан 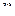-местный предикат 
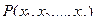на множестве 
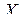, означающий, что для набора 
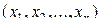выполнено свойство 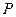, и пусть 
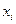– одна из переменных. Тогда запись 
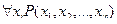означает, что для всех значений переменной 
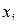свойство 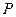выполнено. Символ 
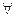называется квантором всеобщности (общности). Предикат 
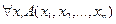является ( 
)-местным. Он зависит от переменных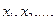 
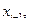
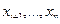. Если дан одноместный предикат 
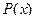, то утверждение 
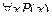представляет собой нульместный предикат, то есть истинное или ложное высказывание.
Пример. На множестве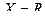 
дан предикат 
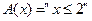. Высказывание 
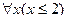ложно.
Пусть дан 
-местный предикат 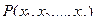на множестве 
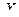, означающий, что для набора 
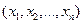выполнено свойство 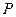, и пусть 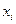– одна из переменных. Тогда запись 
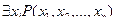означает, что существует значение переменной 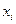, такое, что выполняется свойство 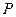. Символ 
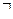называется квантором существования. Предикат 
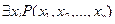является ( )-местным. Если дан одноместный предикат 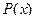, то утверждение 
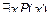представляет собой нульместный предикат, то есть истинное или ложное высказывание.
Пример. На множестве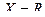 
дан предикат 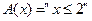. Высказывание 
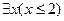истинно.
Отметим, что запись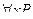 
( 
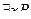) не подразумевает, что в формуле 
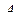есть переменная 
.
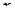Пусть дана запись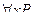 
(или 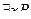). Переменная 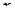называется переменной в кванторе, а 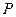– областью действия квантора.
Имеют место эквивалентности:
 .
|  .
|
 .
| 
|
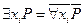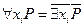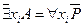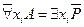
Предикат называется тождественно истинным (тождественно ложным), если при всех возможных значениях переменных он принимает значение 1(0).
Предикат называется выполнимым, если при некоторых значениях переменных он принимает значение 1.
Предикаты могут быть выражены с помощью так называемых предикатных формул. Нужно учитывать, что формула становится предикатом, когда все переменные определены на некотором множестве, и определены все предикаты, входящие в формулу.
Формула логики предикатов определяется следующим образом:
1. Любая формула логики высказываний есть формула логики предикатов.
К новым формулам логики предикатов относятся следующие выражения:
2. Предметные переменные x, y, z, ... есть формулы
3. Предикаты P(x), Q(x, y), ... , а также выражения с кванторами , ,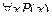 
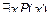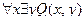, ... есть формулы.
4. Если A и B – формулы, то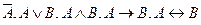 
есть формулы, в которых свободные переменные формул A и B остаются свободными, а связанные переменные формул A и B остаются связанными.
5. Ничто, кроме указанного в пунктах 1 – 4, не есть формула.
Формула, на которую распространяется действие квантора, называется областью действия квантора. Переменная, по которой навешивается квантор и попадающая в его область действия, называется связанной переменной. Переменная, лежащая вне области действия квантора, называется свободной переменной.
Область действия квантора ограничивается скобками, если она содержит более одного предиката.
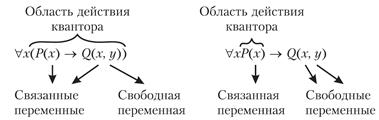
Рисунок ... – свободные и связанные переменные.
Справедливы эквивалентности:
, 
.
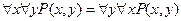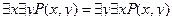Разноименные кванторы можно переставлять только следующим образом:
, 
.
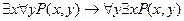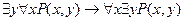Обратные формулы неверны.
Пример. Очевидно, что высказывание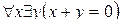 
( 
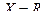) истинно. Поменяем кванторы местами. Получим высказывание 
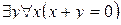, которое является ложным.
Выражения с кванторами можно преобразовывать следующим образом:
,
.
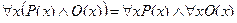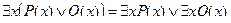Замечание. Формула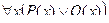 
не эквивалентна формуле 
.
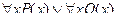Тем не менее, справедливы эквивалентности:
.
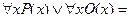
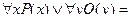
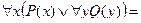
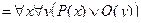Аналогично, формулы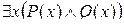 
и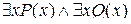 
не эквивалентны. Но справедливы эквивалентности:
.
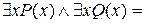
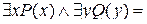
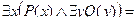
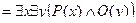Имеют место формулы:
, 
,
, 
.
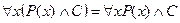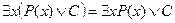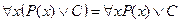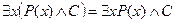Здесь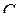 
не содержит переменной .
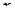Предикатная формула находится в приведенной форме, если в ней использованы только кванторные операции, а также операции инверсии, конъюнкции, дизъюнкции, причем инверсия относится только к предикатным буквам.
Предикатная формула находится в предваренной форме (предваренной нормальной форме), если она имеет вид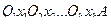 
, где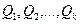 
- кванторы всеобщности или существования, а формула 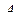находится в приведенной форме и не содержит кванторов.
Пример. Записать формулу
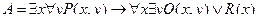
в предваренной нормальной форме.
Решение.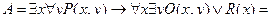 
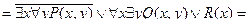
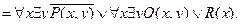
Полученная формула записана в приведенной форме. Для того чтобы квантор всеобщности можно было вынести за скобки, переобозначим переменные и выполним преобразования:
.
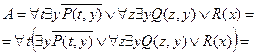
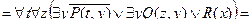
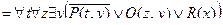С помощью предикатов можно записывать различные математические утверждения и их отрицания.
Пример. Функция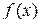 
возрастает на интервале 
.
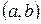Решение.
По определению возрастающей функции получим:
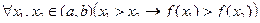
Построим отрицание:
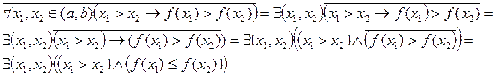
Примеры выполнения типовых заданий.
Пример №1. Установить, является ли данное выражение формулой, а если да, то определить, какие переменные в ней свободные, а какие связанные.
.
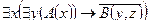Решение.
Данное выражение является формулой, так как выполнены все условия 1-5 определения формулы в алгебре предикатов.
Свободные переменные : y, z.
Связанные переменные: x.
Пример №2. Даны предикаты: А(x) и B(x): А(x) = "x – деятельность"; B(x) = "x дает счастье". Записать словами предложенные формулы С и D:
C = "x(B(x) → A(x))
D =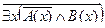 
Решение.
C = "x(B(x) →A(x)) – Счастье дается от деятельности
D =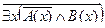
Преобразуем формулу: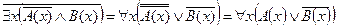 
Безделье не приносит счастье.
Пример №3. Данное суждение записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Некоторые студенты сдали все зачеты.
Решение.
Пусть A(x)=”x – студенты”, B(y)=“y – сдать все зачеты”, C(x, y)=“x – сдать все зачеты y”
тогда
$x"y(A(x)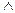 
B(y) → C(x, y)) – Некоторые студенты сдали все зачеты.
Строим отрицание:
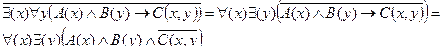
Это предложение можно прочитать следующим образом:
“Каждый студент не сдал хотя бы один зачет”.
Задания для совместного решения.
1. Установить, является ли данное выражение формулой, а если да, то определить, какие переменные в ней свободные, а какие связанные.
"x,yA(x, y).
2. Даны предикаты А(x) и B(x): А(x) = "x – наука"; B(x) = "x гуманитарная". Записать словами предложенные формулы: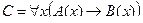 
, 
.
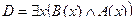3. Данное суждение записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Не все металлы твердые.
Индивидуальные контрольные задания.
1. Установить, является ли данное выражение формулой, а если да, то определить, какие переменные в ней свободные, а какие связанные.
2. Даны предикаты: А(x) и B(x). Записать словами предложенные формулы С и D.
3. Данное суждение записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
| Задание 1 | Задание 2 | Задание 3 | |
| 1 |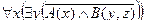 
| А(x) = "x – торговец подержанными автомобилями";
B(x) = "x – нечестный человек".
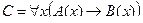
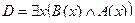
| Не всякое действительное число является рациональным |
| 2 |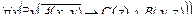 
| А(x) = "x – торговец наркотиками";
B(x) = "x – наркоман".
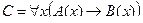
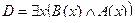
| Каждый студент выполнил хотя бы одну лабораторную работу |
| 3 |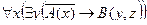 
| А(x) = "x – рациональное число";
B(x) = "x – действительное число".
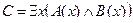
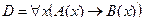
| Ни одно четное число, большее 2, не является простым. |
| 4 |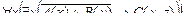 
| А(x) = "x – политик";
B(x) = "x – мошенник".
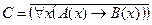
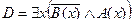
| Выгул собак или кошек запрещен. |
| 5 |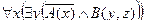 
| А(x) = "x – рыба";
B(x) = "x – водное животное".
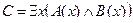
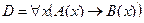
| Произведение любых двух простых чисел не является простым числом. |
| 6 |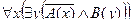 
| А(x) = "x – четное число";
B(x) = "x делится на 6".
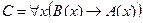
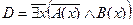
| Всякое положительное число больше всякого отрицательного числа. |
| 7 |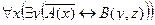 
| А(x) = "x – металл";
B(x) = "x – теплопроводен".
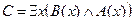
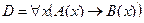
| Каждый, купивший билет, получит премию. |
| 8 |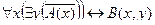 
| А(x) = "x – простое число";
B(x) = "x четное число".
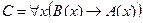
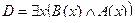
| Всякое положительное число больше всякого отрицательного числа. |
| 9 |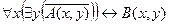 
| А(x) = "x – студент";
B(x) = "x – сдал экзамены".
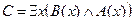
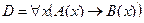
| Всякий равносторонний треугольник является равнобедренным. |
| 10 |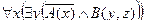
| А(x) = "x - деятельность";
B(x) = "x дает счастье".
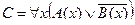
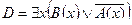
| Все студенты сдали все зачеты. |
| 11 |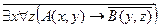 
| А(x) = "x – ученый";
B(x) = "x – мыслит формулами".
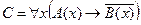
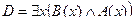
| Все депутаты голосовали за этот законопроект. |
| 12 |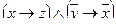 
| А(x) = "x – планета";
B(x) = "x светит собственным светом".
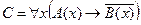
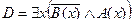
| Все рыбы живут в воде. |
| 13 |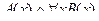 
| А(x) = "x – педагог";
B(x) = "x – учитель".
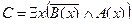
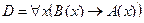
| Некоторые абитуриенты поступили в институт. |
| 14 |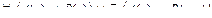 
| А(x) = "x – морское животное"; B(x) = "x дышит жабрами".
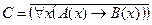
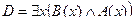
| Студент ответил на некоторые вопросы. |
| 15 |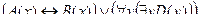 
| А(x) = "x – гриб";
B(x) = "x съедобен".
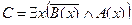
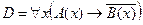
| Автобус останавливается на всех остановках. |
| 16 |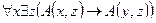 
| А(x) = "x – существительное"; B(x) = "x обозначает предмет".
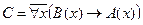
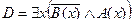
| Некоторые зрители не любят некоторых артистов |
| 17 |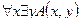 
| А(x) = "x – суждение";
B(x) = "x выражается предложением".
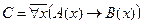
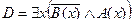
| В этой местности иногда бывает снег. |
| 18 |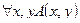 
| А(x) = "x – наука";
B(x) = "x гуманитарная".
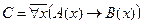
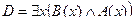
| Не все металлы твердые. |
| 19 |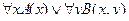 
| А(x) = "x – газ";
B(x) = "x бесцветный".
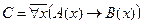
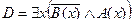
| Некоторые студенты получают стипендию. |
| 20 |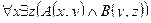 
| А(x) = "x – пассажир";
B(x) = "x платит за проезд".
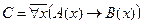
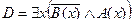
| Некоторые книги полезны. |
| 21 |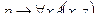 
| А(x) = "x – товар";
B(x) = "x ввозится контрабандным путем".
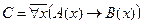
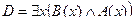
| Существуют непрерывные функции, которые не являются дифференцируемыми. |
| 22 |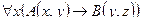 
| А(x) = "x – пошлина";
B(x) = "x взимается с цены товара".
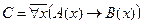
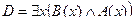
| Он ничего не знает. |
| 23 |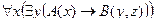 
| А(x) = "x – человек";
B(x) = "x знает, кто такой Альфред Брем".
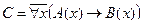
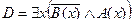
| Некоторые пассажиры не платят за проезд. |
| 24 |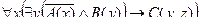 
| А(x) = "x насекомое";
B(x) = "x беспозвоночное".
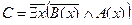
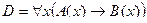
| Не все полезное приятно. |
| 25 |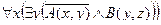 
| А(x) = "x – рыба";
B(x) = "x дышит жабрами".
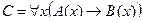
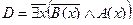
| Не всякий газ бесцветен. |
| 26 |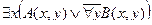 
| А(x) = "x – алгоритм";
B(x) = "x сходится".
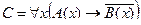
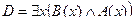
| Все люди хорошие. |
| 27 |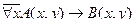 
| А(x) = "x – издательство";
B(x) = "x выпускает учебники".
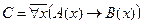
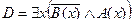
| Некоторые студенты досрочно сдали экзамены. |
| 28 |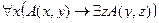 
| А(x) = "x – целое число";
B(x) = "x – рациональное число ".
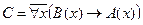
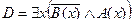
| Не все государства подписали это соглашение. |
| 29 |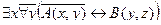 
| А(x) = "x –осёл";
B(x) = "x упрям".
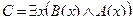
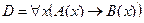
| Не все спортсмены участвовали в соревновании. |
| 30 |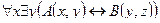 
| А(x) = "x – дерево";
B(x) = "x лиственное".
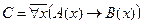
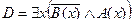
| Некоторые автобусы не останавливаются на этой остановке. |
Раздел 4. Элементы теории графов
Тема 4.1. Основы теории графов
Практическая работа №14, 15. Неориентированные и ориентированные графы.
Дата: 2018-12-28, просмотров: 651.
