Самая простая форма индексов – индивидуальные, т.к. они являются обычными относительными величинами и представляют собой соотношение двух уровней индексируемой величины.

Индивидуальный индекс показывает, во сколько раз индексируемая величина изменилась в отчетном периоде по сравнению с базисным периодом.

В зависимости от экономического назначения индивидуальные индексы бывают: физического объема продукции, себестоимости, цен, трудоемкости и т.д.

Например, индивидуальный индекс физического объема продукции рассчитывается по формуле:

.

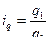Индекс физического объема показывает во сколько раз увеличился или уменьшился выпуск какого-то одного товара в отчетном периоде в сравнении с базисным.

Сводные (общие) индексы характеризуют изменение всех элементов сложного явления.

Методика их расчета зависит от характера индексируемого показателя, качеств исходных даннях и целей исследования.

Сводные индексы рассчитываются двумя способами:

- как агрегатные;

- как средние из индивидуальных.

Средние индексы, в свою очередь, рассчитываются как средние арифметичесике и средние гармонические.

Но основной формой сводных индексов является агрегатная.

В числителе и знаменателе агрегатных индексов представлены несопоставимые элементы индексируемой величины. Для обеспечения сопоставимости при расчете используются специальные показатели – соизмерители (веса) индексов.

Т.е. агрегатный индекс строится как отношение сумм произведений индексируемой величины и показателя-соизмерителя:

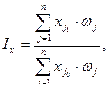
где - текущее и базисное значения индексируемой величины j-ого элемента;

 - показатель – соизмеритель явления j-ого элемента;

n – число элементов явления.

Показатель-соизмеритель может относиться либо к текущему периоду, либо к базисному.

Если к текущему, то формула имеет вид:

.

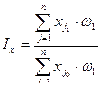Эта формула была предложена в 1874 г. Пааше и носит название: агрегатная форма индекса Пааше.

Если к базисному, то формула имеет вид:

.

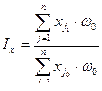Эту формулу называют агрегатной формой индекса Ласпейреса (была предложена в 1864 г. Ласпейресом).

При выборе формы агрегатного индекса необходимо решить 3 вопроса:

1. Выбрать индексируемую величину.

2. Определить состав разнородных элементов, по которым рассчитывается индекс.

3. Выбрать показатель-соизмеритель индексируемой величины (ее вес).

Выбор соизмерителя индексируемой величины определяется ее характером (содержанием).

При построении агрегатного индекса количественного (объемного) показателя соизмерителем выступает качественный показатель, при построении агрегатного индекса качественного показателя соизмерителем является количественный (объемный) показатель.

Например, агрегатный индекс стоимости продукции (объемный показатель) определяется по формуле:

.

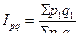Этот индекс показывает во сколько раз увеличилась (уменшилась) стоимость продукции отчетного периода в сравнении с базисным.

Разность числителя и знаменателя индекса ( S q₁p₁- S q₀p₀ ) показывает абсолютный прирост результативного показателя.

Численное значение индекса стоимости продукции определяется двумя факторами:

- изменением количества (объема) товара;

- изменением цен.

Для того, чтобы оценить изменение стоимости только за счет одного фактора, необходимо устранить влияние другого фактора. Это можно сделать, если зафиксировать в формуле данный фактор неизменным, т.е. на уровне одного и того же периода (т.е. используя индексы Пааше и Ласпейреса).

Если целью анализа является определение экономическго эффекта (прибыль, убуток) от изменения цен в отчетном периоде по сравнению с базисным, то используется индекс Пааше.

Если целью анализа является прогнозирование объема продаж в связи с возможным изменением цен в предстоящем периоде, то используется индекс Ласпейреса.

Численное значение индекса, рассчитанное по формуле Пааше всегда выше, чем рассчитанное по формуле Ласпейреса.

Как правило, для индексов качественных показателей весовой показатель принимается на уровне отчетного периода, для индексов количественных показателей – на уровне базисного периода.

К агрегатным индексам качественных показателей относятся:

- агрегатный индекс цен (Ір);

- агрегатный индекс себестоимости (Іz);

- агрегатный индекс трудоемкости (Іt);

- агрегатный индекс производительности труда (Іw).