Эмпирические кривые распределения, построенные на основе, как правило, небольшого числа наблюдений очень трудно описать аналитически, поэтому для выявления статистических закономерностей, сравнения и обобщения различных совокупностей используются теоретические распределения.

Теоретические распределения – это хорошо изученные в теории распределения, представляющие собой зависимости между плотностями распределения и значениями признака, отражающие закономерности распределения.

Теоретическая кривая распределения – кривая, которая отображает общую закономерность данного типа распределения в чистом виде, т.е. за исключением случайных факторов.

Например, распределение работников на предприятии по уровню заработной платы отображает выполнение нормативной выработки, квалификацию, расценки. Кроме того, на фактическое распределение заработной платы влияют и случайные причины (болезни, семейные обстоятельства).

Исследование формы распределения предполагает замену эмпирического распределения известным теоретическим, близким ему по форме. При этом необходимо соблюдать условие: различия между эмпирическим и теоретическим распределениями должны быть минимальными.

В статистике наиболее широко используют следующие теоретические распределения:

1. Биномиальное распределение – для описания распределения дискретного альтернативно признака. Оно представляет собой распределение вероятности исходов события, которые можно оценить как положительные

2. Распределение Пуассона – для изучения маловероятных событий в большой серии независимых испытаний (объем совокупностей n больше 100, доля единиц, обладающих данным признаком меньше 0,1).

Вероятность появления таких событий подчиняется закону Пуассона – «закону редких событий». Распределение Пуассона обычно применяется в статистическом контроле качества в массовом производстве.

3. Распределение Максвелла применяется при исследовании признака, для которого заранее известно, что распределение имеет положительную асимметрию.

Чаще всего распределение Максвелла используется при описании технологических характеристик производственных процессов.

4. Распределение Стьюдента применяют для описания распределения ошибок в малых выборках ( n меньше 30).

Распределение Стьюдента используется только при оценке ошибок выборок взятых из генеральной совокупности с нормальным распределением признака.

5. Нормальное распределение (распределение Гаусса) применяется для описания распределения признаков, на которые действуют множество независимых факторов, среди которых нет доминирующих.

При выборе теоретического распределения рассчитывают критерии согласия. Критерии согласия, опираясь на установленный закон распределения, дают возможность установить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными (случайными), а когда – существенными (неслучайными). Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой гипотезы о характере распределения в эмпирическом ряду и дать ответ, можно ли принять для данного эмпирического распределения модель, выраженную некоторым теоретическим законом распределения.

    Существует ряд критериев согласия, но чаще всего применяют критерии Пирсона χ², Колмогорова и Романовского.

    Критерий согласия Пирсона χ²  – один из основных критериев согласия, рассчитываемый по формуле:

,

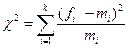где k   – число интервалов;

     f_i       – эмпирическая частота i-го интервала;

    m_i      – теоретическая частота.

Для распределения χ² составлены таблицы, где указано критическое значение критерия согласия χ² для выбранного уровня значимости α и данного числа степеней свободы ν.

    Уровень значимости α  – это вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность (P) того, что будет отвергнута правильная гипотеза. В статистических исследованиях в зависимости от важности и ответственности решаемых задач пользуются следующими тремя уровнями значимости:

1) α = 0,10, тогда P = 0,90;

2) α = 0,05, тогда P = 0,95 [1];

3) α = 0,01, тогда P = 0,99.

    Число степеней свободы ν определяется по формуле:

ν = k – z – 1,

где k   – число интервалов;

    z          – число параметров, задающих теоретический закон распределения.

Для нормального распределения z = 2, так как нормальное распределение зависит от двух параметров – средней арифметической ( 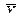) и среднего квадратического отклонения (σ).

    Для оценки существенности расхождений расчетное значение χ² сравнивают с табличным χ²_табл. Расчетное значения критерия должно быть меньше табличного, т.е. χ²<χ²_табл, в противном случае расхождения между теоретическим и эмпирическим распределением не случайны, а теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

    Использование критерия χ² рекомендуется для достаточно больших совокупностей (N>50), при этом частота каждой группы не должна быть менее 5, в противном случае повышается вероятность получения ошибочных выводов.

    Критерий Романовского К_Р основан на использовании критерия Пирсона χ², т.е. уже найденных значений χ² и числа степеней свободы ν, рассчитывается по формуле:

.

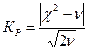Он используется в том случае, когда отсутствует таблица значений χ². Если К_Р < 3, то расхождения между теоретическим и эмпирическим распределением случайны, если К_Р > 3, то не случайны, и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

    Критерий Колмогорова λ основан на определении максимального расхождения между накопленными частотами эмпирического и теоретического распределений (D), рассчитывается по формуле:

.

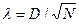Рассчитав значение λ, по таблице P(λ)  определяют вероятность, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность P(λ) может изменяться от 0 до 1. При P(λ) = 1 (т.е. при λ < 0,3) происходит полное совпадение частот, при P(λ) = 0 – полное расхождение.