Использование регрессионного и корреляционного анализа предполагает, чтобы все признаки были количественно измерены. Методы корреляционно-регрессионного анализа, основанные на использовании количественных параметров распределения (средние величины, дисперсии), называют параметрическими методами.
Проблему оценки тесноты связи между атрибутивными признаками решают непараметрические методы. Сфера их использования значительно шире, т.к. не требуется использования условия нормального распределения результативной переменой.
Для определения тесноты связи двух качественных признаков, каждый из которых состоит из двух групп, используют коэффициенты ассоциации Д.Юла и контингенции К.Пирсона.
Коэффициент ассоциации Ка определяется по формуле:
,
Коэффициент контингенции определяется по формуле:
.
Для определения этих коэффициентов не обходимо построить так называемую «таблицу четырех полей».
| а | b | a+b |
| с | d | c+d |
| а+с | b+d | a+b+c+d |
Коэффициент контингенции изменяется от +1 до -1, но всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Ка 
0,5 або Кк 0,3.
Например, нужно оценить наличие связи между работниками строительной организации, разделенными по полу и содержанию работы. Для этой цели был проведен анализ «Исследование социальных аспектов трудовой деятельности работников строительных организаций». Результаты исследования представлены в табл. 8.2.
Таблица 8.2
Распределение работников по полу и оценке содержания работы
| Работа | Мужчины | Женщины | Всего |
| Интересная Неинтересная | 300 (а) 130 (с) | 201 (b) 252 (d) | 501 (a+b) 381 (c+d) |
| Всего | 430 (a+c) | 453 (b+d) | 883 (a+b+c+d) |
В данном примере коэффициент ассоциации будет равен:
.
Связь подтверждена.
Для определения связи между количественными или качественными признаками при условии, что значения этих признаков проранжированы по степени убывания или возрастания признака, может быть использован коэффициент Спирмена, который рассчитывается по формуле:
,
де 
- квадрат разности рангов;
n - число наблюдений (число пар рангов).
Когда каждый из качественных признаков состоит более чем из двух групп, для определения тесноты связи можно использовать коэффициент взаимной спряженности (согласованности) К.Пирсона, который рассчитывается по формуле:
,
де 
- показатель взаимной спряженности.
Расчет коэффициента взаимной спряженности производится по такой схеме (табл.8.3).
Таблица 8.3
Схема расчета коэффициента взаимной спряженности
| Группы признака А | Группы признака В | Всего | ||
| В1 | В2 | В3 | ||
| А1 А2 А3 Всего | f1 f4 f7 m1 | f2 f5 f8 m2 | f3 f6 f9 m3 | n1 n2 n3 |
Аскет производится следующим образом:
по первой строчке: 
;
по второй строчке: 
;
по третьей строчке: 
;
.
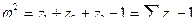Например, исследуем связь между себестоимостью продукции и накладными затратами на реализацию (табл.8.4).
Таблица 8.4
| Накладные затраты | Себестоимость | Всего nі |
| zi | ||||||||
| низкая | средняя | высокая | ||||||||||
| fi | fi2 | fi2/30 | fi | fi2 | fi2/40 | fi | fi2 | fi2/50 | ||||
| Низкие Средние Высокие | 19 7 4 | 361 49 16 | 12,03 1,63 0,53 | 12 18 10 | 144 324 100 | 3,6 8,1 2,5 | 9 15 26 | 81 225 676 | 1,62 4,5 13,5 | 40 40 40 | 17,25 14,23 16,53 | 0,431 0,356 0,413 |
| Всего | 30 | 40 | 50 | 120 | 1,2 | |||||||
По данным таблицы:
;
.
Достаточно высокое значение С указывает на наличие связи между исследуемыми признаками
Коэффициент знаков (коэффициент Фехнера) рассчитывается на основе определения знаков отклонений вариантов двух взаимосвязанных признаков от их средних величин.
Если число совпадений знаков обозначить через а, число несовпадений – через b, то этот коэффциент определяется по формуле:
.
МОДУЛЬ 3. МЕТОДЫ ИССЛЕДОВАНИЯ ПОКАЗАТЕЛЕЙ СТАТИСТИЧЕСКОГО АНАЛИЗА СОЦИАЛЬНО – ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ
Дата: 2018-12-28, просмотров: 410.
