| Вид выборочного наблюдения | Повторный отбор | Безповторный отбор |
| Случайная и механическая выборки: а) при определении среднего раз мера признака б) при определении доли признака Типичная выборка: а) при определении среднего раз мера признака б) при определении доли признака Серийная выборка: а) при определении среднего раз мера признака б) при определении доли признака | 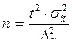
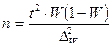
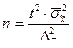
 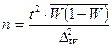
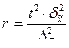
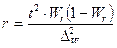
| 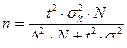
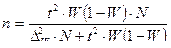
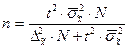
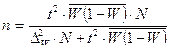
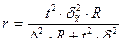
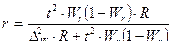
|
Вариация ( 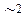 ) значений признака к началу выборочного наблюдения как правило неизвестна, поэтому ее находят приближенно одним из способов:
) значений признака к началу выборочного наблюдения как правило неизвестна, поэтому ее находят приближенно одним из способов:
1) из предыдущих выборочных наблюдений;
2) по правилу «трех сигм», согласно которому в размахе вариации укладывается примерно 6 стандартных отклонений 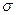 (H/
(H/ 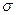 = 6, отсюда
= 6, отсюда 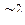 = Н2 /36);
= Н2 /36);
3) если приблизительно известна средняя величина изучаемого признака, то 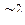 =
= 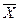 2 /9;
2 /9;
4) если неизвестна дисперсия доли единиц, обладающих каким-либо значением признака, то используется ее максимально возможная величина 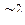 = 0,25.
= 0,25.
Пример. На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц (табл.9.4.):
Таблица 9.4.
Результаты бесповторного выборочного наблюдения на предприятии
| Доход, у.е. | до 300 | 300-500 | 500-700 | 700-1000 | более 1000 |
| Число рабочих | 8 | 28 | 44 | 17 | 3 |
С вероятностью 0,950 определить:
1) среднемесячный размер дохода работников данного предприятия;
2) долю рабочих предприятия, имеющих месячный доход более 700 у.е.;
3) необходимую численность выборки при определении среднемесячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е.;
4) необходимую численность выборки при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.
Решение. Для расчета обобщающих характеристик выборки построим вспомогательную таблицу 9.5.
Таблица 9.5.
Вспомогательные расчеты для решения задачи
| X | f | Х ’ | X’f | (Х’ - 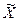 )2 )2
| (Х ’ - 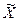 )2f )2f
|
| до 300 | 8 | 200 | 1600 | 137641 | 1101128 |
| 300 - 500 | 28 | 400 | 11200 | 29241 | 818748 |
| 500 - 700 | 44 | 600 | 26400 | 841 | 37004 |
| 700 - 1000 | 17 | 850 | 14450 | 77841 | 1323297 |
| более 1000 | 3 | 1150 | 3450 | 335241 | 1005723 |
| Итого | 100 | 57100 | 4285900 |
Рассчитаем средний доход в выборке:
= 57100/100 = 571 (у.е.).
Определим дисперсию среднего выборочного дохода:
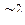 = 4285900/100 = 42859.
= 4285900/100 = 42859.
Теперь можно определить среднюю ошибку выборки :
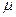 =
= 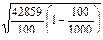 = 19,640 (у.е.).
= 19,640 (у.е.).
В нашем примере 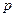 = 0,950, значит t = 1,96. Тогда предельная ошибка выборки:
= 0,950, значит t = 1,96. Тогда предельная ошибка выборки:
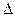 = 1,96*19,64 = 38,494 (у.е.).
= 1,96*19,64 = 38,494 (у.е.).
Для определения средней ошибки выборки при определении доли рабочих с доходами более 700 у.е. в генеральной совокупности необходимо определить их долю: w = 20/100 = 0,2 или 20%, а затем ее дисперсию по формуле 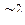 = w (1- w ) = 0,2*(1–0,2) = 0,16.
= w (1- w ) = 0,2*(1–0,2) = 0,16.
Тогда можно рассчитать среднюю ошибку выборки:
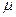 =
= 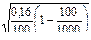 = 0,038 или 3,8%.
= 0,038 или 3,8%.
А затем и предельную ошибку выборки:
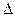 = 1,96*0,038 = 0,075 или 7,5%.
= 1,96*0,038 = 0,075 или 7,5%.
Доверительный интервал среднего дохода:
571-38,494 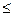
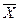
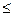 571+38,494 или 532,506 у.е.
571+38,494 или 532,506 у.е. 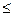
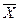
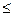 609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.
609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.
Аналогично определяем доверительный интервал для доли:
0,2-0,075 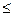 p
p 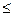 0,2+0,075 или 0,125
0,2+0,075 или 0,125 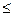 p
p 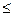 0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.
0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.
В нашей задаче выборка бесповторная, значит, воспользуемся формулой для бесповторной выборки, в которую подставим уже рассчитанные дисперсии среднего выборочного дохода рабочих ( 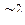 = 42859) и доли рабочих с доходами более 700 у.е. (
= 42859) и доли рабочих с доходами более 700 у.е. ( 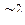 = 0,16):
= 0,16):
n б/повт = 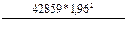 = 62 (чел.),
= 62 (чел.),
n б/повт = 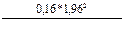 = 197 (чел.).
= 197 (чел.).
Таким образом, необходимо включить в выборку не менее 62 рабочих при определении среднего месячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е., и не менее 197 рабочих при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.
Дата: 2018-12-28, просмотров: 663.