При анализе ряда динамики возникает задание изучить его основную тенденцию (тренд). Это необходимо при изучении сезонных колебаний и при прогнозировании развития данного явления на будущее.
Тенденция (тренд) – это направление развития определенного явления. Выявить общую тенденцию развития, значит установить в каком направлении (увеличения или уменьшения) и в какой зависимости (линейной или нелинейной) она изменяется.
Динамика ряда включает 3 компонента:
- тенденцию (продолжительное движение);
- кратковременное систематическое движение (сезонное);
- несистематическое случайное движение.
При исследовании, как правило, изучают основную закономерность развития явления, которая свободна от действия разных случайных факторов. Для этого ряды динамики и специальным образом обрабатывают – выравнивают.
К способам и методам выравнивания динамических рядов относят:
- укрупнение интервалов;
- расчет средних уровней для укрупненных интервалов;
- определение скользящей средней;
- аналитическое выравнивание.
Наиболее простым способом выравнивания рядов является укрупнение их интервалов. Суть этого метода состоит в том, что первичный ряд динамики заменяется другим, уровни которого относятся к большим по продолжительности периодам времени.
Например, имеются данные о реализации товаров по месяцам, тыс.р.:
| январь | 100 |
370 |
| февраль | 150 | |
| март | 120 | |
| апрель | 110 |
390 |
| май | 180 | |
| июнь | 100 | |
| июль | 90 |
410 |
| август | 200 | |
| сентябрь | 120 | |
| октябрь | 160 |
430 |
| ноябрь | 140 | |
| декабрь | 130 |
После укрупнения интервалов тенденция увеличения реализации товаров становится явной:
370 <390<410<430
Частным случаем рассмотренного способа является расчет средних уровней для укрупненных интервалов. При этом укрупненные уровни ряда динамики заменяются средними уровнями укрупненных интервалов:
370:3 =128,3; 390:3=130; 410:3=136,7; 430:3=143,3.
При этом также явно прослеживается тенденция увеличения реализации товаров:
128,3<130<136,7<143,3.
Суть метода скользящей средней состоит в том, что для первичного ряда динамики формируются укрупненные интервалы, которые состоят из одинакового количества уровней m. Каждый последующий интервал получается последовательным смещением от начального на 1 уровень.
Затем для новых интервалов рассчитываются средние уровни:
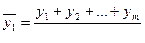 ;
; 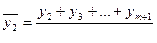 .
.
Например.
Таблица 11.1
| Рабочие дни декады | Выпуск продукции, млн.р. | Изменяющиеся суммы | Скользящие средние | ||
| 3-х дневные | 5-ти дневные | 3-х дневные | 5-ти дневные | ||
| 1 | 37 | - | - | - | - |
| 2 | 42 | 112 | - | 37,3 | - |
| 3 | 33 | 120 | 215 | 40 | 43 |
| 4 | 45 | 136 | 233 | 45,3 | 46,6 |
| 5 | 58 | 158 | 247 | 52,7 | 49,4 |
| 6 | 55 | 169 | 284 | 56,3 | 56,8 |
| 7 | 56 | 181 | 308 | 60,3 | 61,6 |
| 8 | 70 | 195 | 324 | 65 | 64,8 |
| 9 | 69 | 213 | 324 | 71 | 64,8 |
| 10 | 74 | 214 | - | 71,3 | - |
| 11 | 71 | - | - | - | - |
Использование в анализе рядов динамики рассмотренных способов позволяет выявить тренд для описания, но получить обобщающую статистическую оценку тренда с помощью этих способов невозможно.
«Измерить» тренд можно с помощью аналитического выравнивания.
Суть аналитического выравнивания динамических рядов состоит в том, что фактические уровни ряда изменяются плавно и уровни рассчитываются на основе определенной прямой или кривой, которые точнее всего отображает тенденцию явления.
В основе этого метода лежит установление функциональной зависимости с помощью корреляционно-регрессионного анализа.
Например. Произведем аналитическое выравнивание ряда динамики по прямой  (табл. 11.2).
(табл. 11.2).
Таблица 11.2
| Годы | Объем производства строительных материалов, тыс.т. | Условные обозначения периодов,t | 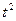
| 
| 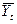
| 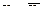
| 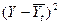
|
| 2011 | 15,5 | -2 | 4 | -31 | 15,18 | 0,3 | 0,09 |
| 2012 | 15,1 | -1 | 1 | -15,1 | 15,31 | -0,21 | 0,044 |
| 2013 | 15,2 | 0 | 0 | 0 | 15,44 | -0,2 | 0,04 |
| 2014 | 15,4 | 1 | 1 | 15,4 | 15,57 | -0,2 | 0,04 |
| 2015 | 16,0 | 2 | 4 | 32 | 15,7 | 0,3 | 0,09 |
| Всего | 77,2 | 0 | 10 | 1,3 | 77,2 | 0,304 |
Если число уровней ряда динамики парное, то t можно представить как -3;-2;-1;+1;+2;+3, чтобы t =0.
Система нормальных уравнений для нахождения параметров линейной регрессии методом наименьших квадратов имеет такой вид:
па + b t = у;
а t + b t 2 = t у,
если t =0, то у= па, следовательно а= у/п
t у= b t 2,следовательно b = t у/ t 2
В нашем случае а=77,2/5=15,44
b =1,3/10=0,13
Соответственно, уравнение прямой (тренд) имеет вид:
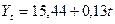 ,
,
где 0,13 означает, что среднегодовой абсолютный прирост производства строительных материалов составляет 0,13 тыс.т., а 15,44 тыс.т. – это среднегодовое производство строительных материалов.
Подставляя в уравнение тренда принятые значения t получим:
2011 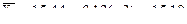 ,
,
2012 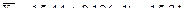 и т.д.
и т.д.
По окончанию расчета основной тенденции целесообразно изобразить графически выходные и теоретические уровни.
Основная тенденция (тренд) показывает, как влияют систематические факторы на уровень ряда динамики, а колебания уровней вокруг тренда являются мерой влияния остаточных факторов.
Показатель колебаний рассчитывается по формуле среднеквадратического отклонения:
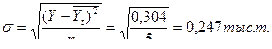
Коэффициент вариации:
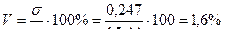
Выравнивание рядов динамики используется для того, чтобы рассчитать значение отсутствующего члена ряда. Эта процедура называется интерполяция. Для прогнозирования экономических показателей используется экстраполяция, т.е. продолжение в будущем тенденций, которые наблюдались в прошлом. При этом значения t за границами динамического ряда подставляют в трендовое уравнение и получают прогнозное значение уровня тренда в будущем.
Дата: 2018-12-28, просмотров: 677.