1. Виды связей между явлениями.
2. Регрессионный анализ.
3. Корреляционный анализ.
4. Анализ связи между атрибутивными признаками.
Виды связей между явлениями.
Все социально-экономические явления взаимосвязаны и зависимость между ними носит причинно-следственный характер. Суть причинно- следственной связи состоит в том, что при определенных условиях одно явление обуславливает другое и в результате такого взаимодействия возникает следствие.
Изучая закономерности связи, причины и условия, которые их характеризуют, объединяют в понятие фактора.
Признаки, которые являются причинами и условиями связи, называются факторными (х), а которые изменяются под влиянием факторных признаков – результативными (у).
Выделяют 3 вида взаимосвязей:
- факторные (изучаются с помощью метода группировок и теории корреляции);
- компонентные (изучаются с помощью индексного метода);
- балансовые (изучаются путем построения балансов).
В зависимости от статистической природы между признаками х и у существуют разные по характеру виды связи:
- функциональные;
- стохастические (вероятностные).
При функциональной связи между х и у каждому значению х соответствует одно четко определенное значение у.
При стохастической связи каждому отдельному значению факторного признака х соответствует определенное множество значений результативного признака у.
Подвидом стохастической связи является корреляционная зависимость, которая обуславливает корреляционную связь между признаками. При такой зависимости с изменением факторного признака х изменяется групповой средний результат признака у.
По своей форме корреляционные связи бывают:
- прямые (если х и у изменяются в одном направлении, т.е. ибо снижаются, либо увеличиваются) и обратные (если при увеличении х снижается у и наоборот);
- прямолинейные (выражаются уравнениями прямой) и криволинейные (выражаются уравнениями параболы, гиперболы и т.д.);
- однофакторные (если исследуется связь между одним факторным признаком х и результативным у) и многофакторные (если исследуется связь между несколькими факторными признаками х и результативным у).
Главной характеристикой корреляционной связи является линия регрессии.
Линия регрессии У(х) – это функция, которая связывает средние значения У со значениями х.
В зависимости от формы линии регрессии выделяют линейные (в виде прямой) и нелинейные связи.
В процессе корреляционно-регрессионного анализа решаются 2 задачи:
- определить теоретическую форму связи (регрессионный анализ);
- определить тесноту, статистическую значимость и надежность связи (корреляционный анализ).
Регрессионный анализ.
Изучение корреляционной связи начинается с регрессионного анализа, который решает проблему установления формы связи или вида уравнения регрессии и определения параметров уравнения регрессии.
Различают уравнения простой (парной) регрессии (когда один х соответствует у) и множественной (многофакторной) регрессии (когда результативный признак у связан с несколькими факторными признаками х).
Уравнение регрессии показывает, как в среднем изменяется у при изменении какого-либо х і и имеет вид:
У(х) = f(х 1 ,х 2 … …х n ).
Наиболее часто для характеристики корреляционной связи используют такие вид уравнений парной регрессии:
- линейное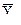 
= а0 + a1 x;
- гиперболическое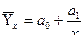 
;
- параболическое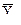 
= а0 + а1 x + а1 x2 і т.д.
где а0, а1 – параметры уравнений регрессии, которые необходимо определить.
Параметр а0 показывает усредненное влияние на результативный признак факторов, которые не учтены.
Параметр а1 показывает насколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу.
Параметры в уравнениях регрессии определяются методом наименьших квадратов, суть которого в минимизации суммы квадратов отклонений фактических значений результативного показателя от расчетных значений.
Система нормальных уравнений для нахождения параметров линейной регрессии методом наименьших квадратов имеет такой вид:
па0 + а1 x= у;
а0 x + а1 x2 = xу,
где n – объем исследуемой совокупности (число единиц наблюдения).
Например, имеются данные, характеризующие деловую активность акционерных обществ закрытого типа (АОЗТ): прибыль (млн. р.) и затраты на 1 р. произведенной продукции (коп). (табл.8.1).
Предположим наличие линейной зависимости между анализируемыми признаками. Система нормальных уравнений для данного примера имеет вид:
па0 + а1 x= у;
а0 x + а1 x2 = xу,
Подставив данные, рассчитанные в табл.8.1. получим:
6а0 + 502а1 = 4466;
502 а0 + 42280 а1 = 362404.
Таблица 8.1
Расчетные данные для определения параметров линейного уравнения регрессии
| № | Затраты на 1 р. произведенной продукции, коп. , х | Прибыль, тыс. р., у | x2 | ху | __ x |
| 1 2 3 4 5 6 | 77 77 81 82 89 96 | 1070 1001 789 779 606 221 | 5 929 5 929 5 561 6 724 7 921 9 216 | 82 390 77 077 63 909 63 878 53 934 21 216 | 1 016 1 016 853 812 527 242 |
| Итого | 502 | 4 466 | 42 280 | 362 404 | 4 466 |
Решив систему уравнений получим: а0 = 4153,88; а1 = - 40,75
Таким образом, Ух = 4153,88 - 40,75x.
Если связь между признаками х и у является криволинейной и описывается уравнением параболы второго порядка:
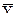= а0 + а1 x + а2 x2
задача сводится к определению неизвестных параметров: а0, а1, а2, а система нормальных уравнений имеет вид:
па0 + а1 x + а2 x2 = у;
а0 x+ а1 x2 + а2 x3 = уx;
а0 x2 + а1 x3 + а2 x4 = уx2.
Оценка обратной зависимости между х и у, когда при увеличении (уменьшении) х уменьшается (увеличивается) значение результативного признака у, может быть осуществлена на основе уравнения гиперболы:
.
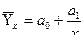Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:
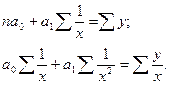
Наиболее сложным этапом, который завершает регрессионный анализ, является интерпретация уравнения, т.е. перевод его с языка статистики и математики на язык экономиста.
С целью расширения возможностей экономического анализа используется коэффициент эластичности, который определяется по формуле:
,
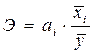где xі - среднее значение соответствующего факторного признака;
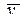- среднее значение результативного признака;
аі - коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает, на сколько процентов в бреднем изменится значение результативного признака при изменении факторного признака на 1 %.
Корреляционный анализ.
После выбора вида уравнения регрессии и нахождения его параметров приступают к оценке тесноты и значимости (существенности) связи.
Тесноту святи оценивают с помощью коэффициентов детерминации, корреляции (корреляционного отношения).
Коэффициент детерминации показывает, в какой степени вариация результативного признака у определяется вариацией факторного признака х. Он используется как при линейной, так и при нелинейной связи между признаками и в случае парной регрессии рассчитывается по формуле:
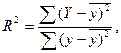
где у – фактические значения результативного признака;
У – теоретические значения результативного признака (по линии регрессии).
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе он к одинице, тем теснее связь между признаками; если коэффициент детерминации равен 0 линейная связь между показателями отсутствует; если равен 1 - не существует корреляционной связи между признаками.
Коэффициент корреляции (корреляционное отношение) показывает насколько значительным является влияние фактора х на у и рассчитывается по формуле:
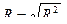
Он находится в диапазоне от 0 до1; чем ближе к единице, тем теснее корреляционная связь между признаками.
В случае линейной связи между х и у линейный коэффициент корреляции рассчитывается по формуле:
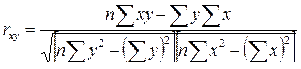
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: -1 r 1.
После установления тесноты связи дают оценку значимости связи между признаками. Под термином «значимость связи» понимают оценку отклонений выборочных переменных от своих значений в генеральной совокупности с помощью статистических критериев. Оценку значимости связи осуществляют с использованием F-критерия Фишера и t-критерия Стьюдента.
Для парной регрессии (линейной и нелинейной) F-критерий Фишера рассчитывается по формуле:
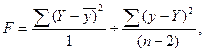
где 1, (n-2) – число степеней свободы числителя и знаменателя зависимости.
«Степень свободы» - целое число, которое показывает сколько независимых элементов информации в переменных у необходимо для суммы квадрата (это поясняет соответствующую дисперсию: общую, среднюю из групповых, межгрупповую).
Теоретическое значение F сравнивают с табличным (критическим) значением F табл, которое выбирают из справочных математических таблиц F-критерия Фишера в зависимости от степеней свободы 1, (n-2) и принятого уровня значимости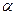 
. Чаще всего в статистико-экономических исследованиях используют такие уровни значимости, как 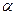=0,05 и 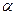=0,01. Если F> F табл, то выборочная совокупность и связь между признаками являются значительными.
Для парной линейной регрессии при r = R расчетные значения t –критерия Стьюдента определяются по формуле:
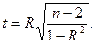
Критерий Стьюдента дает оценку значимости коэффициента корреляции R и существенности связи между признаками.
Рассчитанное по формуле теоретическое значение t –критерия Стьюдента сравнивают с табличным для соответствующего числа степеней свободы и принятого уровня значимости 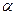. Табличное значение критерия Стьюдента выбирается из справочных математических таблиц. Если t>tтабл,то линейный коэффициент корреляции считается значимым при характеристике генеральной совокупности.
Дата: 2018-12-28, просмотров: 432.
