К характеристикам центра распределения, кроме обобщающих характеристик совокупности (средней арифметической, средней гармонической), принадлежат вспомогательные описательные характеристики распределения вариационного признака, которые называют структурными средними – мода и медиана.
Мода и медиана – это типовые характеристики в тех случаях, когда совокупности однородные и значительные по численности.
Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности.
Мода используется в тех случаях, когда нужно охарактеризовать величину признака, которая наиболее часто повторяется. Например, наиболее распространенный размер заработной платы на предприятии, цены на рынке, по которой было продано наибольшее количество товара, размер обуви, который имеет наибольший спрос среди населения.
Способ расчета моды зависит от вида статистического ряда. В атрибутивных и дискретных рядах модой является варианта, которая имеет наибольшую частоту. Например, рассмотрим распределение семей по числу детей (табл. 6.3.)
Таблица 6.3.
Распределение семей по числу детей
| Группы семей по числу детей | Число семей |
| 0 | 10 |
| 1 | 30 |
| 2 | 75 |
| 3 | 45 |
| 4 | 20 |
| 5 | 15 |
| Всего | 195 |
Модой будет группа семей, которая имеет двух детей, т.к. этому значению варианты соответствует наибольшее число семей (75).
Если в распределениях все варианты встречаются одинаково часто, они все считаются модальными. Если не одна, а две варианты имеют наибольшие частоты распределение будет бимодальным.
В интервальном ряду для определения моды вначале находят модальный интервал исследуемого ряда (интервал с наибольшей частотой). Например, рассмотрим распределение работников по размеру заработной платы (табл. 6.4.).
Таблица 6.4.
Распределение работников по размеру заработной платы
| Группы работников по размеру заработной платы, р. | Количество работников |
| 1300-1400 | 10 |
| 1400-1500 | 50 |
| 1500-1600 | 100 |
| 1600-1700 | 115 |
| 1700-1800 | 180 |
| 1800-1900 | 45 |
| Итого | 500 |
Наибольшая частота (f) соответствует интервалу, где варианта находится в границах 1700-1800. Это и будет модальный интервал.
Для расчета значения модальной величины признака, который находится в этом интервале используют зависимость:
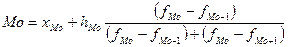
где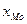 
- нижняя граница модального интервала (в нашем случае 1700); 
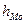- величина модального интервала (100); 
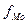- частота, соответствующая модальному интервалу (180); 
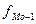- частота, предшествующая модальному интервалу (115); 
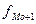-частота интервала, следующего за модальным (45).
В нашем случае (табл. 6.4):
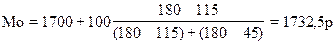
Медианой называется варианта, которая находится в середине упорядоченного вариационного ряда. Медиана делит ряд на две, равные по численности, части.
Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Для ранжированного ряда с четным числом членов медианой будет средняя арифметическая из двух смежных вариант:
.
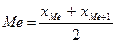В интервальном вариационном ряду порядок нахождения медианы следующий:
1. Располагаем индивидуальные значения признака ранжировано.
2. Определяем для данного ранжированного ряда накопленные (кумулятивные) частоты (путем постепенного добавления частот, начиная с интервала, который имеет наименьшее значение признака).
3. По данным о накопленных частотах находим медианный интервал (кумулятивная частота котрого равна или превышает половину суммы частот).
4. Определяем медиану по формуле:
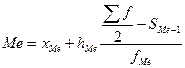
де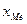 
- нижняя граница медианного интервала; 
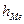- размер медианного интервала; 
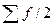- полусумма частот ряда; 
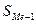- сумма накопленных частот, предшествующих медианному интервалу; 
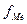- частота медианного интервала.
Рассчитаем медиану для нашего случая (табл. 6.4):
Таблица 6.5.
Расчет медианы в интервальном ряду
| Группы работников по размеру заработной платы, р. | Количество работников | Кумулятивная частота |
| 1300-1400 | 10 | 10 |
| 1400-1500 | 50 | 60 |
| 1500-1600 | 100 | 160 |
| 1600-1700 | 115 | 275 |
| 1700-1800 | 180 | 455 |
| 1800-1900 | 45 | 500 |
| Итого | 500 | - |
Половина суммы частот составляет 250 (500/2). Таким образом, медианным будет інтервал со значеним заработной платы 1600-1700. Для предыдущего интервала сумма накопленнях частот составляет 160. Значит медиана будет равна:
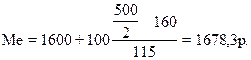
Дополнительно к медиане для характеристики вариационного ряда рссчитываются квартили (делят ряд по сумне частот на 4 равные части) и децили (делят ряд по сумне частот на 10 равных частей).
Показатели вариации
После определения средней величины встает вопрос, в какой мере индивидуальные значения признака отличаются между собой и от средней. Для этого определяют показатели вариации.
Вариацией признака называют разницу в числовых значениях признаков единиц совокупности и их колебания вокруг средней величины, которая характеризует совокупность. Чем меньше вариация, тем более однородной является совокупность и более надежной (типовой) – средняя величина.
К основным абсолютным и относительным показателям, характеризующим вариацию относятся:
- размах вариации;
- среднее линейное отклонение;
- коэффициент осцилляции;
- дисперсия;
- стандартное среднее квадратическое отклонение;
- коэффициент вариации.
Размах вариации – это разница между наибольшим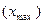 
и наименьшим 
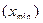значениями признака:
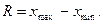
Среднее линейное отклонение – это средний модуль отклонений индивидуальных значений признака от их средней величины:
- для несгруппированных данных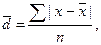 
- для сгруппированных данных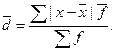 
Коэффициент осциляции – это отношение размаха вариации к среднему значению признака:
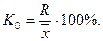
Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней величины:
- для несгруппированных даннях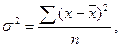 
- для сгруппированных данных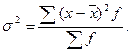 
Среднее квадратическое отклонение – это обобщающая характеристика абсолютних размеров вариации признака в совокупности.Определяется как корень квадратный из дисперсии:
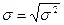
Среднее квадратическое отклонение всегда выражается в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.) и является абсолютной мерой вариации.
Чем меньше среднее квадратическое отклонение, тем более типовой является средняя и тем более однородной является совокупность.
Коэффициент вариации является относительной мерой вариации и позволяет сравнивать степень вариации признаков в рядах вариации с разным уровнем средних. Рассчитывается как отношение среднего квадратического отклонения от средней величины:
.
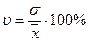Если коэффициент вариации <33 %, то такая совокупность считается однородной.
Дисперсионный анализ
Основной целью дисперсионного анализа является выявление на основе величины общей дисперсии влияния отдельных факторов на вариацию признака. Для оценки доли вариации, обусловленной тем или иным признаком, совокупность разделяют на группы по тому признаку, свойства которого исследуются. Это позволяет разложить общую дисперсию на 2 дисперсии, из которых одна часть вариации определяется влиянием фактора, который положен в основу группировки, а вторая – вариацией всех факторов, кроме того, который изучается. Т.е. соответственно с правилом сложения дисперсий, если данные представлены в виде аналитической группировки, определяют общую, межгрупповую, внутригрупповую дисперсии.
Общая дисперсия характеризует вариацию признака в статистической совокупности в результате влияния всех факторов.
Общая дисперсия для сгруппированных данных определяется по формуле:
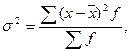
для несгруппированных даннях:
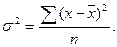
Кроме того, применяются два упрощенных способа расчета общей дисперсии:
1. Если варианты выражены небольшими числами, дисперсия определяется как разность средних:
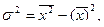
2. Если варианты выражены большими числами, то применяют способ моментов:
,
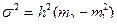где m1 – момент первого порядка;
m2 – момент второго порядка.
Межгрупповая дисперсия показывает уровень отклонения групповых средних от общей средней, т.е. характеризует влияние фактора, положенного в основу группировки:
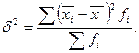
Внутригрупповая дисперсия характеризует вариацию признака в средине каждой группы статистической группировки:
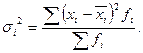
Средняя из внутригрупповых дисперсий определяется следующим образом:
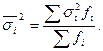
Связь между общей дисперсией, средней из групповых и межгрупповой дисперсиями можно проследить с помощью правила сложения дисперсий:
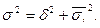
Сущность связи между признаками характеризует коэффициент детерминации, который рассчитывается как отношение межгрупповой дисперсии к общей дисперсии:
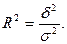
Эмпирическое корреляционное отношение – это корень квадратный из коэффициента детерминации:
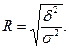
Корреляционное отношение характеризует степень приближения связи к функциональной, т.е. тесноту корреляционной зависимости и колеблется от 0 до 1.
Наряду с вариацией индивидуальных значений признака вокруг средней может наблюдаться и вариация индивидуальных долей признака вокруг средней доли. Такое изучение вариации достигается посредством вычисления и анализа следующих видов дисперсий:
- внутригрупповая: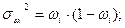 
- средняя из внутригрупповых дисперсий: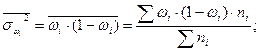 
- межгрупповая: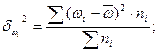 
- общая: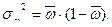 
При этом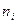 
- численность единиц в отдельных группах;
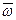- доля изучаемого признака во всей совокупности, которая определяется по формуле: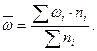 
Дата: 2018-12-28, просмотров: 430.
