1. Теорема Вейерштрасса о сходимости монотонной последовательности.
2. Теорема Больцано–Вейерштрасса о существовании сходящейся подпоследовательности.
3. Свойства фундаментальной последовательности.
4. Критерий Коши для последовательностей.
5. Теоремы Больцано–Коши о промежуточных значениях непрерывной функции.
6. Теоремы Вейерштрасса об ограниченности непрерывной функции.
7. Теорема о дифференцировании сложной функции.
8. Теорема о производной функции, заданной параметрически.
9 Теорема Ферма о необходимом условии экстремума дифференцируемой функции.
10. Теорема Ролля.
11. Теорема Лагранжа о среднем значении в дифференциальном исчислении.
II. Определения и формулировки теорем и свойств.
1. Предел последовательности.
2. Бесконечно малые (б.м.) последовательности и их свойства.
3. Свойства сходящихся последовательностей.
4. Подпоследовательность, частичные пределы.
5. Окрестность точки.
6. Два определения предела и теорема об их равносильности.
7. Бесконечно малые (б.м.) функции и их свойства.
8. Определение функций, имеющих предел и их свойства.
9. 1 и 2 замечательные пределы.
10. Определение О-большого и о-малого, эквивалентные функции.
11. Непрерывность функции в точке.
12. Классификация точек разрыва.
13. Теоремы о непрерывности монотонной, сложной и обратной функций.
14. Определение равномерной непрерывности.
15. Теорема Кантора о равномерной непрерывности.
16. Определение производной, ее геометрический и механический смысл.
17. Теорема о производной обратной функции.
18. Теорема об арифметических операциях над производными.
19. Следствие о непрерывности функции, имеющей производную.
20. Определение дифференциала, и его геометрический смысл.
21. Теорема о связи между дифференцируемостью и существованием производной.
22. Инвариантность формы первого дифференциала.
23. Следствия из теоремы Лагранжа: условие постоянства функции, условие монотонности функции.
Образец экзаменационного билета
1. Определения и формулировки теорем и свойств (матдиктант)
1. Предел последовательности.
2. 1 и 2 замечательные пределы.
3. Теорема Кантора о равномерной непрерывности.
4. Теорема о производной обратной функции.
5. Правило Лопиталя.
6. Определение локального экстремума функции.
2. Доказать методом от противного одну из перечисленных теорем:
1. Теорема Вейерштрасса о сходимости монотонной последовательности.
2. Теоремы Вейерштрасса об ограниченности непрерывной функции.
3. Теорема Лагранжа о среднем в дифференциальном исчислении.
4. Теорема Ролля.
5. Критерий Коши для последовательностей.
3. Решить
1. Найти предел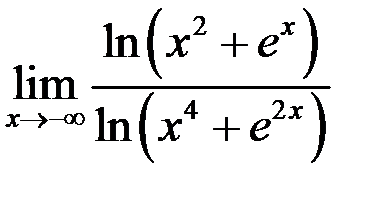 
.
2. В каких точках касательные к кривой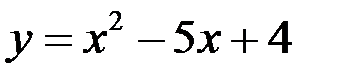 
параллельны прямой 
.
Варианты индивидуального задания
«Предел. Непрерывность»
Задание 1
1. Доказать, что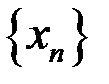 
– бесконечно малая последовательность, если: 
.
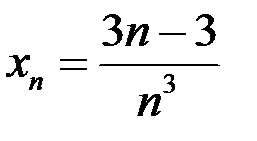2. Доказать, что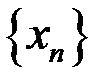 
– бесконечно малая последовательность, если: 
.
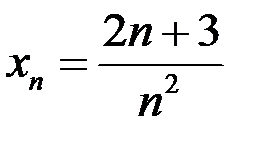3. Доказать, что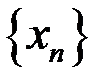 
– бесконечно малая последовательность, если: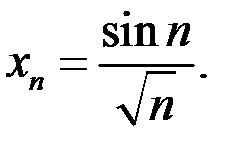 
4. Доказать, что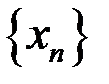 
– бесконечно малая последовательность, если: 
.
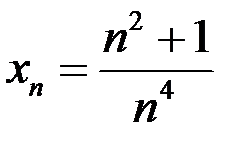5. Доказать, что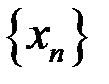 
– бесконечно малая последовательность, если: 
.
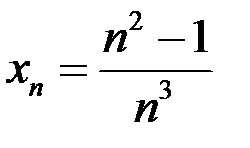6. Доказать, что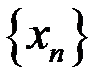 
– бесконечно малая последовательность, если: 
.
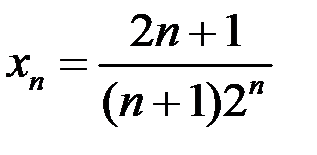7. Доказать, что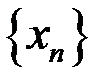 
– бесконечно малая последовательность, если: 
.
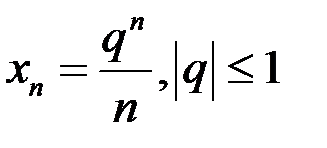8. Доказать, что 
– бесконечно малая последовательность, если: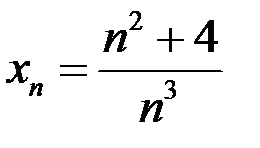 
.
9. Доказать, что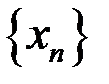 
– бесконечно малая последовательность, если: 
.
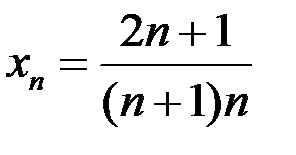10. Доказать, что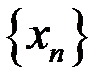 
– бесконечно малая последовательность, если: 
.
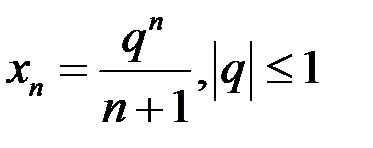Задание 2
1. Доказать, что последовательность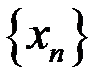 
расходится, если: 
.
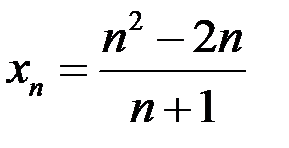2. Доказать, что последовательность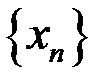 
расходится, если: 
3. Доказать, что последовательность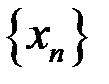 
расходится, если: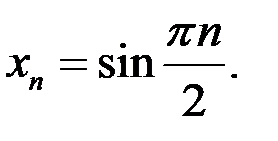 
4. Доказать, что последовательность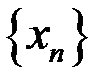 
расходится, если: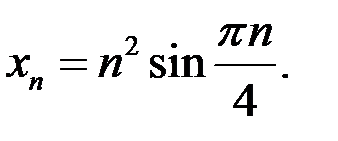 
5. Доказать, что последовательность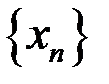 
расходится, если: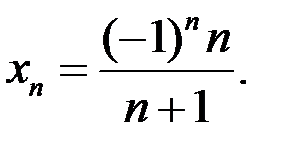 
6. Доказать, что последовательность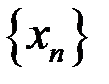 
расходится, если: 
7. Доказать, что последовательность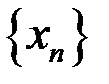 
расходится, если: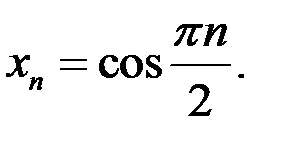 
8. Доказать, что последовательность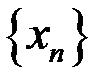 
расходится, если: 
.
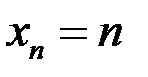9. Доказать, что последовательность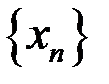 
расходится, если: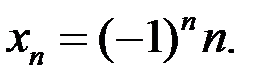 
10. Доказать, что последовательность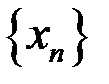 
расходится, если: 
.
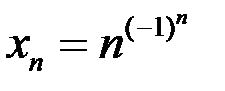Задание 3
1. Доказать, что 
.
2. Доказать, что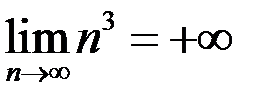 
.
3. Доказать, что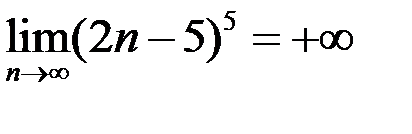 
.
4. Доказать, что 
.
5. Доказать, что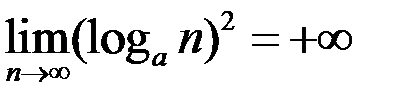 
.
6. Доказать, что 
.
7. Доказать, что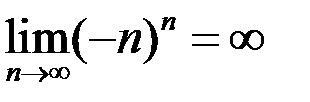 
.
8. Доказать, что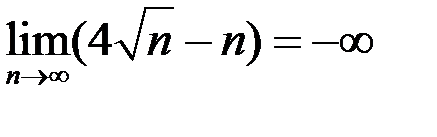 
.
9. Доказать, что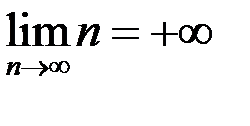 
.
10. Доказать, что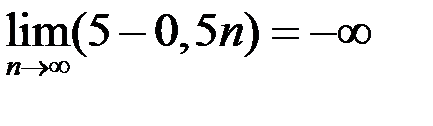 
.
Задание 4
1. Найти множество частичных пределов,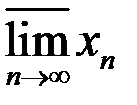 
, 
, 
, 
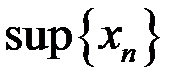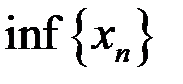для последовательностей: а) 
;
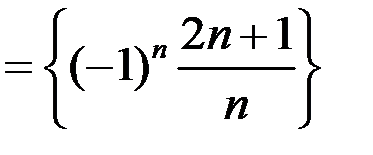б) 
.
2. Найти множество частичных пределов 
, 
, 
, 
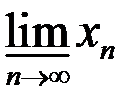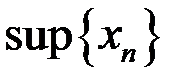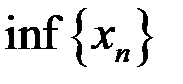для последовательностей: а)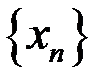 
;
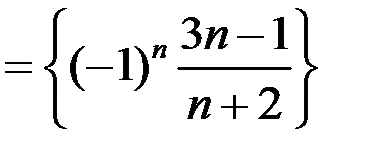б)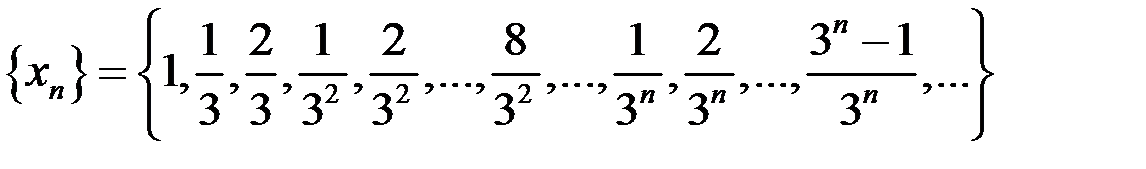 
.
3. Найти множество частичных пределов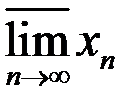 
, 
, 
, 
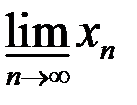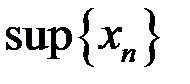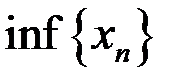для последовательностей: а) 
;
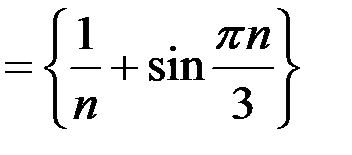б)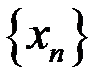 
= 
.
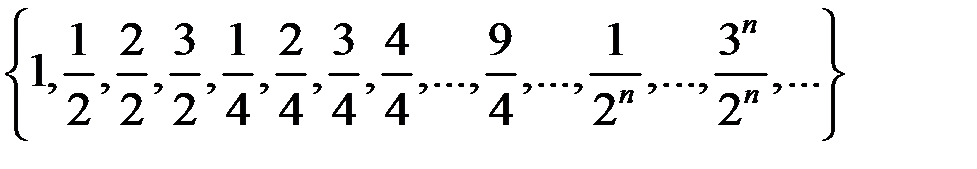4. Найти множество частичных пределов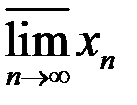 
, 
, 
, 
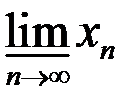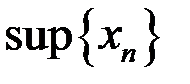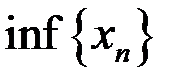для последовательностей: а)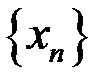 
;
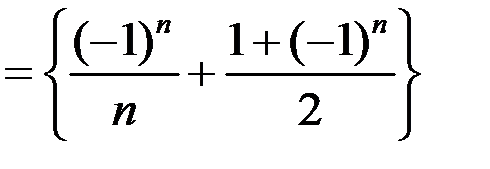б)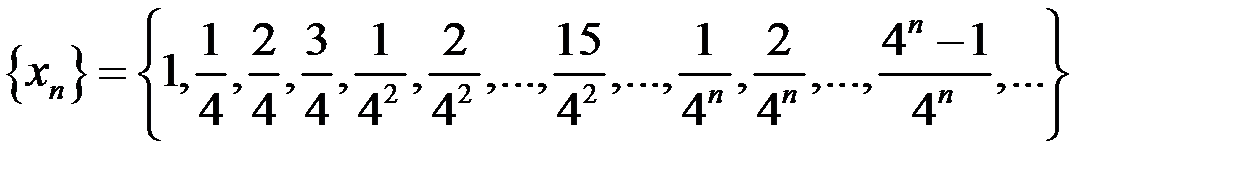 
.
5. Найти множество частичных пределов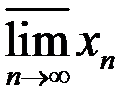 
, 
, 
, 
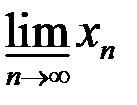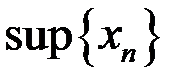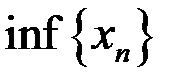для последовательностей: а) 
;
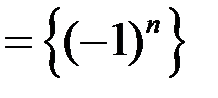б)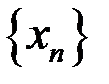 
= 
.
6. Найти множество частичных пределов 
, 
, 
, 
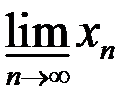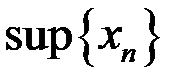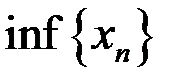для последовательностей: а)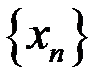 
;
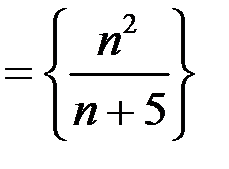б)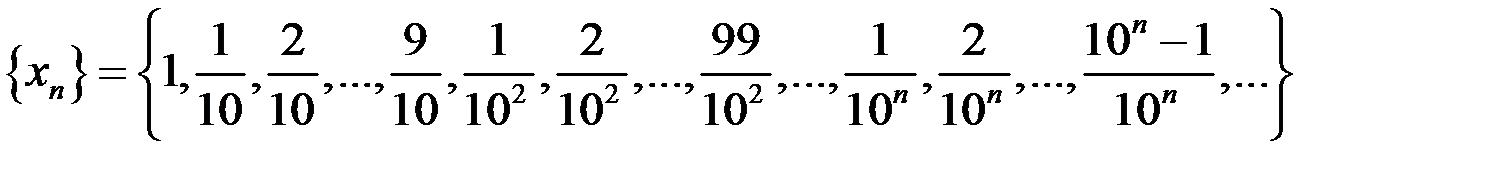 
.
7. Найти множество частичных пределов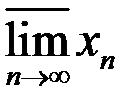 
, 
, 
, 
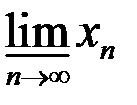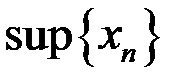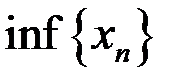для последовательностей: а)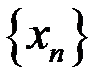 
;
б)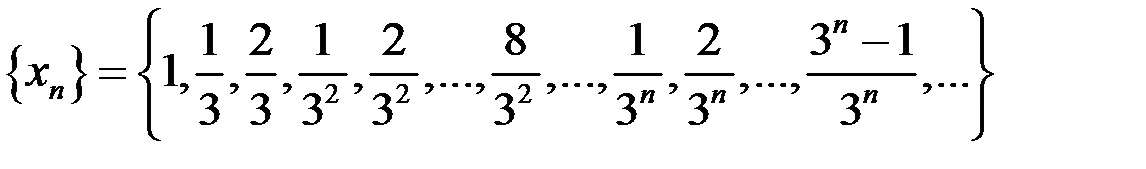 
.
8. Найти множество частичных пределов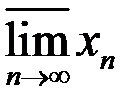 
, 
, 
, 
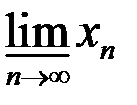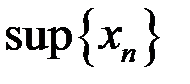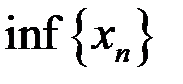для последовательностей: а)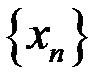 
;
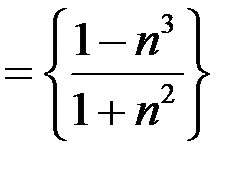б)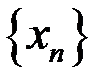 
= 
.
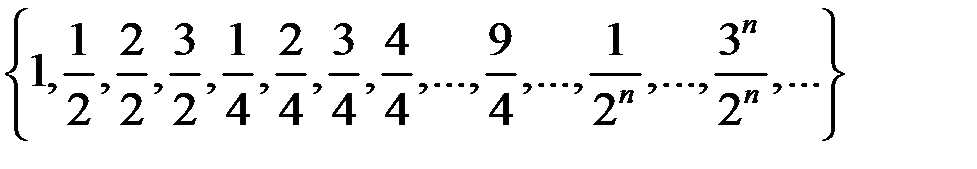9. Найти множество частичных пределов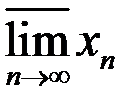 
, 
, 
, 
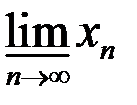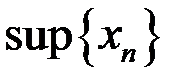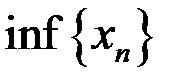для последовательностей: а)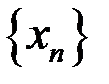 
;
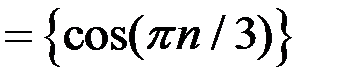б)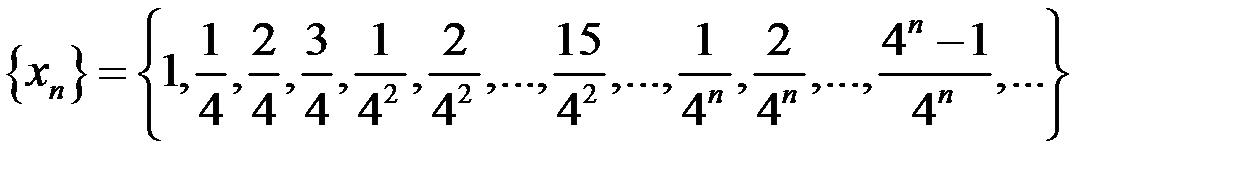 
.
10. Найти множество частичных пределов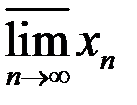 
, 
, 
, 
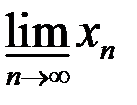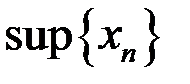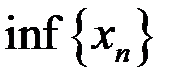для последовательностей: а) 
;
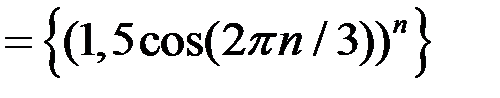б)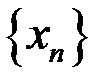 
= 
.
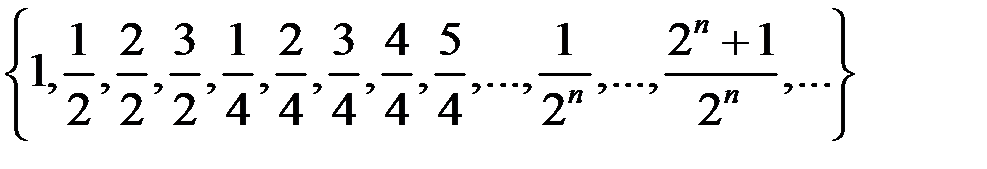Задание 5
1. Найти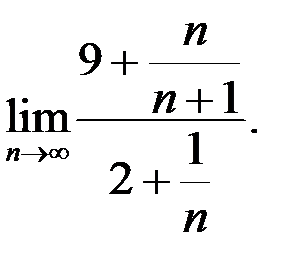 
2. Найти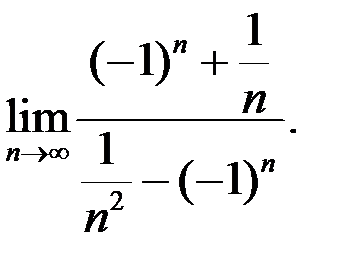 
3. Найти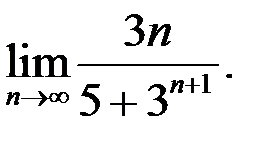 
4. Найти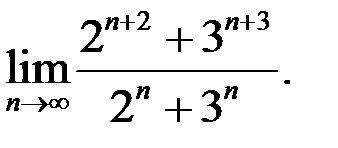 
5. Найти 
6. Найти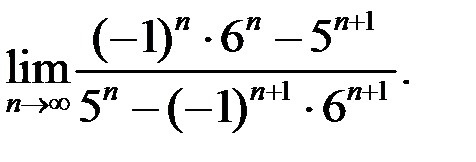 
7. Найти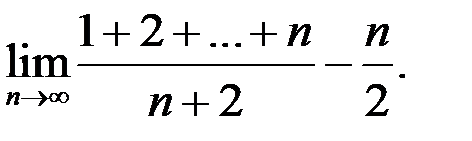 
8. Найти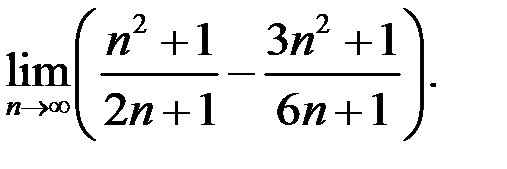 
9. Найти 
10. Найти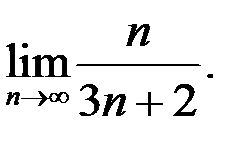 
Задание 6
1. Найти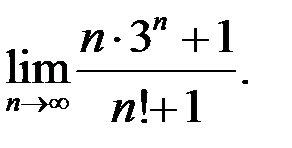 
2. Найти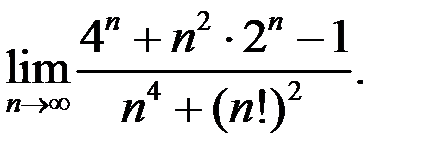 
3. Найти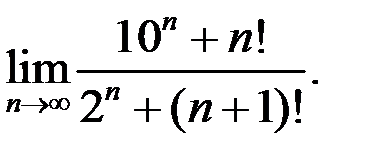 
4. Найти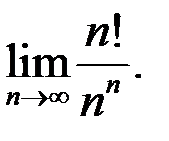 
5. Найти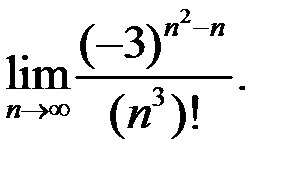 
6. Найти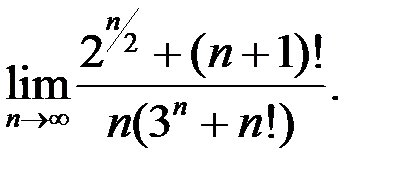 
7. Найти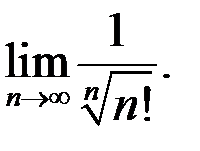 
8. Найти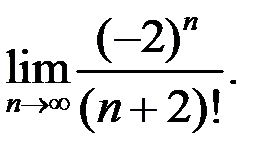 
9. Найти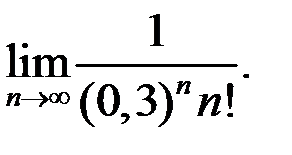 
10. Найти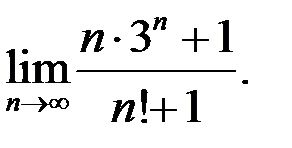 
Задание 7
1. Найти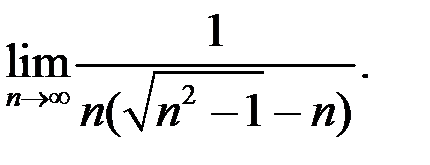 
2. Найти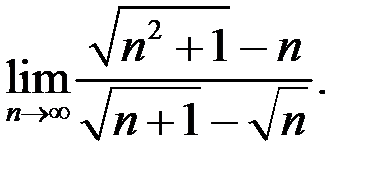 
3. Найти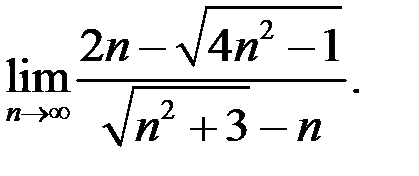 
4. Найти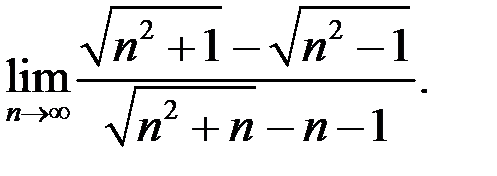 
5. Найти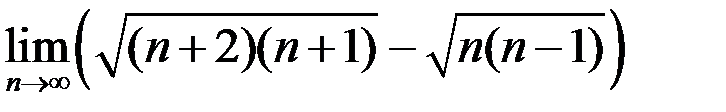 
.
6. Найти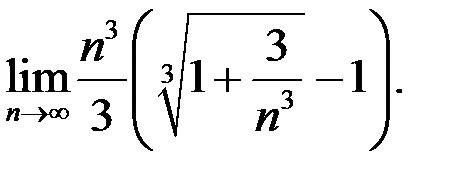 
7. Найти 
8. Найти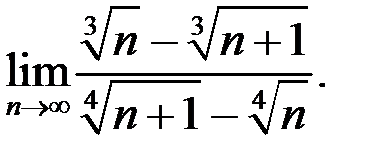 
9. Найти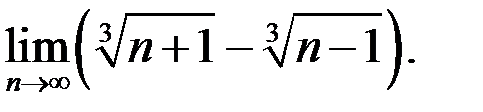 
10. Найти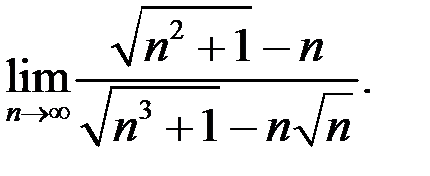 
Задание 8
1. Найти 
2. Найти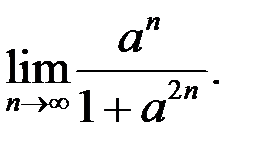 
3. Найти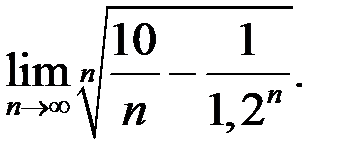 
4. Найти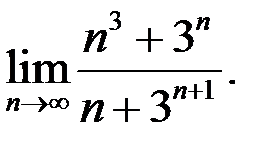 
5. Найти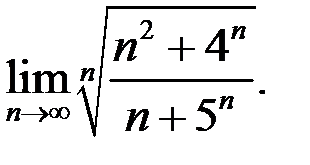 
6. Найти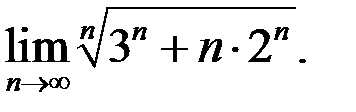 
7. Найти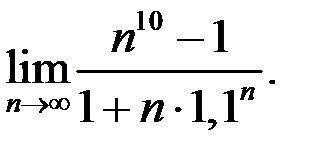 
8. Найти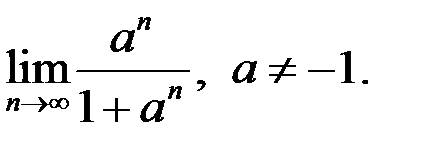 
9. Найти 
10. Найти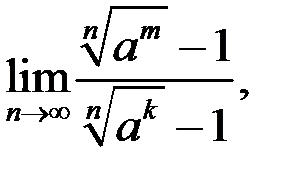 
.
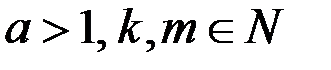Задание 9
1. Найти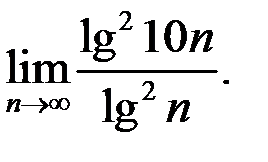 
2. Найти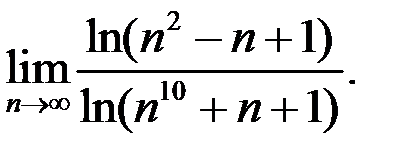 
3. Найти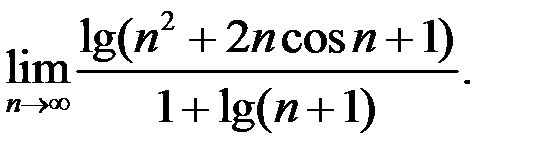 
4. Найти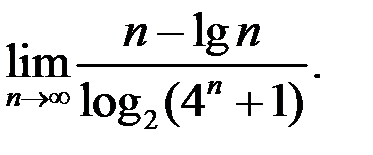 
5. Найти 
6. Найти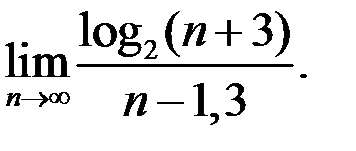 
7. Найти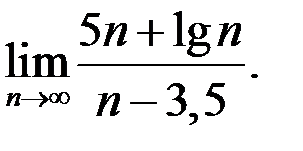 
8. Найти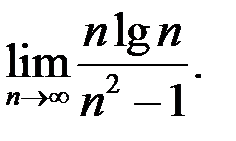 
9. Найти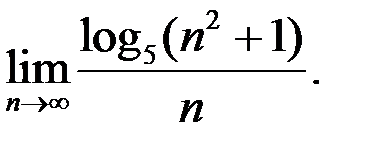 
10. Найти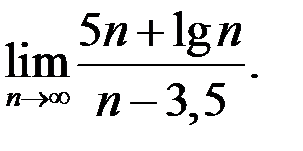 
Задание 10
1. Пользуясь определением, доказать: 
.
2. Пользуясь определением, доказать: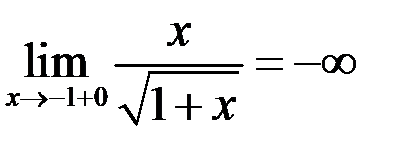 
.
3. Пользуясь определением, доказать: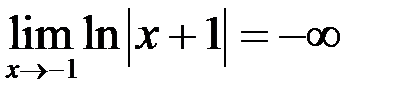 
.
4. Пользуясь определением, доказать: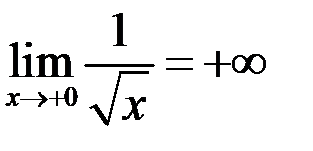 
.
5. Пользуясь определением, доказать: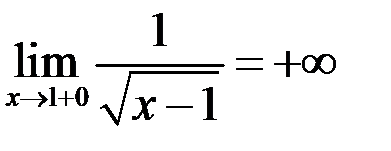 
.
6. Пользуясь определением, доказать: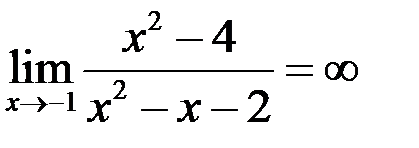 
.
7. Пользуясь определением, доказать: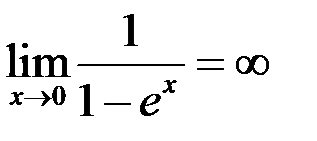 
.
8. Пользуясь определением, доказать: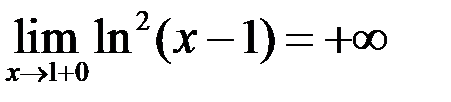 
.
9. Пользуясь определением, доказать: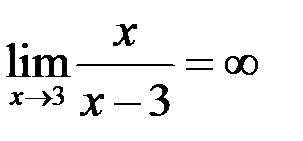 
.
10. Пользуясь определением, доказать: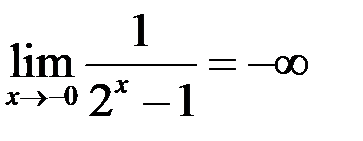 
.
Задание 11
1. Найти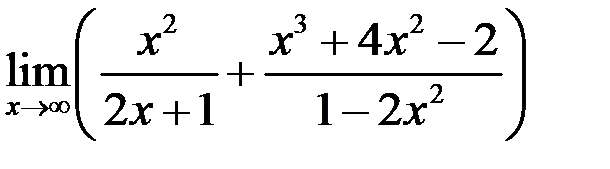 
.
2. Найти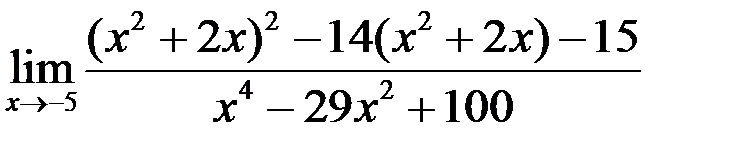 
.
3. Найти 
.
4. Найти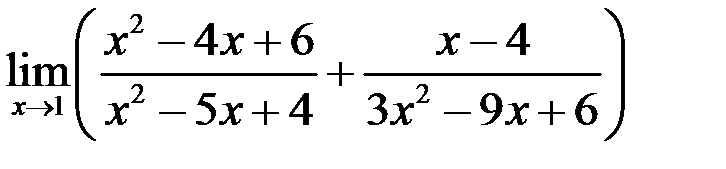 
.
5. Найти 
.
6. Найти 
.
7. Найти 
.
8. Найти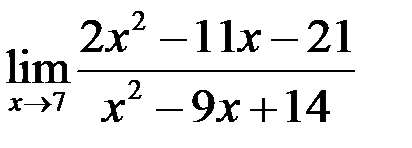 
.
9. Найти 
.
10. Найти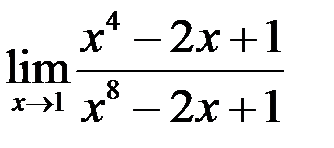 
.
Задание 12
1. Найти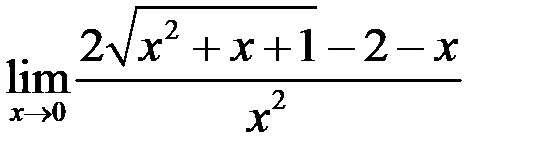 
.
2. Найти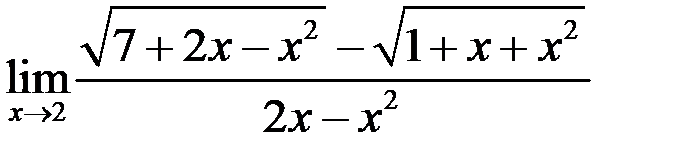 
.
3. Найти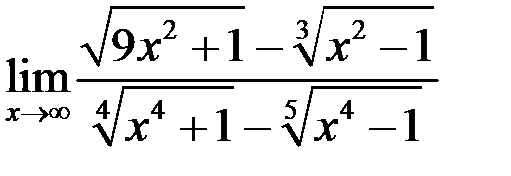 
.
4. Найти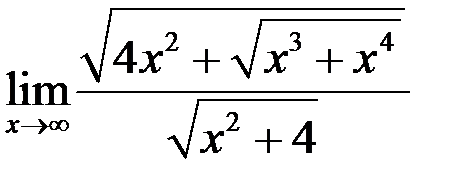 
.
5. Найти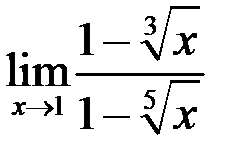 
.
6. Найти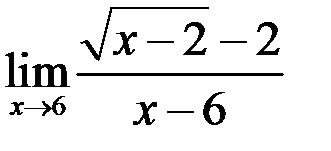 
.
7. Найти 
.
8. Найти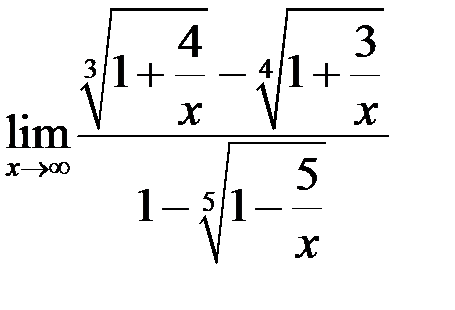 
.
9. Найти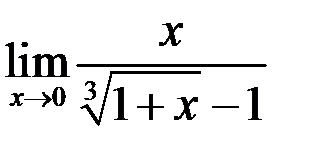 
.
10. Найти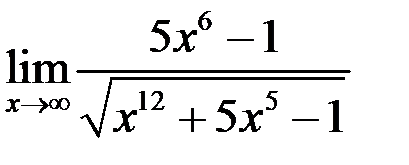 
.
Задание 13
1. Найти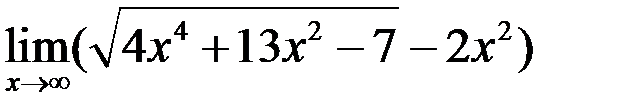 
.
2. Найти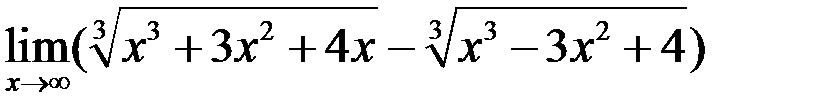 
.
3. Найти 
4. Найти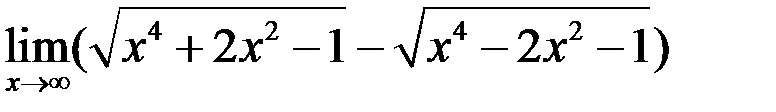 
.
5. Найти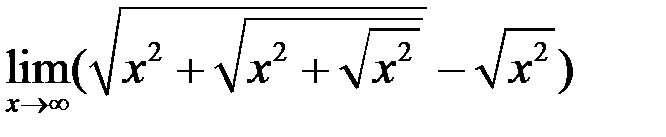 
.
6. Найти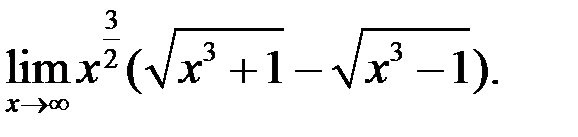 
7. Найти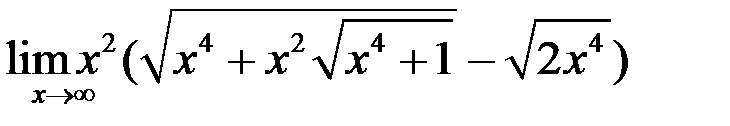 
.
8. Найти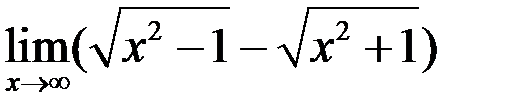 
.
9. Найти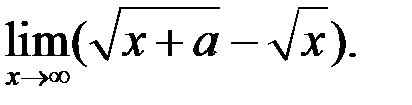 
10. Найти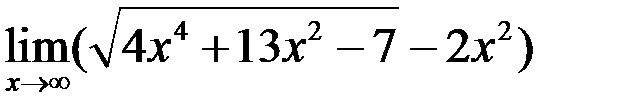 
.
Задание 14
1. Найти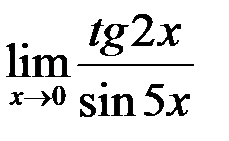 
.
2. Найти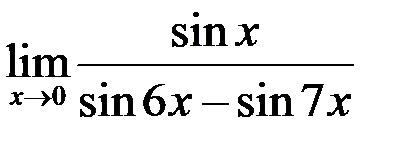 
.
3. Найти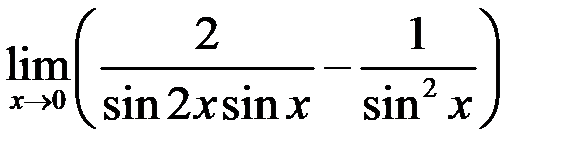 
.
4. Найти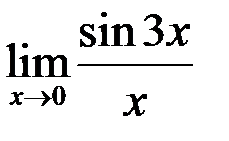 
.
5. Найти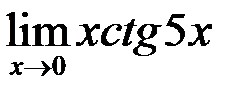 
.
6. Найти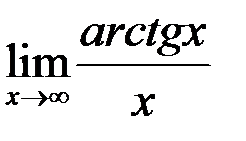 
.
7. Найти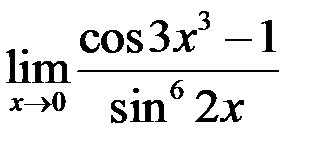 
.
8. Найти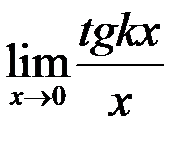 
.
9. Найти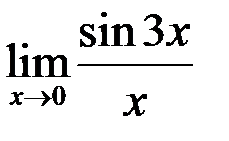 
.
10. Найти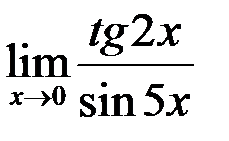 
.
Задание 15
1. Найти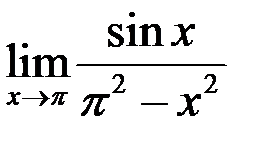 
.
2. Найти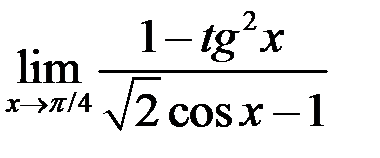 
.
3. Найти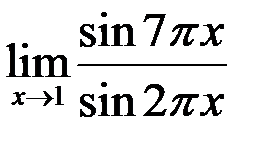 
.
4. Найти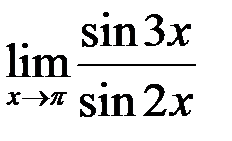 
.
5. Найти 
.
6. Найти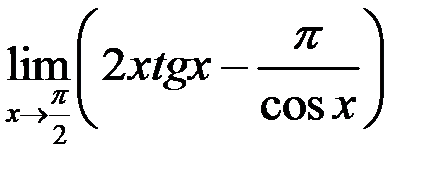 
.
7. Найти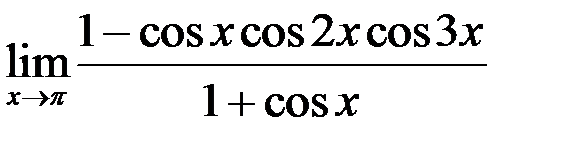 
.
8. Найти 
.
9. Найти 
.
10. Найти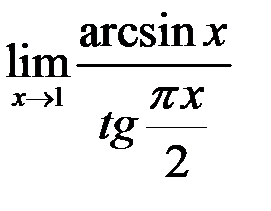 
.
Задание 16
1. Найти 
.
2. Найти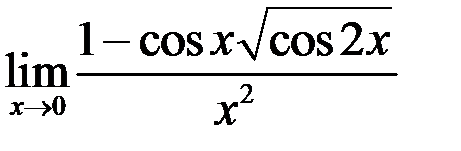 
.
3. Найти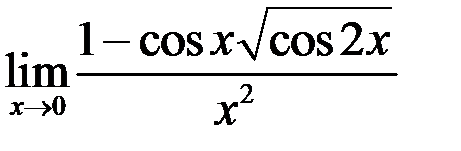 
.
4. Найти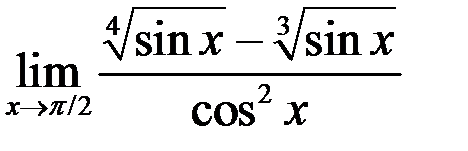 
.
5. Найти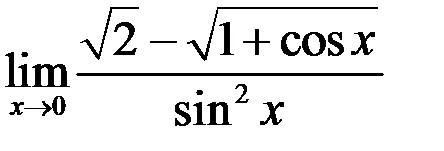 
.
6. Найти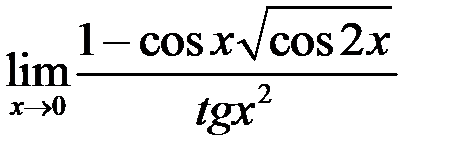 
.
7. Найти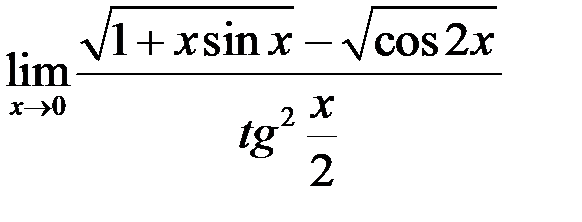 
.
8. Найти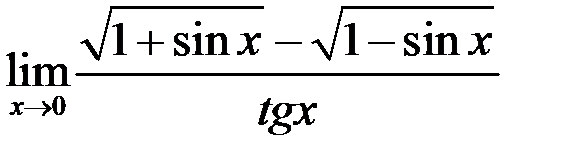 
.
9. Найти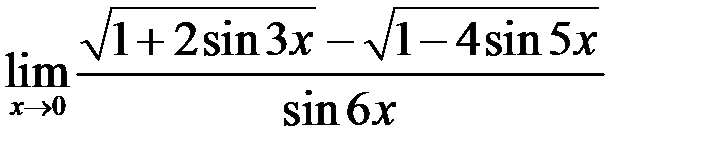 
.
10. Найти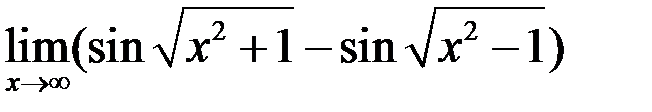 
.
Задание 17
1. Найти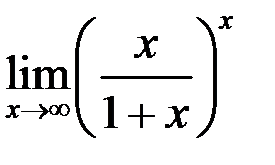 
.
2. Найти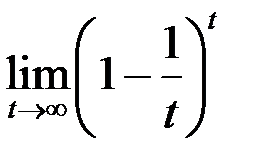 
.
3. Найти 
.
4. Найти 
.
5. Найти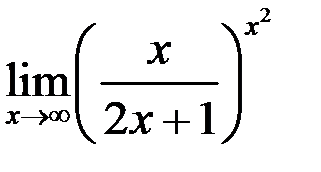 
.
6. Найти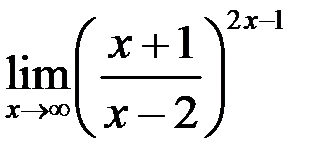 
.
7. Найти 
.
8. Найти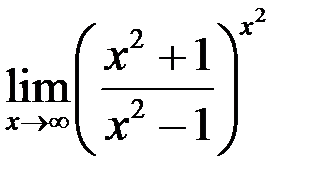 
.
9. Найти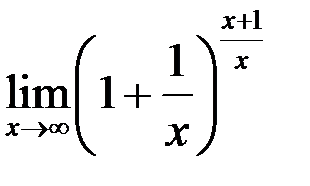 
.
10. Найти 
.
Задание 18
1. Найти 
.
2. Найти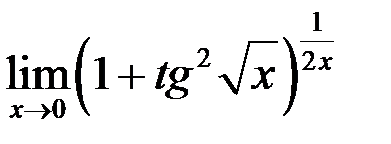 
.
3. Найти 
.
4. Найти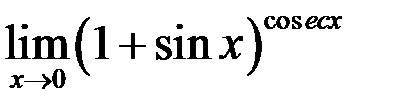 
.
5. Найти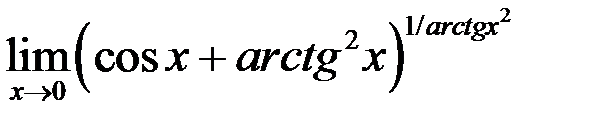 
.
6. Найти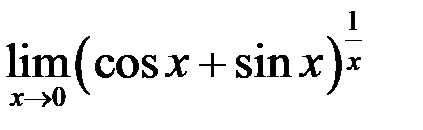 
.
7. Найти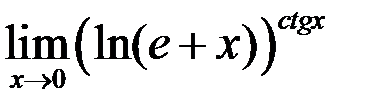 
.
8. Найти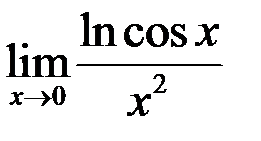 
.
9. Найти: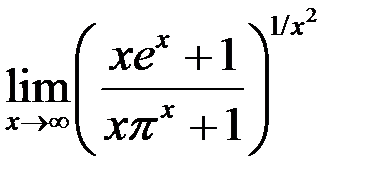 
.
10. Найти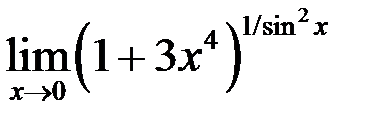 
.
Задание 19
1. Найти: а)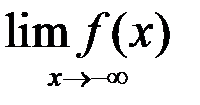 
; б)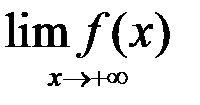 
: 
.
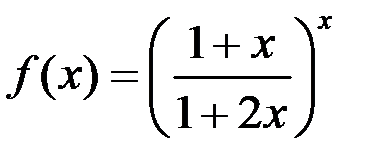2. Найти: а) 
; б) 
: 
.
3. Найти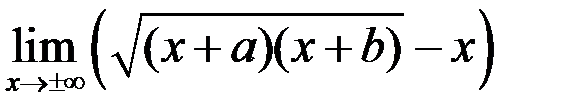 
.
4. Найти: а)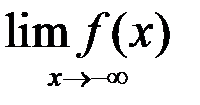 
; б)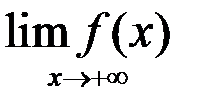 
: 
.
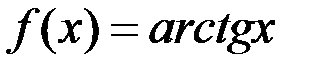5. Найти: а)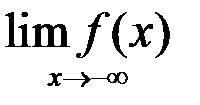 
; б)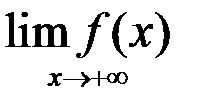 
: 
.
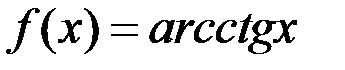6. Найти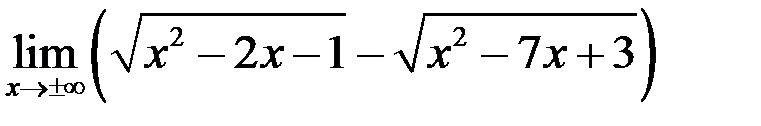 
.
7. Найти: а)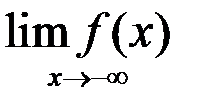 
; б) 
: 
.
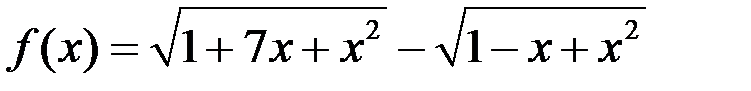8. Найти: а)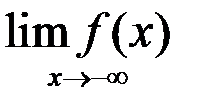 
; б)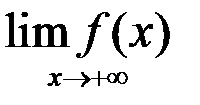 
: 
.
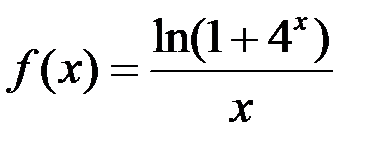9. Найти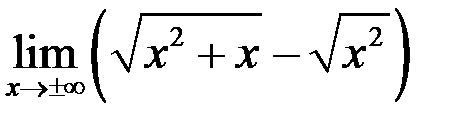 
.
10. Найти: а) 
; б) 
: 
.
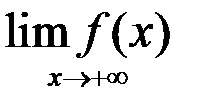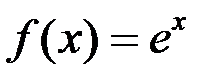Задание 20
1. Найти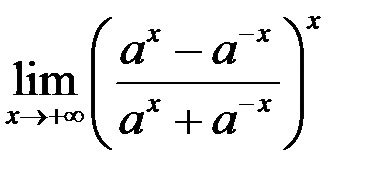 
, a >0.
2. Найти: 
.
3. Найти: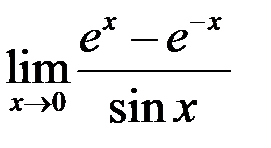 
.
4. Найти: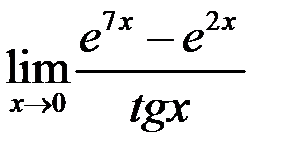 
.
5. Найти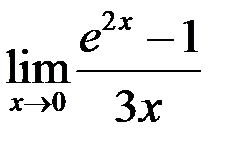 
.
6. Найти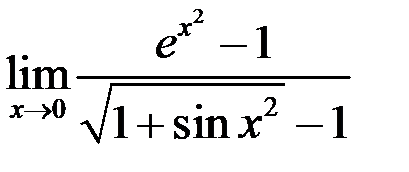 
.
7. Найти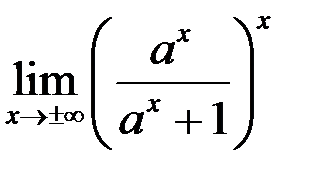 
, a >0.
8. Найти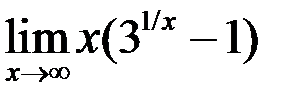 
.
9. Найти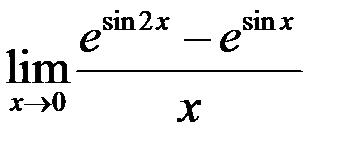 
.
10. Найти 
.
Задание 21
1. Найти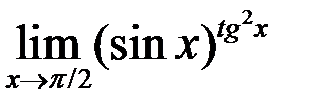 
.
2. Найти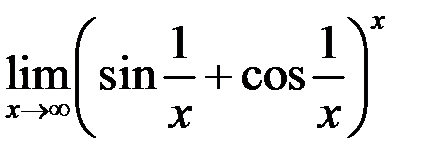 
.
3. Найти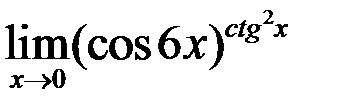 
.
4. Найти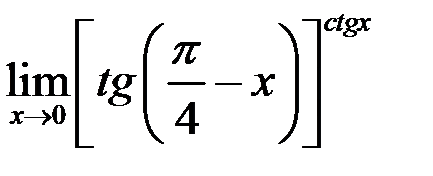 
.
5. Найти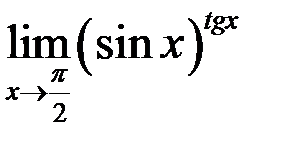 
.
6. Найти 
.
7. Найти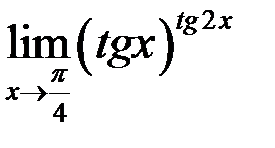 
.
8. Найти 
.
9. Найти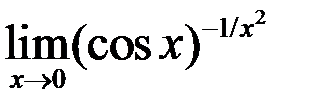 
.
10. Найти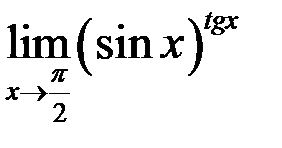 
.
Задание 22
1. Найти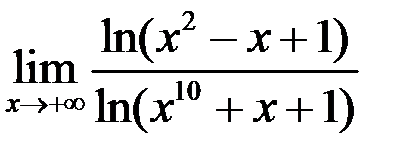 
.
2. Найти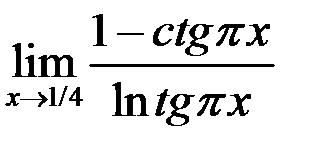 
.
3. Найти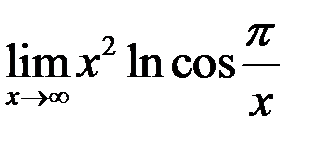 
.
4. Найти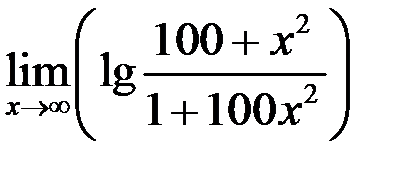 
.
5. Найти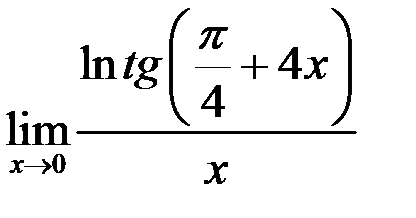 
.
6. Найти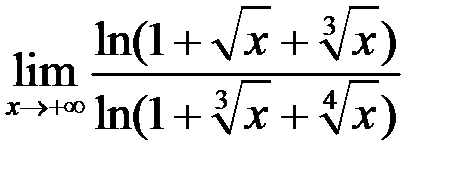 
.
7. Найти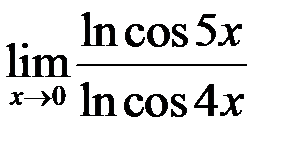 
.
8. Найти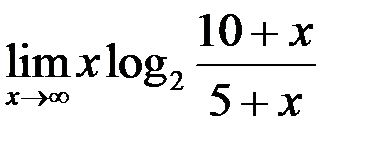 
.
9. Найти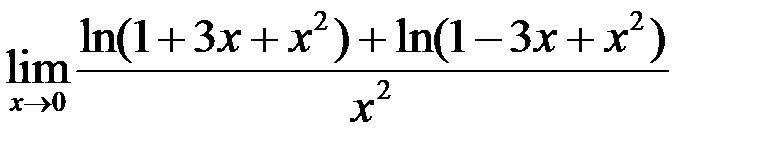 
.
10. Найти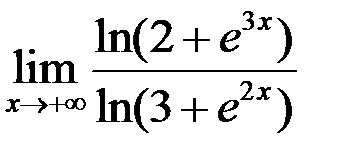 
Задание 23
1. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: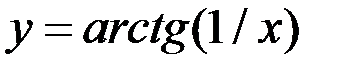 
.
2. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: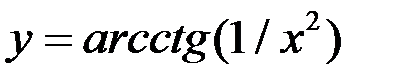 
.
3. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: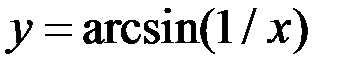 
.
4. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: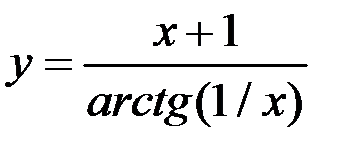 
.
5. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: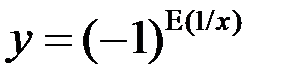 
.
6. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: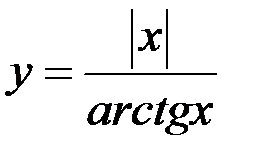 
.
7. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: 
.
8. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: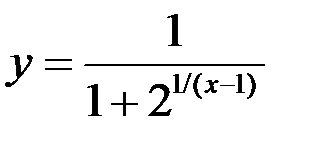 
.
9. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: 
.
10. Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода: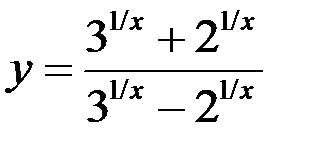 
.
Задание 24
1. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: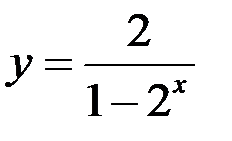 
.
2. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: 
.
3. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: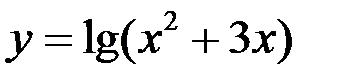 
.
4. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: 
.
5. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: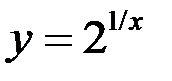 
.
6. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: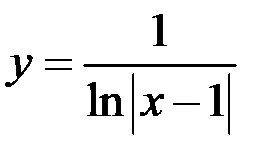 
.
7. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: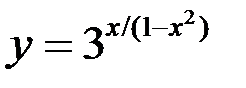 
.
8. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: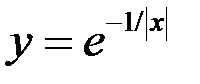 
.
9. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: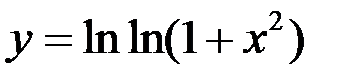 
.
10. Найдите точки разрыва функции, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва: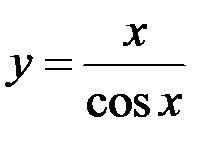 
.
Задание 25
1. При каком значении а функция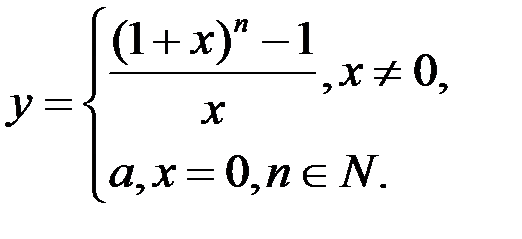 
будет непрерывна?
2. При каком значении а функция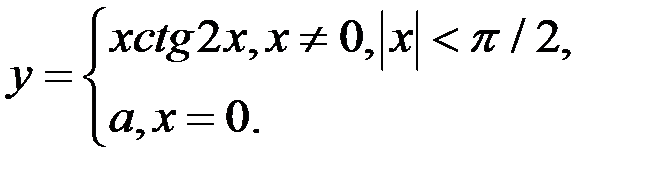 
будет непрерывна?
3. При каком значении а функция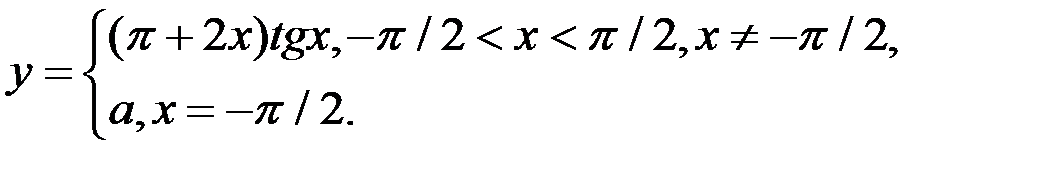 
будет непрерывна?
4. При каком значении а функция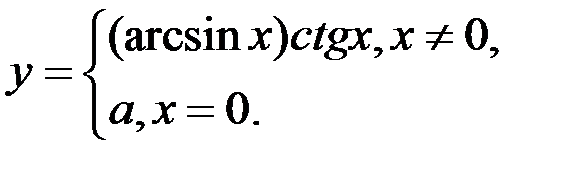 
будет непрерывна?
5. При каком значении а функция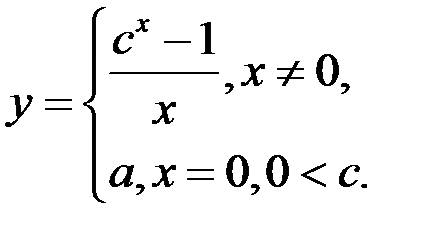 
будет непрерывна?
6. При каком значении а функция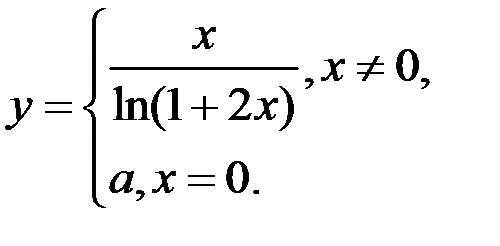 
будет непрерывна?
7. При каком значении а функция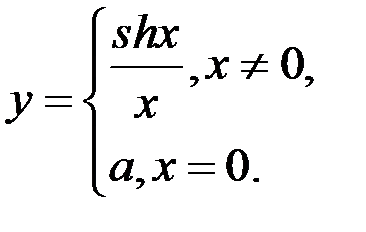 
будет непрерывна?
8. При каком значении а функция 
будет непрерывна?
9. При каком значении а функция 
будет непрерывна?
10. При каком значении а функция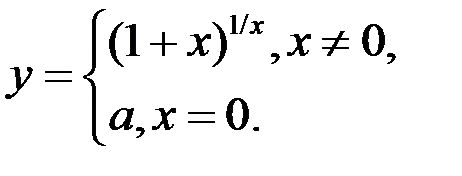 
будет непрерывна?
Задание 26
1. Найдите точки разрыва функции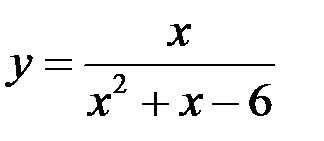 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
2. Найдите точки разрыва функции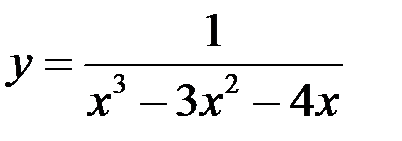 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
3. Найдите точки разрыва функции 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
4. Найдите точки разрыва функции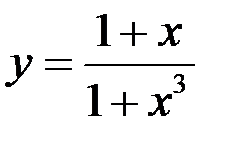 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
5. Найдите точки разрыва функции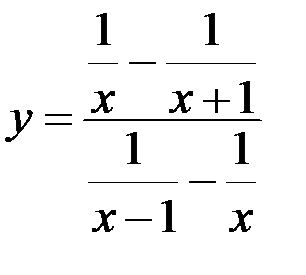 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
6. Найдите точки разрыва функции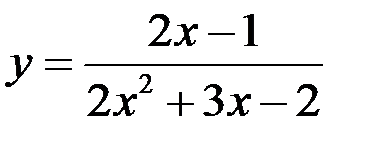 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
7. Найдите точки разрыва функции 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
8. Найдите точки разрыва функции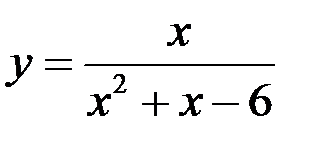 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
9. Найдите точки разрыва функции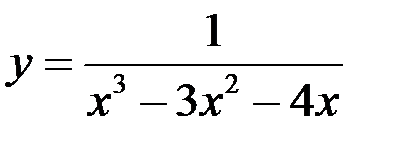 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
10. Найдите точки разрыва функции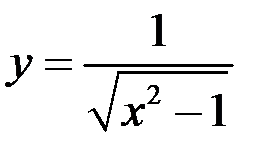 
, установите их род, доопределите функцию по непрерывности в точках устранимого разрыва:
Задание 27
1. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:
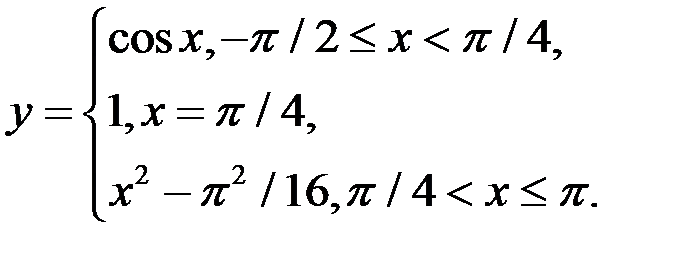
2. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:
3. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:
4. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:
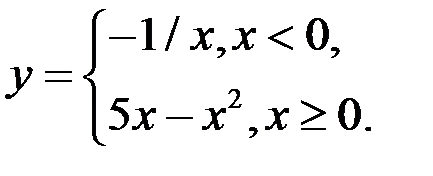
5. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:
6. Можно ли доопределить функцию в точке разрыва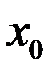 
так, чтобы она стала непрерывной в этой точке: 
.
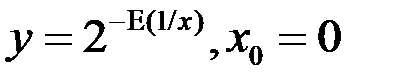7. Можно ли доопределить функцию в точке разрыва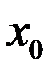 
так, чтобы она стала непрерывной в этой точке: 
.
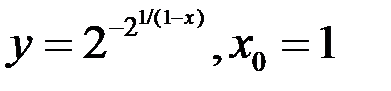8. Можно ли доопределить функцию в точке разрыва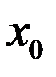 
так, чтобы она стала непрерывной в этой точке: 
.
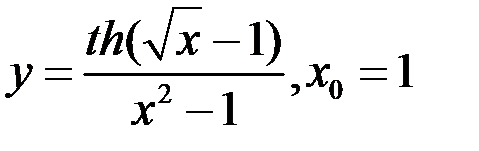9. Можно ли доопределить функцию в точке разрыва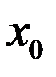 
так, чтобы она стала непрерывной в этой точке: 
.
10. Можно ли доопределить функцию в точке разрыва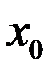 
так, чтобы она стала непрерывной в этой точке: 
.
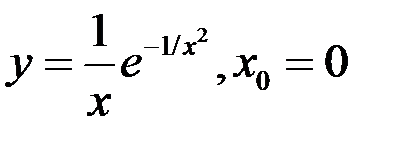Задание 28
1. Исследовать функцию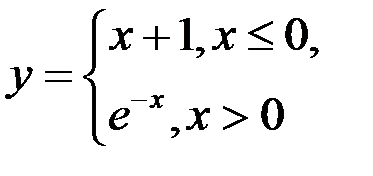 
на равномерную непрерывность на множестве 
.
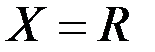2. Исследовать функцию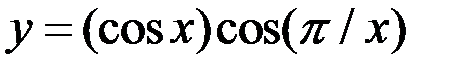 
на равномерную непрерывность на множестве 
.
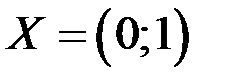3. Исследовать функцию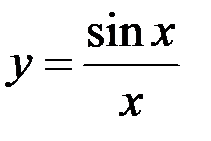 
на равномерную непрерывность на множестве 
.
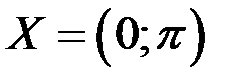4. Исследовать функцию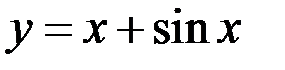 
на равномерную непрерывность на множестве 
.
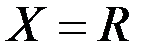5. Исследовать функцию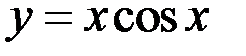 
на равномерную непрерывность на множестве 
.
6. Исследовать функцию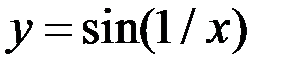 
на равномерную непрерывность на множестве 
.
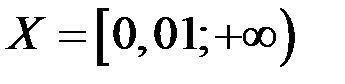7. Исследовать функцию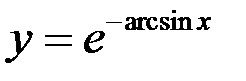 
на равномерную непрерывность на множестве 
.
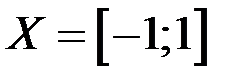8. Исследовать функцию 
на равномерную непрерывность на множестве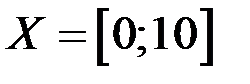 
.
9. Исследовать функцию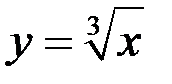 
на равномерную непрерывность на множестве 
.
10. Исследовать функцию 
на равномерную непрерывность на множестве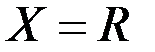 
.
Задание 29
1. Исследовать на равномерную непрерывность в заданной области функцию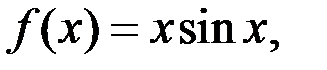 
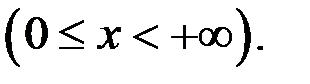
2. Исследовать на равномерную непрерывность в заданной области функцию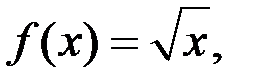 
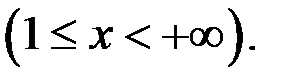
3. Исследовать на равномерную непрерывность в заданной области функцию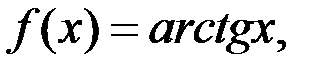 
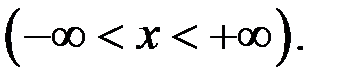
4. Исследовать на равномерную непрерывность в заданной области функцию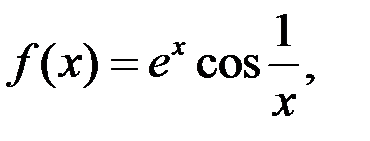 
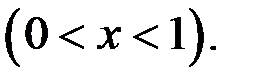
5. Исследовать на равномерную непрерывность в заданной области функцию 
6. Исследовать на равномерную непрерывность в заданной области функцию 
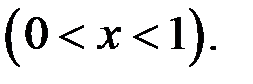
7. Исследовать на равномерную непрерывность в заданной области функцию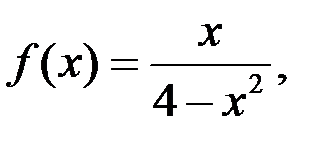 
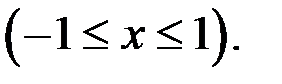
8. Исследовать на равномерную непрерывность в заданной области функцию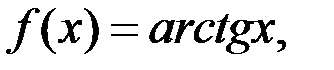 
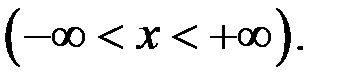
9. Исследовать на равномерную непрерывность в заданной области функцию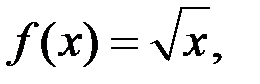 
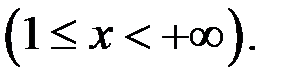
10. Исследовать на равномерную непрерывность в заданной области функцию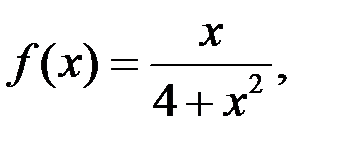 
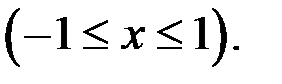
Варианты индивидуального задания «Производная»
Задание 1. Найти производные функций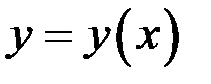 
, заданных явно; неявно; параметрически
1) 
; 
; 
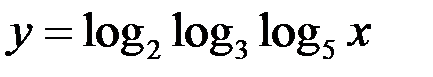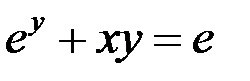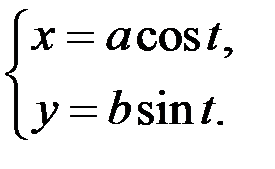
2) 
; 
; 
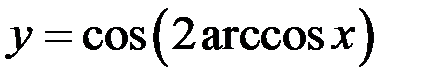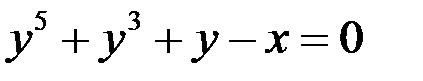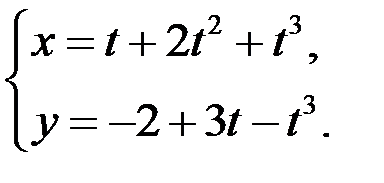
3) 
; 
; 
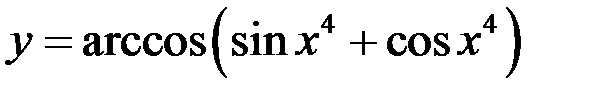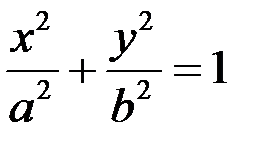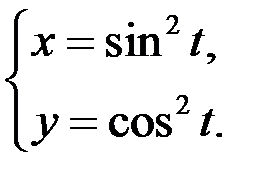
4) 
; 
; 
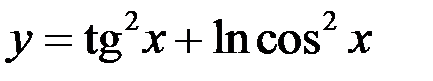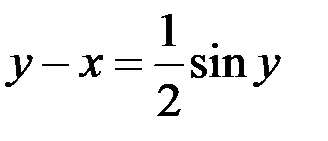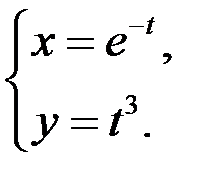
5) 
; 
; 
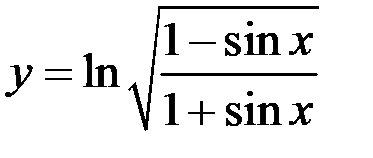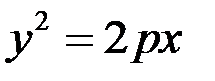6) 
; 
; 
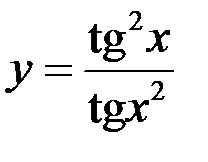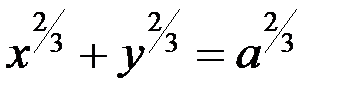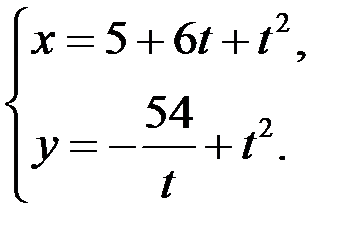
7) 
; 
; 
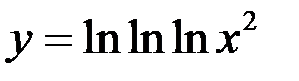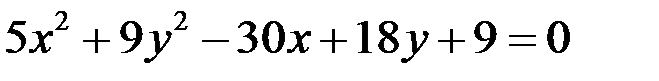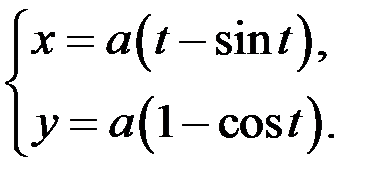
8) 
; 
; 
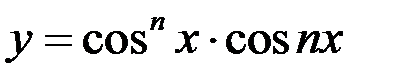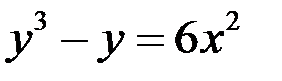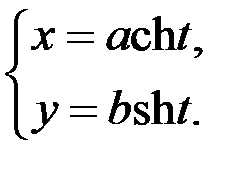
9) 
; 
; 
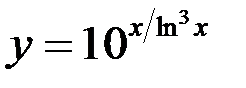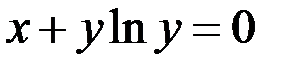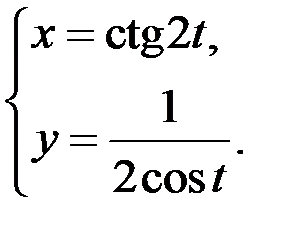
10) 
; 
; 
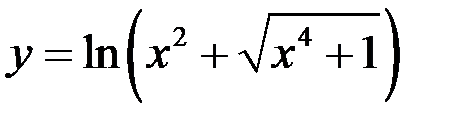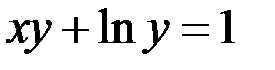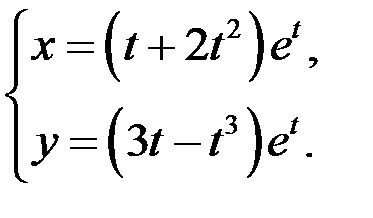
Задание 2.
Определить значения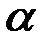 
и β, при которых функция а) всюду непрерывна, б) всюду дифференцируема:
1) 
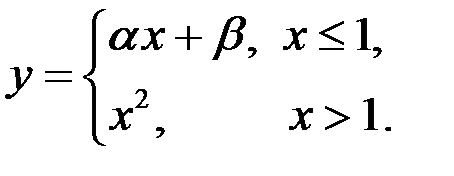
2) 
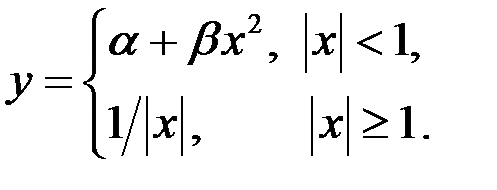
3) 
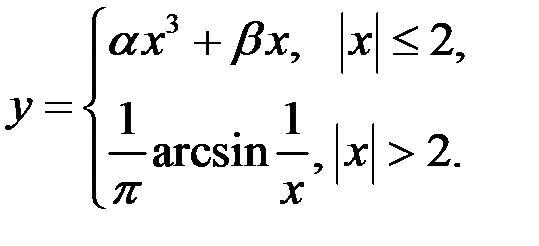
4) 
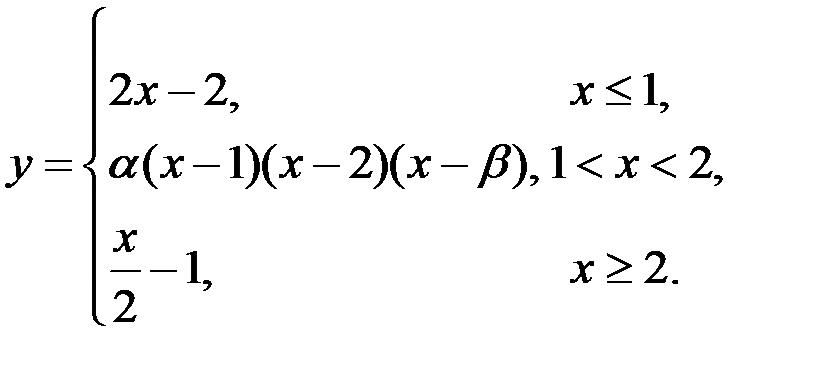
5) 
Исследовать функцию на дифференцируемость:
6) 
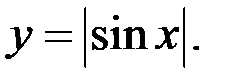
7) 
8) 
9) 
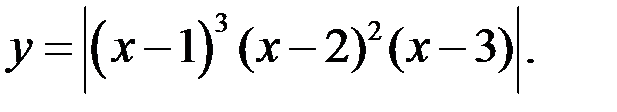
10) 
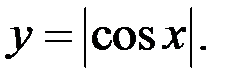
Задание 3. Написать уравнение касательной и нормали к кривой в точке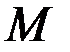 
.
1) 
;
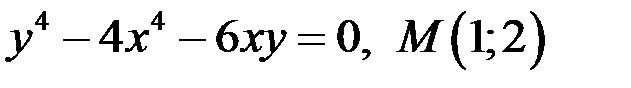2) 
;
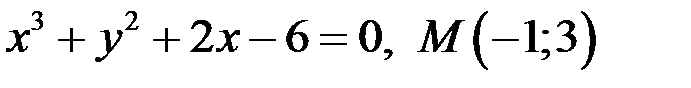3) 
;
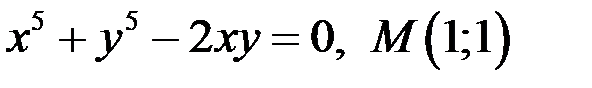4) 
;
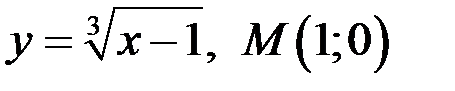5) 
;
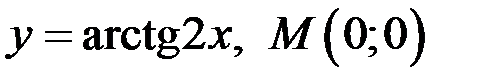6) 
;
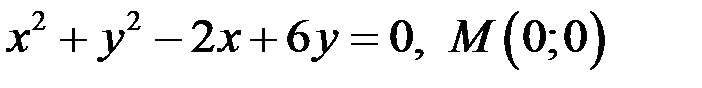7) 
;
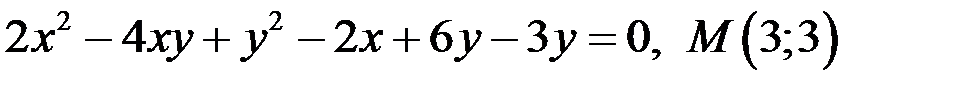8) 
;
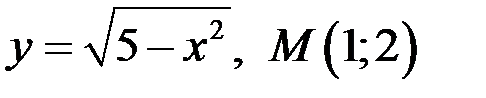9) 
;
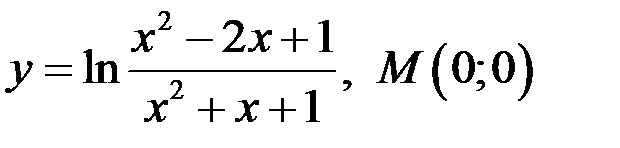10) 
;
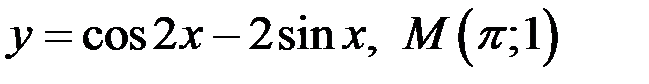Задание 4. Найти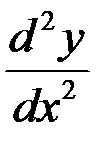 
для функций, заданных явно; параметрически:
1) 
; 
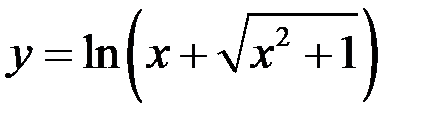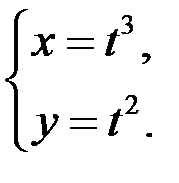
2) 
; 
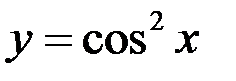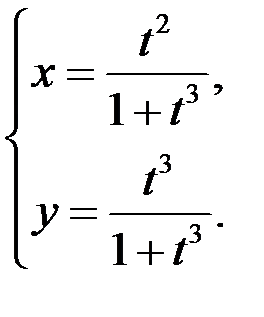
3) 
; 
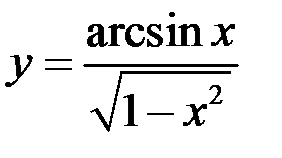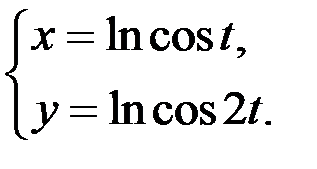
4) 
; 
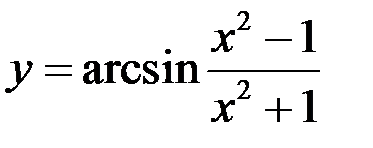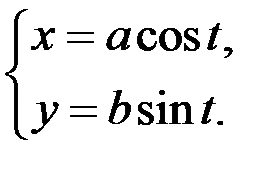
5) 
; 
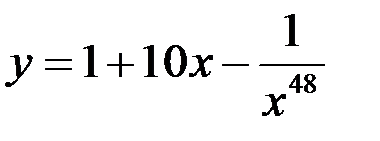6) 
; 
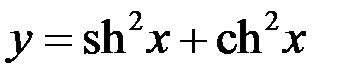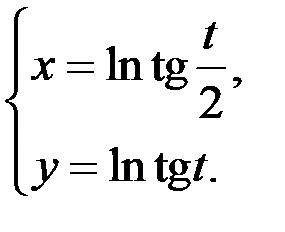
7) 
; 
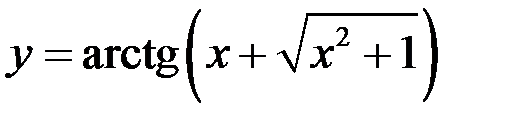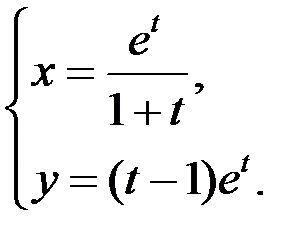
8) 
; 
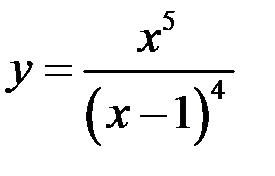9) 
; 
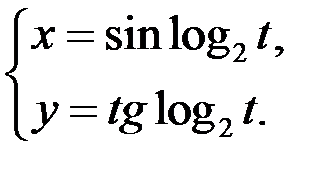
10) 
; 
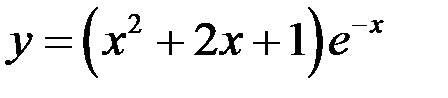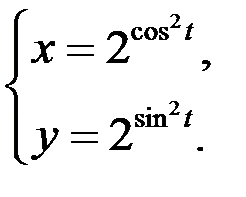
Примеры решения задач
1. Доказать, что последовательность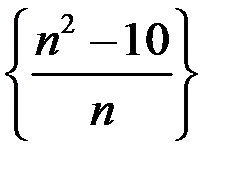 
расходится.
Решение. Докажем, что данная последовательность неограниченна. Так как в формуле общего члена последовательности степень числителя (2) больше степени знаменателя (1), то наша задача заключается в том, чтобы равносильными переходами (равенством =) или оценками снизу (неравенством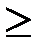 
) упростить выражение, сохранив лишнее 
в числителе. Например, уменьшив числитель, а затем, увеличив знаменатель, имеем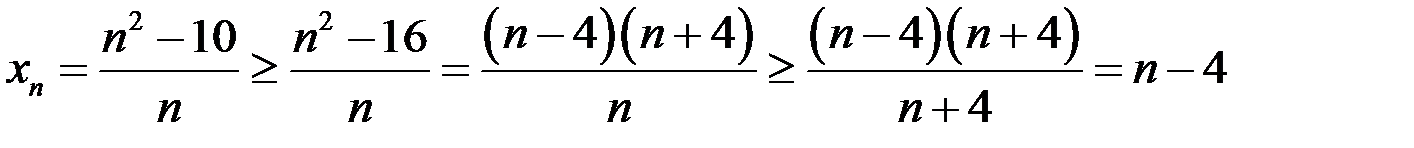 
.
Получили оценку снизу: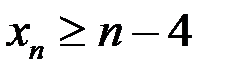 
. Последовательность неограниченна, если для любой константы 
найдется элемент 
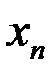такой, что 
.
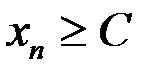Пусть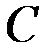 
– произвольное положительное число. Возьмем какое-нибудь натуральное число 
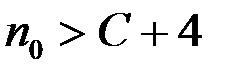, тогда 
.
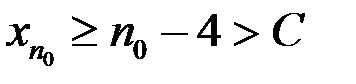Это означает, что последовательность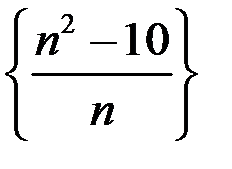 
неограниченна, не имеет конечного предела, а поэтому расходится.
2. Доказать по определению предела, что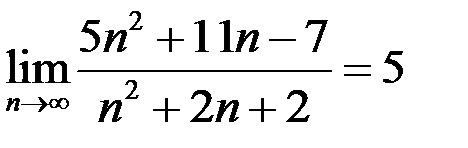 
.
Решение. Запишем определение предела на языке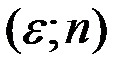 
:
.
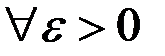
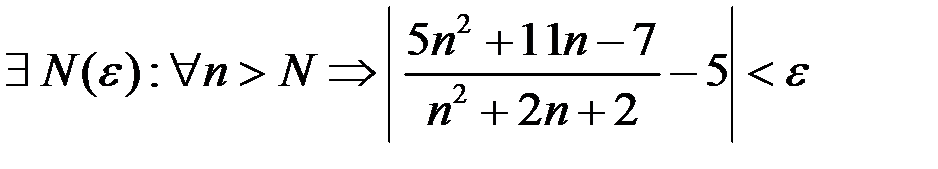Зафиксируем некоторое произвольное положительное 
и будем искать 
.
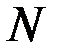Неравенство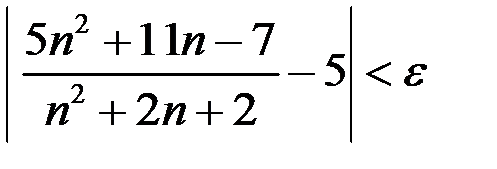 
эквивалентными преобразованиями приведем к виду 
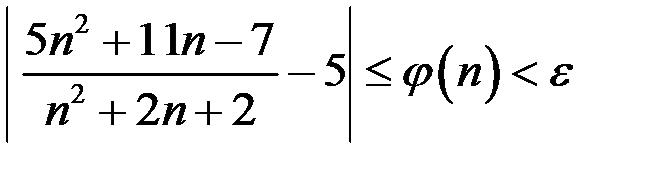, с целью получения неравенства 
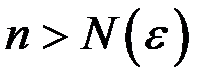. При этом наша цель – получить как можно более простой вид 
.
Приводим к общему знаменателю и упрощаем выражение в числителе:
.
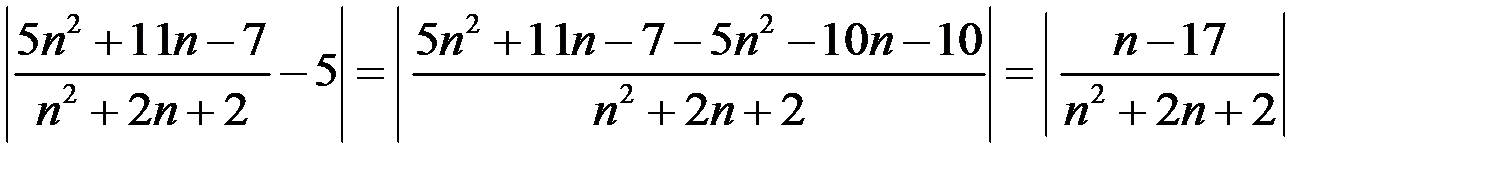В связи с тем, что мы исследуем наше выражение при больших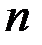 
(т. к. 
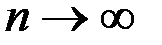), то чтобы избавиться от модуля, учтем знак при коэффициенте старшей степени.
.
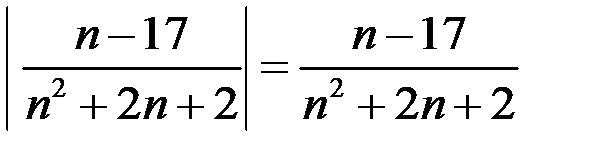Заметим, что это справедливо при 
.
Контрольный момент. Наибольшая степень 
в знаменателе больше степени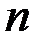 
в числителе.
Упростим дробь (выражение можно увеличивать), обязательно оставив лишнее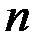 
в знаменателе.
Чтобы добиться цели, необходимо оставить только главные (старшие) слагаемые и в числителе, и в знаменателе. Следовательно, желательно в числителе отбросить (–17), а в знаменателе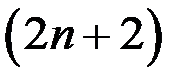 
. Можно ли избавиться в числителе от (–17)? Да, ведь при этом наша дробь увеличится. Следовательно,
.
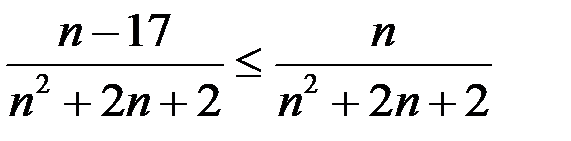Аналогично, отбросив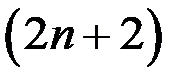 
в знаменателе, мы его уменьшим, а дробь увеличим:
.
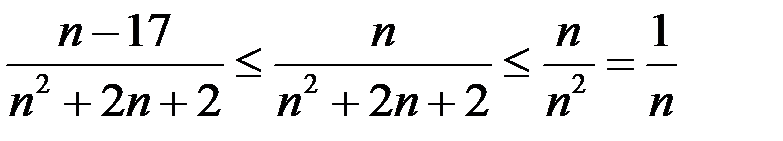В результате сделанных преобразований получено упрощенное выражение вида 
.
Следовательно, искомый номер равен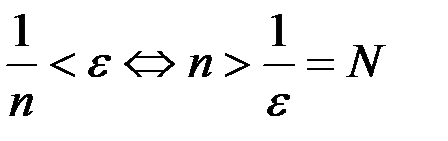 
.
Мы должны учесть ограничения на 
, возникшие в процессе решения 
, а также то, что полученная дробь может оказаться не целым числом. С учетом указанного искомый номер равен
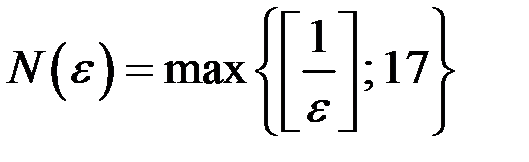
Нам удалось по фиксированному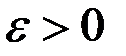 
найти номер 
, а значит доказать утверждение задачи.
3. Доказать, что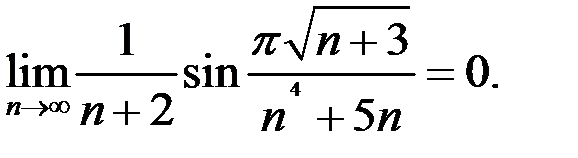 
Решение. Рассмотрим последовательность 
. Данная последовательность является ограниченной, так как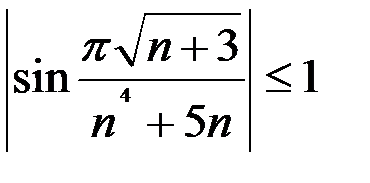 
.
Возьмем последовательность с общим членом 
, она является бесконечно малой последовательностью, так как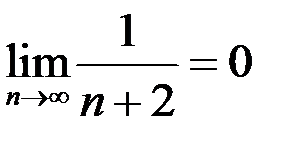 
.
По свойству 3 бесконечно малых последовательностей произведение ограниченной последовательности 
на бесконечно малую последовательность 
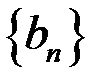есть бесконечно малая последовательность. Данная последовательность 
есть бесконечно малая последовательность, то есть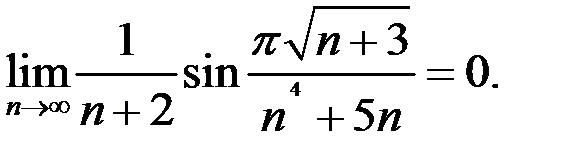 
4. Найти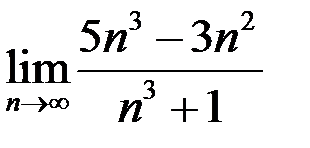 
.
Решение. Имеем неопределенность вида 
. Избавимся от неопределенности, разделив числитель и знаменатель на наибольшую степень 
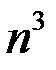. Получим
.
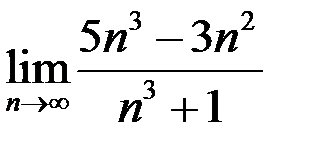
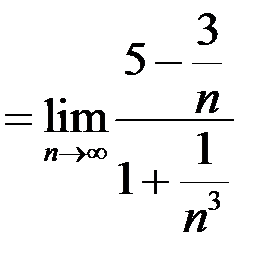От неопределенности избавились. Вычисляем предел. Учитывая, что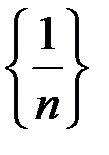 
и 
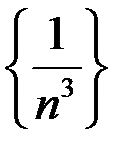– бесконечно малые последовательности, и используя теоремы об арифметических операциях над пределами, получаем:
.
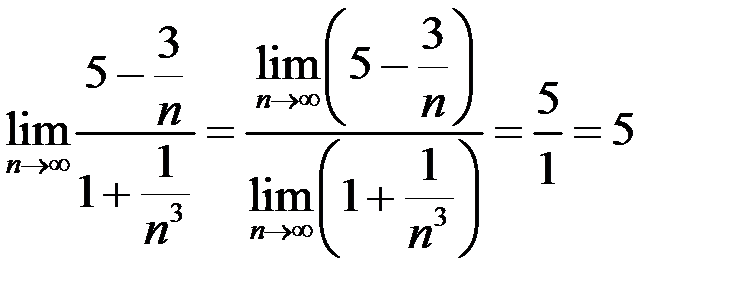5. Найти предел функции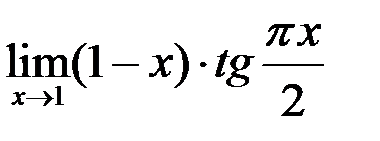 
.
Решение. Приведем неопределенность вида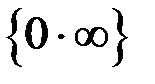 
к виду 
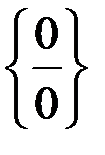под знаком предела.
Сделаем это с помощью подстановки 
.
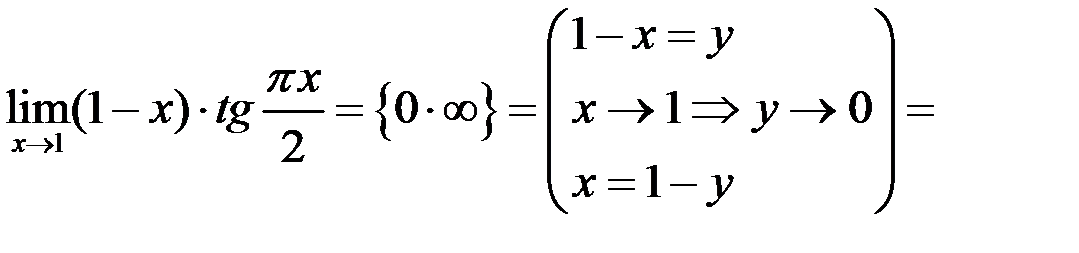
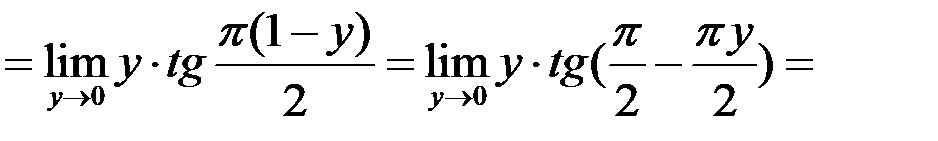
Избавимся от неопределенности, применив первый замечательный предел
.
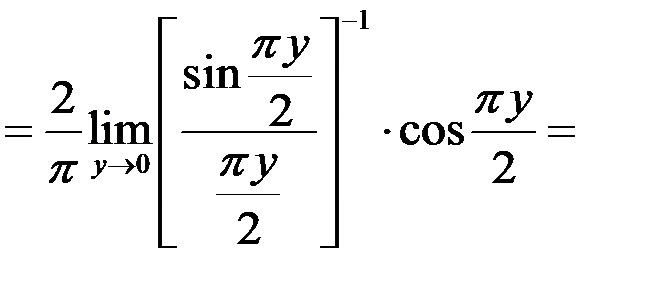
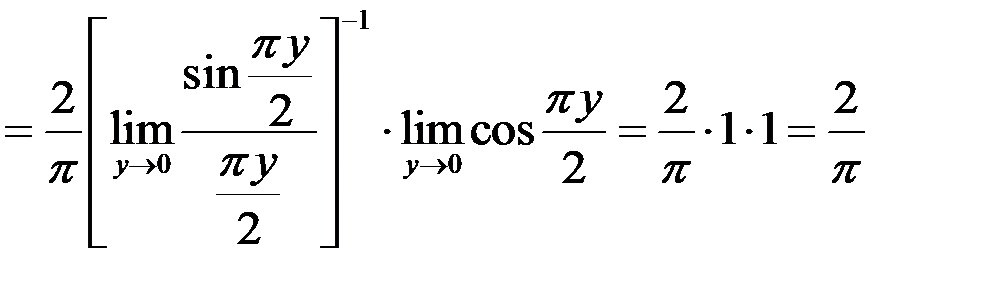Таким образом, получаем ответ: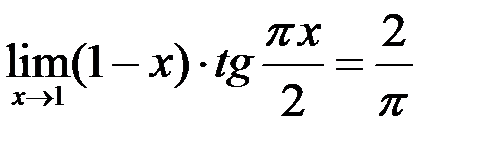 
.
6. Вычислить предел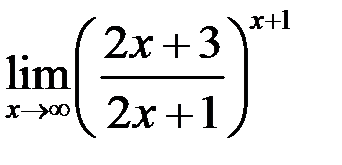 
.
Решение. Преобразуем неопределенность вида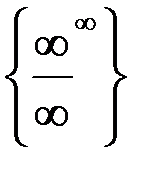 
к виду 
произведя замену:
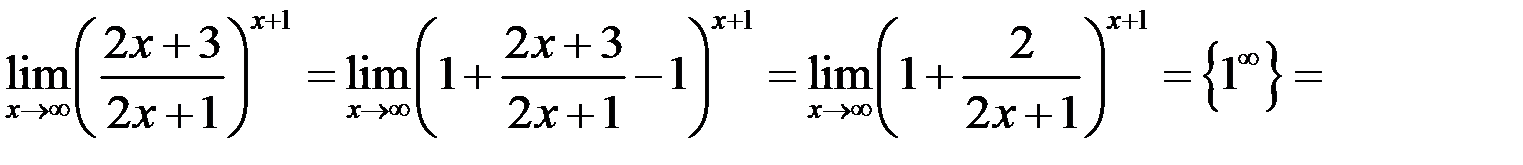
Избавимся от неопределенности, применив второй замечательный предел
.
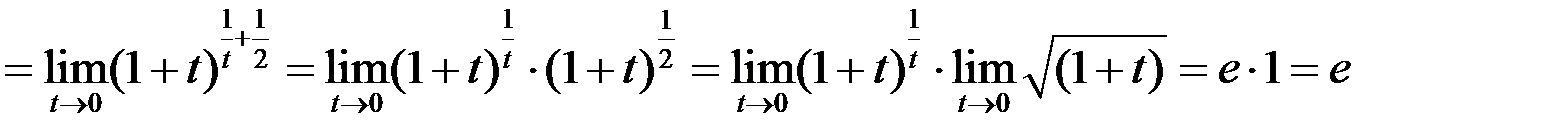Итак, получаем ответ: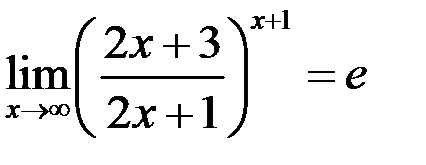 
.
7. Проверить, являются ли функци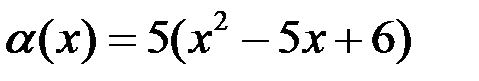и 
и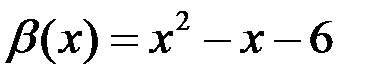 
эквивалентными бесконечно малыми при 
.
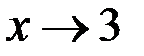Решение. Проверим вначале, что данные функции являются бесконечно малыми функциями в точке 
.
; 
.
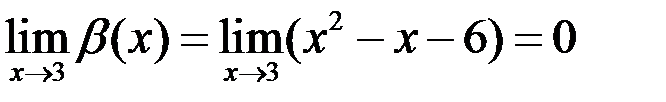Найдем предел отношения этих функций:
.
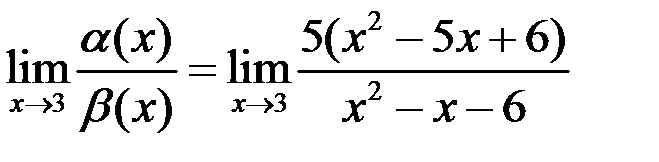Имеем неопределенность вида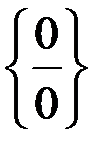 
. Выделим множители 
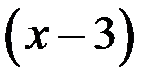, стремящиеся к нулю в числителе и знаменателе, и сократим на них
.
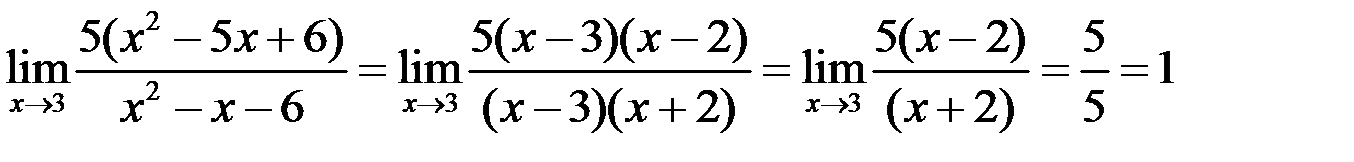Так как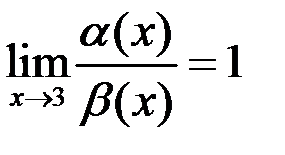 
, то, по определению, заданные функци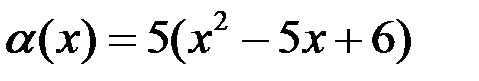и 
и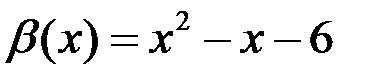 
являются эквивалентными бесконечно малыми.
8. Исследовать функцию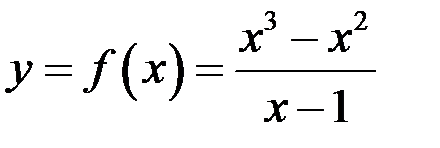 
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж графика функции.
Решение. Функция 
является элементарной на области определения. Из области определения выпадает единственная точка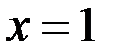 
, в которой функция не определена. В остальных точках числовой оси, то есть на интервалах 
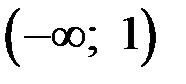и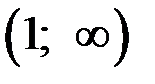 
, функция непрерывна, как элементарная. Точка 
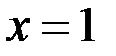является точкой, подозрительной на разрыв. Но так как эта точка не попадает в область определения, то функция в ней не определена. А раз не существует значения функции в этой точке, то это обязательно точка разрыва.
Определим, какого рода разрыв. Вычислим односторонние пределы:
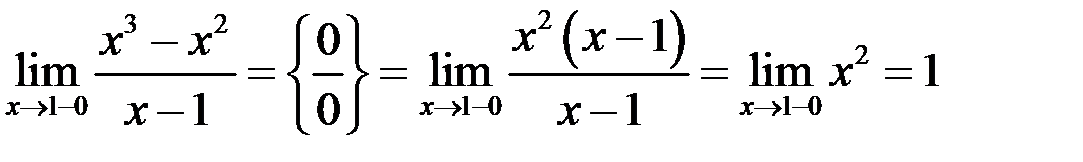
Односторонние пределы конечны и равны. Таким образом, в точке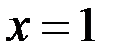 
функция терпит устранимый разрыв.
Как выглядит график данной функции?
Проведем упрощение дроби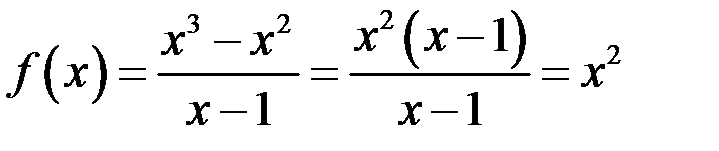 
, и вроде бы получается обычная парабола. Но исходная функция не определена в точке 
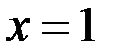, поэтому обязательна следующая оговорка:
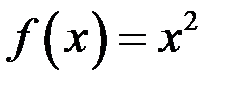, если 
.
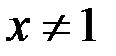Выполним чертёж (рис. 19).
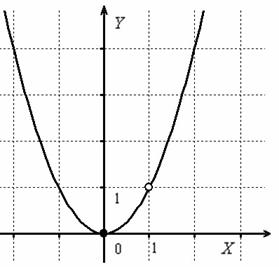Ответ: Функция непрерывна на всей числовой прямой кроме точки 
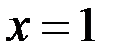, в которой она терпит устранимый разрыв.
Функцию можно доопределить «хорошим» (или иным) способом. Например,
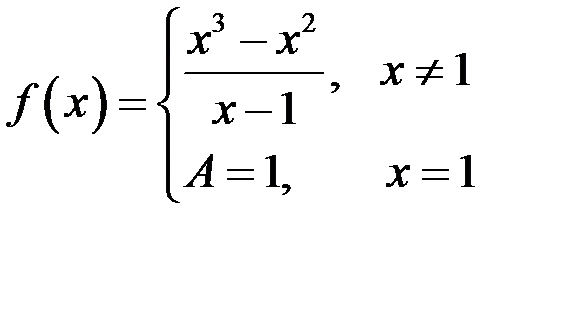и функция
Рис. 19 – График к примеру 8 становится непрерывной. Если же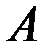 
принимает другое значение, не равное единице, то устранимый разрыв в точке 
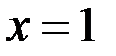остается.
9. Покажем, что функция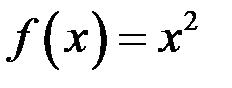 
не является равномерно непрерывной на всей числовой прямой.
Решение. Построим отрицание равномерной непрерывности. Покажем, что существует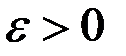 
такое, что для любого положительного 
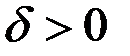найдутся 
такие, что хотя 
.
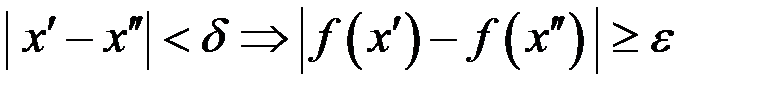Возьмем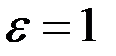 
и любое положительное число 
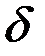. Положим 
, 
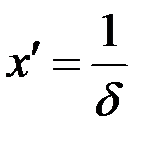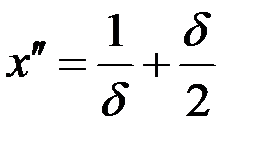. Тогд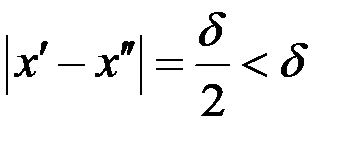а 
, а
.
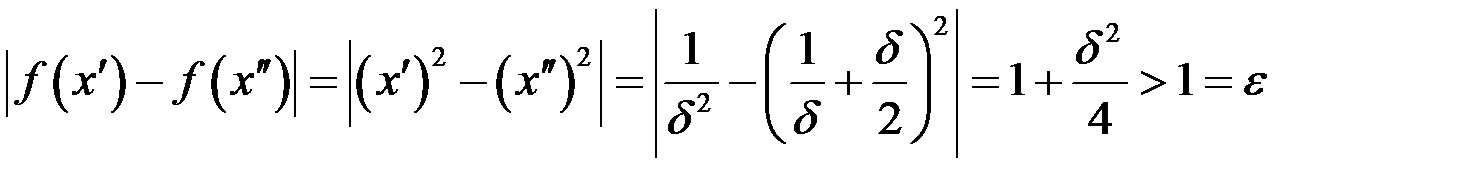Это и означает, что функция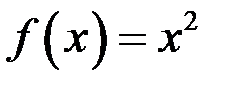 
не является равномерно непрерывной на всей числовой прямой.
10. Найти производную функции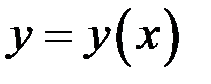 
, заданной неявно 
.
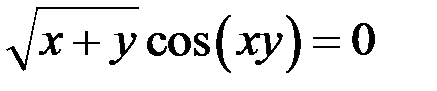Решение. Продифференцируем уравнение, учитывая, что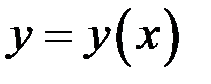 
есть функция от 
.
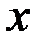Решим уравнение относительно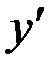 
.
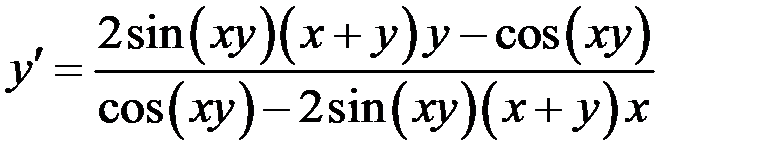
11. Найти вторую производную функции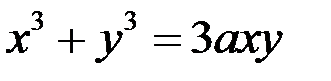 
, заданной неявно.
Решение. Продифференцируем уравнение, учитывая, что 
есть функция от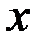 
.
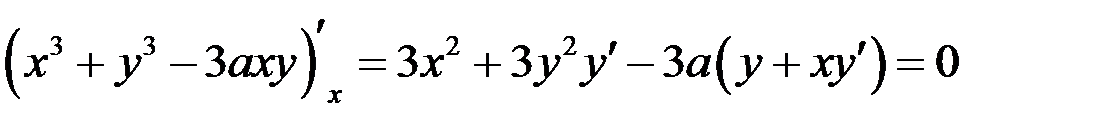
Решим уравнение относительно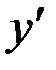 
.
.
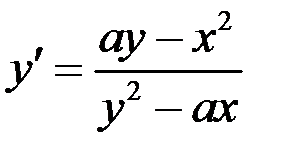Найдем вторую производную, учитывая, что 
есть функция от 
.
.
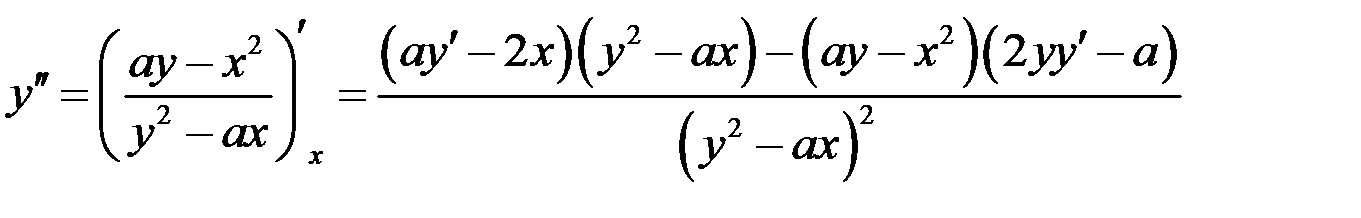Подставляя вместо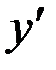 
найденное выражение 
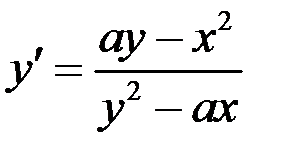получим:
.
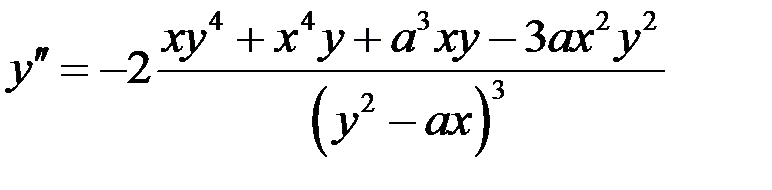12. Найти вторую производную функции 
, заданной параметрически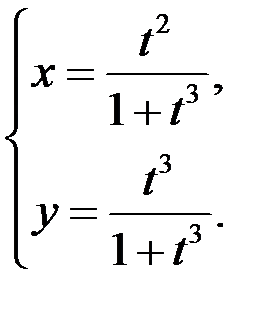 
.
Решение. В случае параметрического задания функции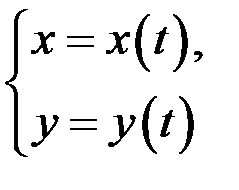 
первая производная вычисляется по формуле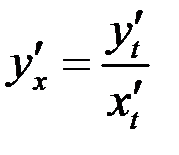 
.
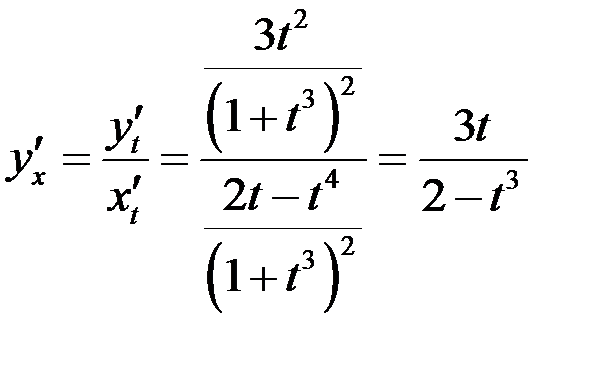Запишем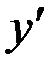 
тоже в параметрической форме вида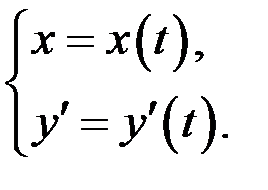 
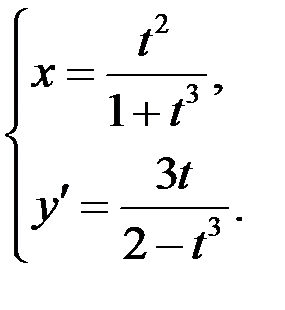
И снова применим формулу вычисления производной, но уже для новой функции 
.
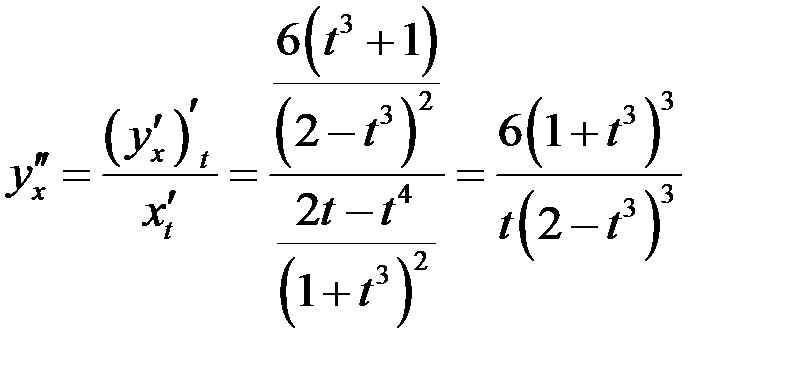
13. Определить значения 
и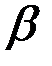 
, при которых функция а) всюду непрерывна, б) всюду дифференцируема:
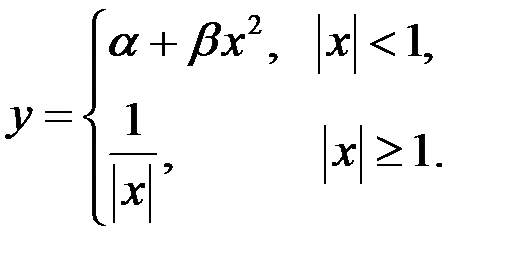
Решение. а) Исследуем на непрерывность. Данная функция является элементарной на интервалах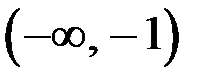 
, 
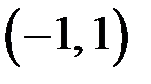и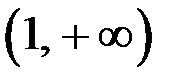 
, а поэтому непрерывна на них. Подозрительными на разрыв являются точки 
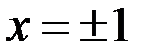. Заметим, что наша функция четна 
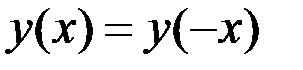, поэтому 
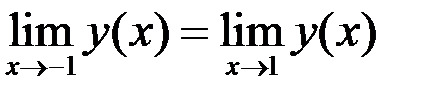и исследования будем проводить в обеих точках одновременно. Для непрерывности необходимо, чтобы односторонние пределы совпадали: 
, 
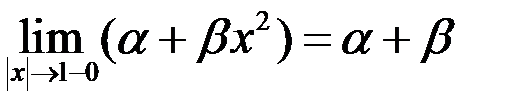. Тогда при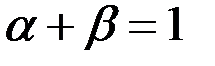 
имеем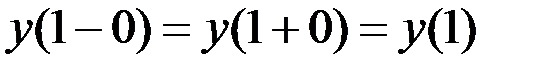 
. Значит, при 
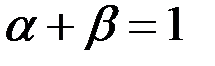данная функция всюду непрерывна.
б) Исследуем на дифференцируемость. Заметим, что на интервалах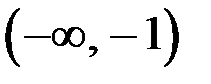 
, 
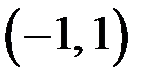и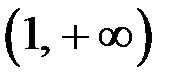 
, функции 
, 
, 
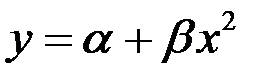, соответственно, имеют производную, а поэтому дифференцируемы. Проверим дифференцируемость в точках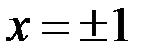 
. Для этого проверим равенство односторонних производных. В точке 
:
, 
, 
.
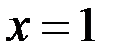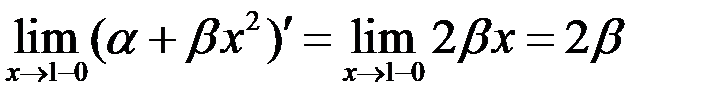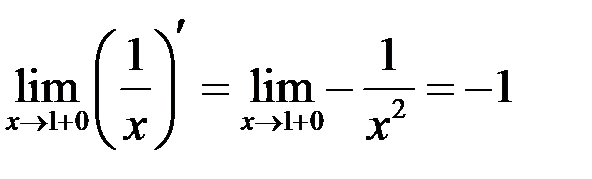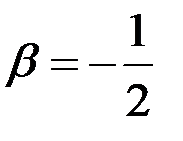В точке 
:
, 
, 
.
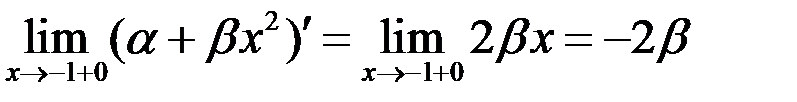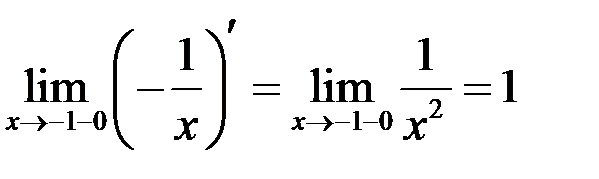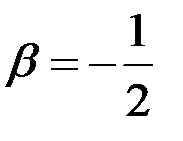Учитывая условие непрерывности функции в точках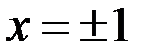 
: 
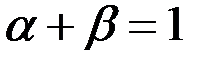, имеем
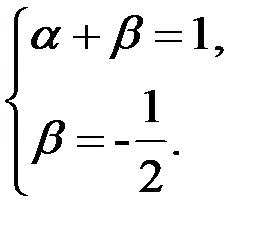. Решив полученную систему, имеем 
, 
.
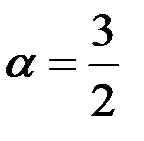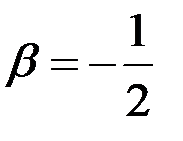Таким образом, при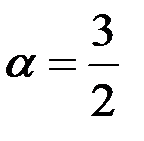 
и 
, функция является всюду непрерывной и всюду дифференцируемой.
14. Написать уравнение касательной и нормали к кривой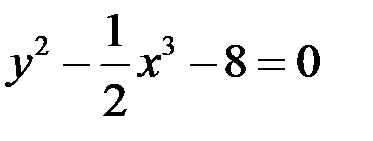 
в точке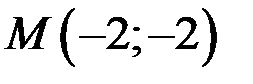 
Решение. Запишем уравнения касательной и нормали в общем виде:
, 
.
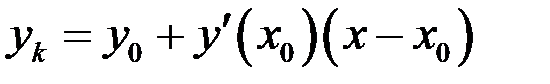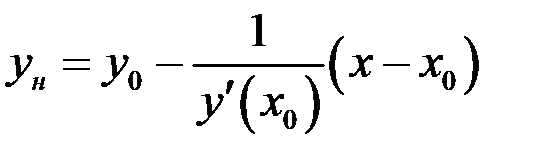Теперь найдем производную. Поскольку функция задана в неявном виде, то производную ищем по формуле:
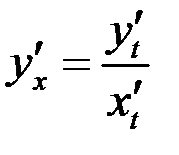
В нашем случае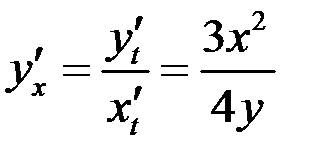 
.
По условию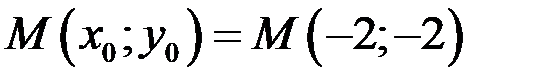 
, следовательно 
.
В результате имеем:
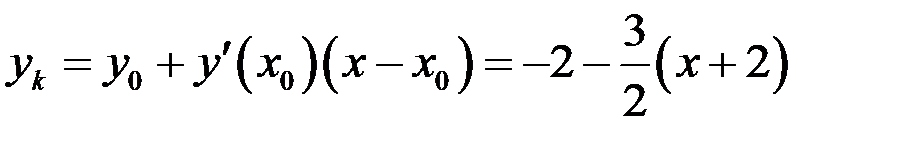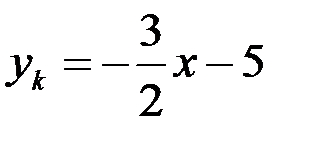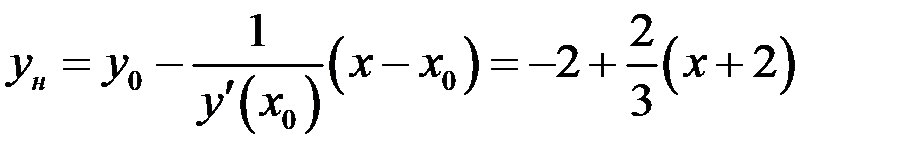или 
.
или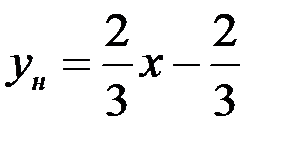 
.
15. Найти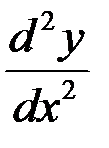 
для функции, заданной параметрически уравнениями:
, 
.
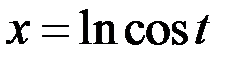Решение. Первую производную найдем по формуле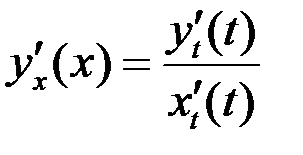 
: 
.
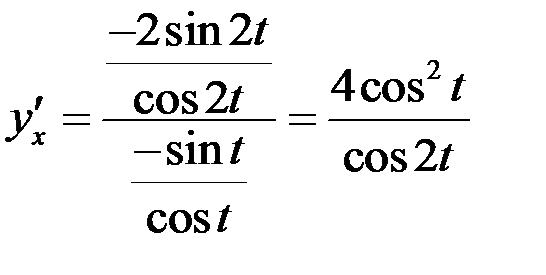Для второй производной формула примет вид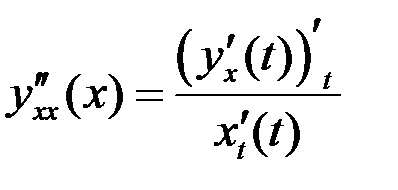 
.
.
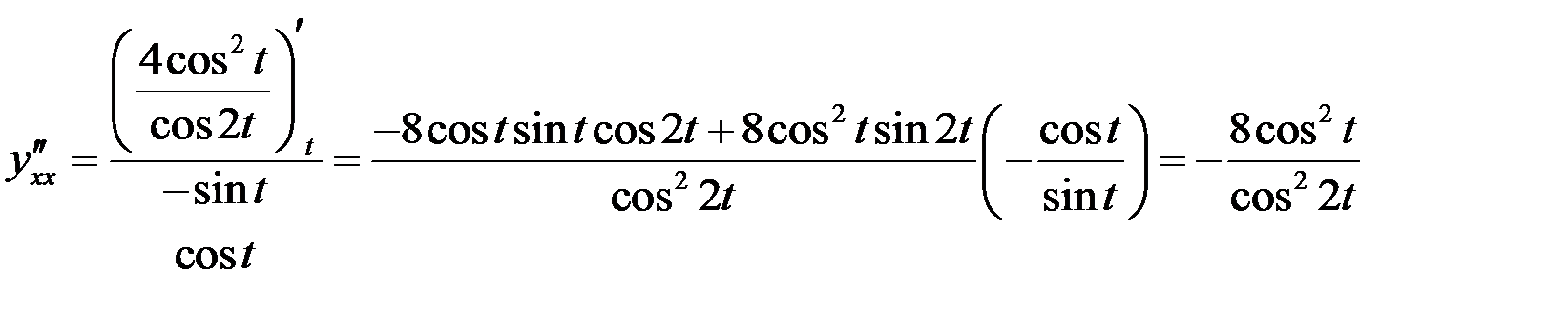Дата: 2018-11-18, просмотров: 515.
