Выделение главной части до первого порядка малости
при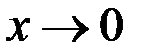

1. .

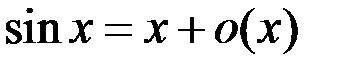2. .

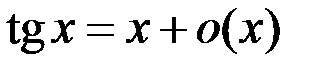3. .

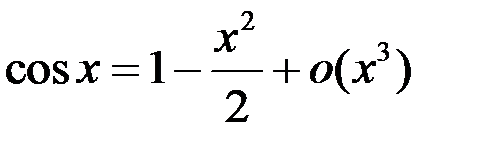4. .

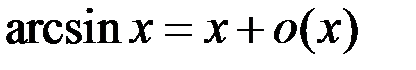5. .

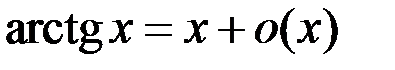6. .

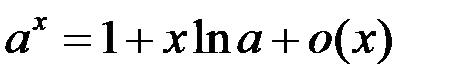7. .

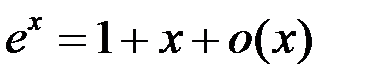8. .

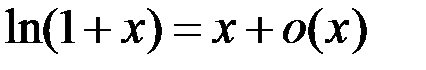9. .

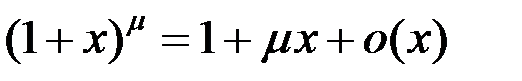10. .

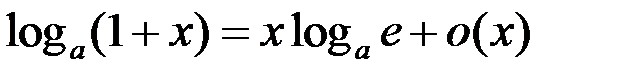Выделение главной части до второго порядка малости
при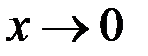

1. .

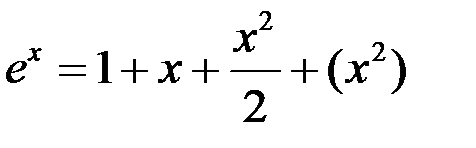2. .

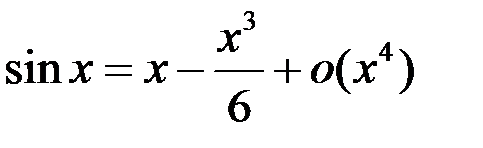3. .

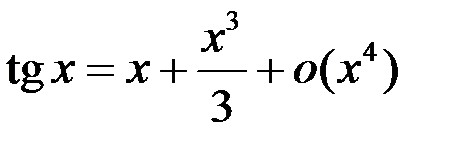4. .

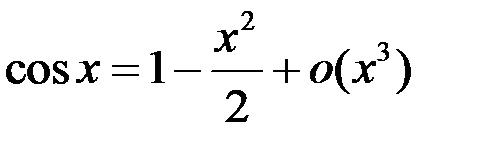5. .

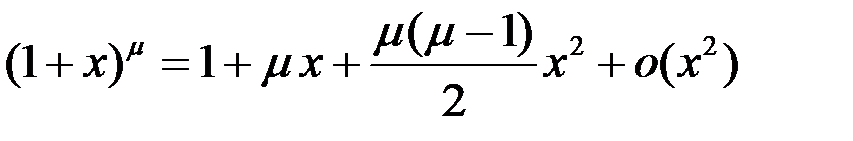6. .

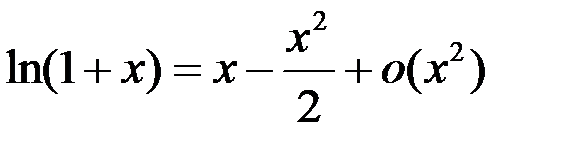7. .

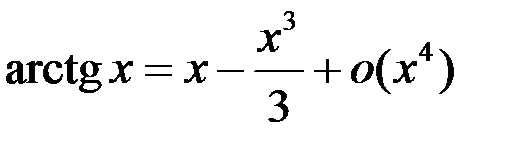Замечание. Если при вычислении пределов выполняются действия умножения и деления, то можно пользоваться таблицей эквивалентных функций. Если необходимо еще выполнять действия сложения или вычитания, то необходимо использовать асимптотические таблицы.

Теорема. Если существует 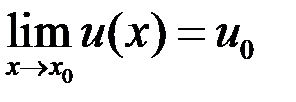 и существует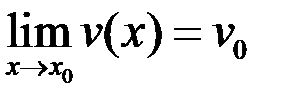 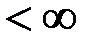, то существует .

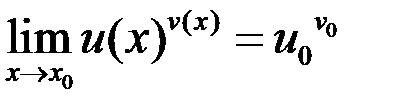Непрерывные функции

Определение. Функция называется непрерывной в точке 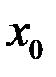, если она определена в этой точке и .

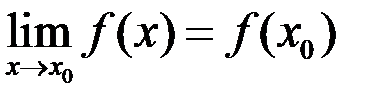Если ввести обозначения 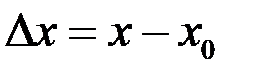, , 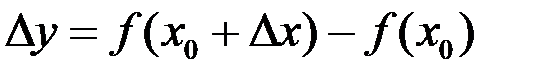то определение непрерывной функции можно переформулировать.

Определение. Функция называется непрерывной в точке 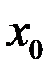, если .

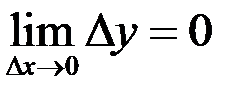Заметим, что формула 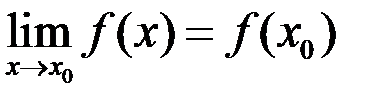 несет такую информацию:

1) ;

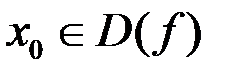2) 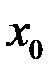 – предельная точка ;

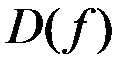3) ;

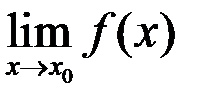4) этот предел конечен;

5) .

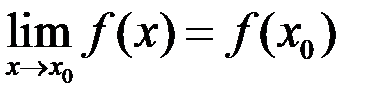На языке 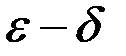 определение звучит так:

,

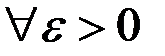
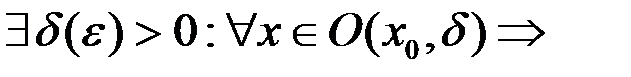
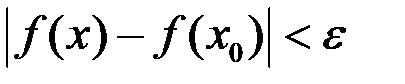или, используя знак неравенства

.

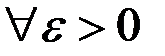
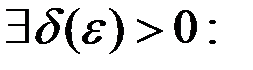
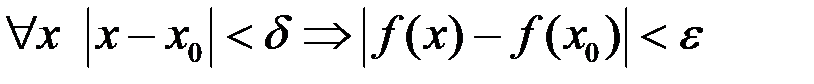Укажем некоторые свойства функций, непрерывных в точке.

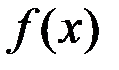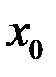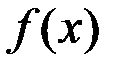Свойство 1. Если  непрерывна в точке , то  ограничена в некоторой окрестности точки .

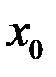Свойство 2. Если 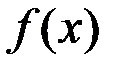 непрерывна в точке  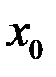и 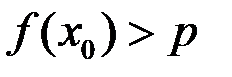, то существует окрестность точки 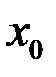, в которой .

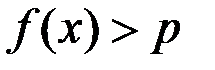Свойство 3. Если 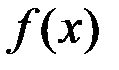 непрерывна в точке  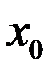и 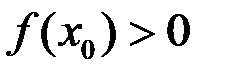, то существуют  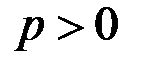и 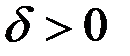, такие, что  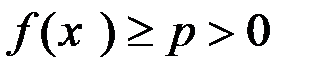в 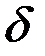 – окрестности точки .

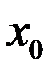Свойство 4. Арифметические операции с непрерывными функциями.

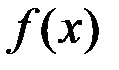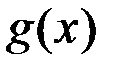Если  и  непрерывны в точке 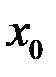, то 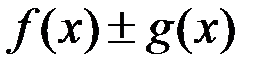, 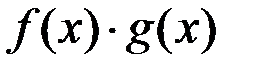; ; 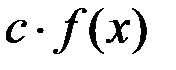 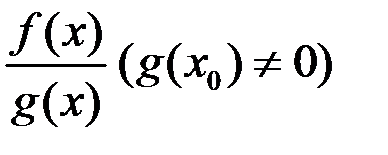также непрерывны в точке .

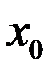Определение. 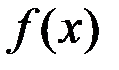 непрерывна на множестве 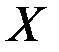, если она непрерывна в каждой точке .

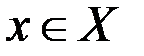Примеры непрерывных функций:

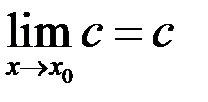
1)  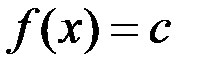– непрерывна на .

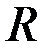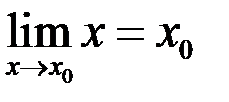
2)  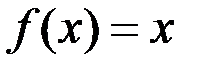– непрерывна на .

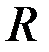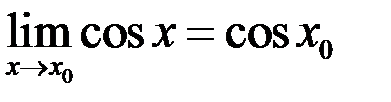
3)  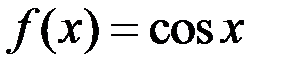– непрерывна на .

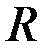4) 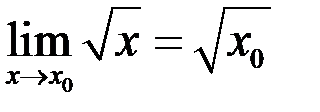 (  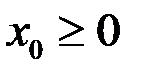)  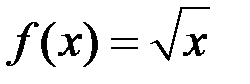– непрерывна на .

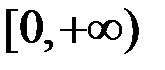Непрерывность элементарных функций

Определение. Основными элементарными функциями будем считать .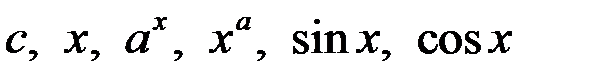

Определение. Функции, которые образуются из основных элементарных с помощью: 1) конечного числа арифметических операций; 2) обращения; 3) суперпозиции (сложная функция) называются элементарными.

Таким образом, элементарными являются все многочлены, рациональные дроби, алгебраические функции (то есть содержащие степенные функции с рациональными показателями-радикалами), показательная, логарифмическая, прямые и обратные тригонометрические.

Вопрос о непрерывности элементарных функций решается следующей теоремой.

Теорема. Все элементарные функции непрерывны на своей области определения.

Классификация точек разрыва

Сначала введем понятие односторонней непрерывности.

Определение. Функция называется непрерывной справа, если .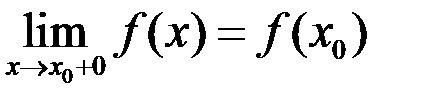

Определение. Функция называется непрерывной слева, если .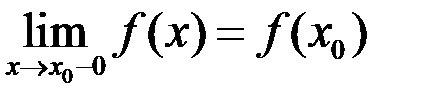

Из последних определений следует критерий непрерывности.

Теорема (критерий непрерывности функции в точке). Для того, чтобы функция была непрерывна в точке, необходимо и достаточно, чтобы она была непрерывна справа и слева одновременно.

Определение. Точкой разрыва функции называют точку 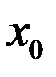, в которой нарушается одно из трёх условий непрерывности: а) функция  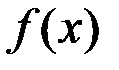определена в точке и её окрестности; б) существует конечный предел функции  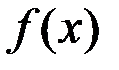в точке 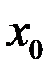; в) этот предел равен значению функции в точке .

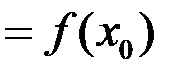Классификация точек разрыва

1) Точка 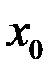 называется точкой устранимого разрыва, если в этой точке существуют конечные односторонние пределы и они равны.

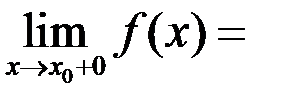
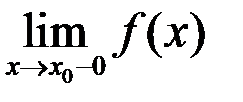
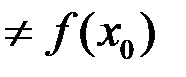 (значение  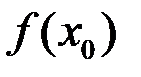может и не существовать).

2) Точка 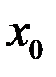 называется точкой разрыва 1-го рода (скачок), если односторонние пределы существуют, конечны, но не равны между собой .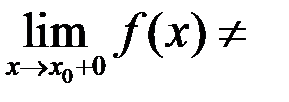

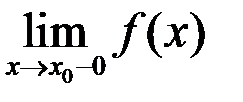3) Точка 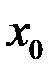 называется точкой разрыва 2-го рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.

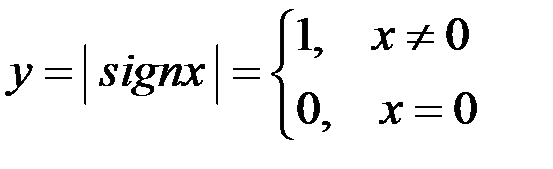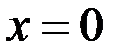Пример 1.  точка  – точка устранимого разрыва.

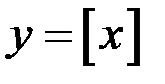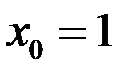
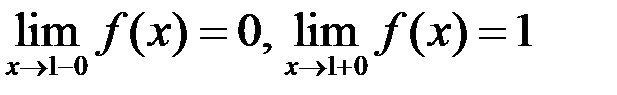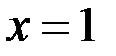Пример 2. ,   точка  – точка разрыва 1-го рода. Величина скачка 1.

Пример 3. 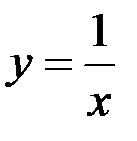 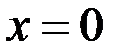– точка разрыва 2-го рода, , .

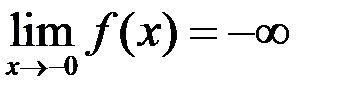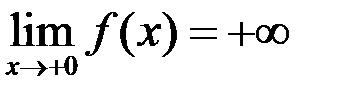Пример 4. 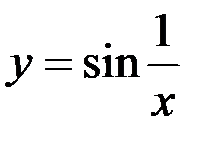,  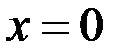– точка разрыва 2-го рода.

Покажем, что функция 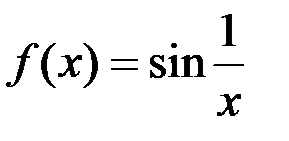 при 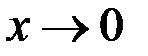 не имеет предела, то есть не существует .

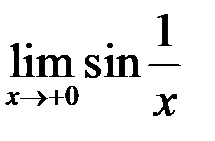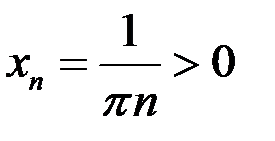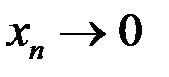
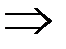
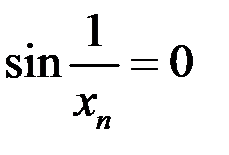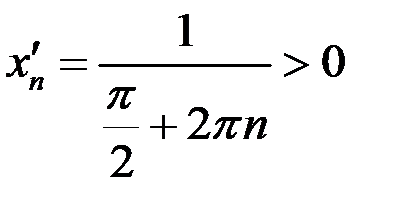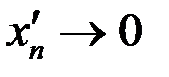
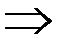
Возьмем две последовательности точек , , и , 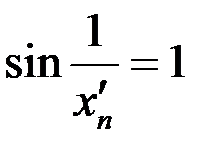. Две последовательност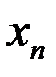и  и 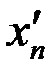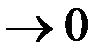, но функция в этих точках 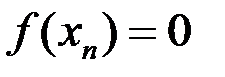, 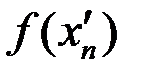=1, то есть последовательности значений функции стремятся к различным значениям, общего предела нет, ни одностороннего, ни двухстороннего. Отсюда следует, по определению Гейне, что функция  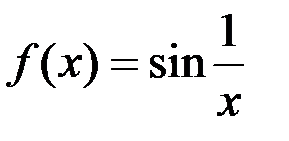в точке  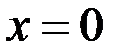не имеет предела.