Рассмотрим особые случаи, которые могут встретиться при изучении производных.
Сначала рассмотрим односторонние производные. Пусть функция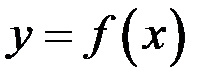 
задана на отрезке 
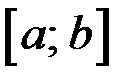. Тогда при исчислении предела выражения 
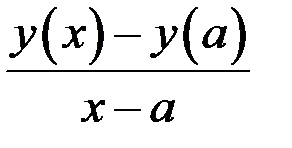в точке 
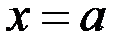мы должны ограничиться приближением 
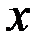к 
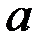только справа, а, в случае точки 
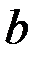, – слева. В этом случае говорят об односторонней производной. В соответствующих точках график функции 
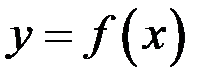должен иметь «одностороннюю» касательную.
Определение. Если функция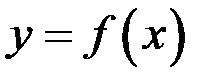 
определена в правой полуокрестности (соответственно, левой полуокрестности) точки 
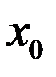и существует предел 
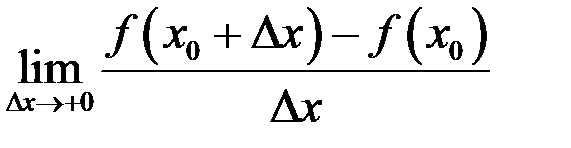(соответственно, 
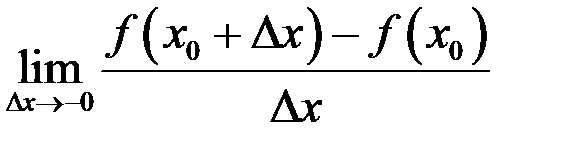), то она называется правой производной (соответственно, левой) функции 
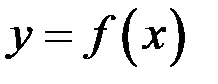в точке 
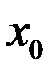и обозначается 
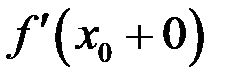(соответственно, 
).
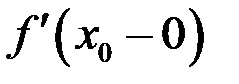Может случиться так, что и для внутренней точки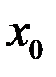 
существуют только односторонние пределы разностного отношения 
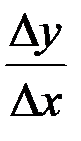(при 
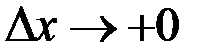или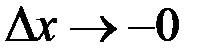 
), которые не равны между собой. Их также называют односторонними производными. Для графика функции в соответствующей точке будут существовать только односторонние касательные, образующие угол; а точка будет угловой.
Теорема. Для того чтобы функция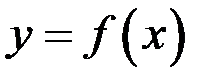 
, определенная в некоторой окрестности точки 
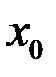имела производную 
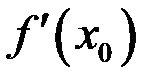, необходимо и достаточно, чтобы существовали односторонние производные в точке 
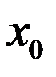и они были равны 
.
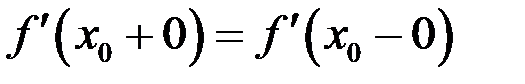Пример 1. Для функции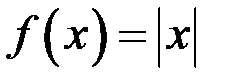 
, найти односторонние производные в точке 
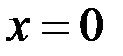(рис. 12).
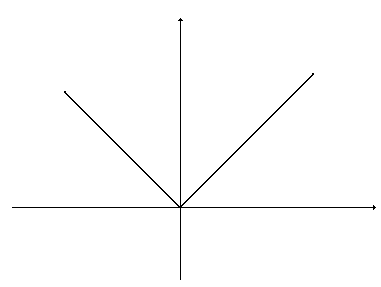Решение. Ранее (см. пример 8 на стр.52) мы выяснили, что данная функция в точке 
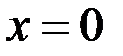производной не имеет. Найдем односторонние производные в этой точке (если они существуют).
Разностное отношение может принимать значения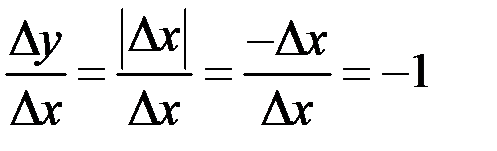 
при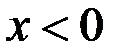 
и Рис. 12 – Пример 1 
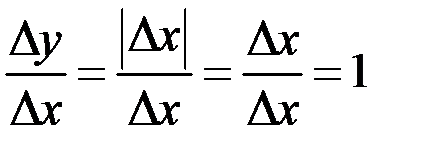при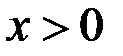 
. Переходя к пределу получаем односторонние производные в нуле 
, 
.
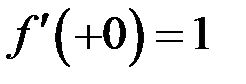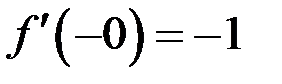Бесконечные производные
Если отношение приращени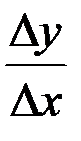й 
при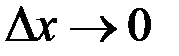 
стремится к 
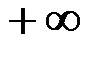(или к 
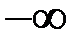) то это значение также называют производной и обозначают как обычно.
Аналогично вводится понятие об односторонней бесконечной производной.
Геометрический смысл бесконечной производной заключается в том, что касательная параллельна оси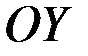 
.
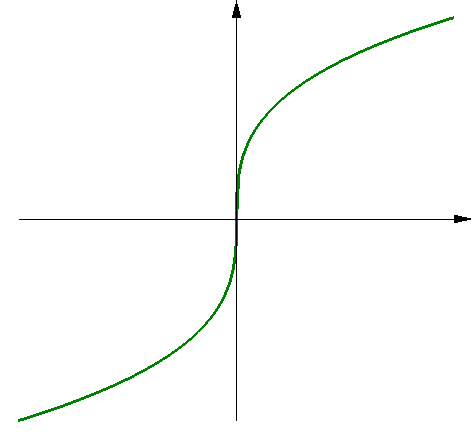
Пример 2. Вычислить производную функции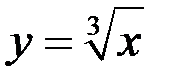 
в точке 
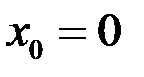(рис. 13).
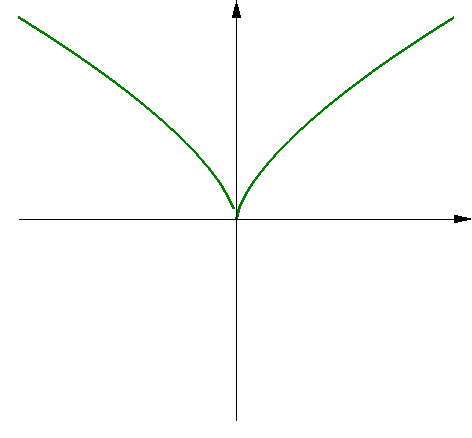Рис. 13 – Пример 2 Решение. Односторонние пределы оказались равны 
.
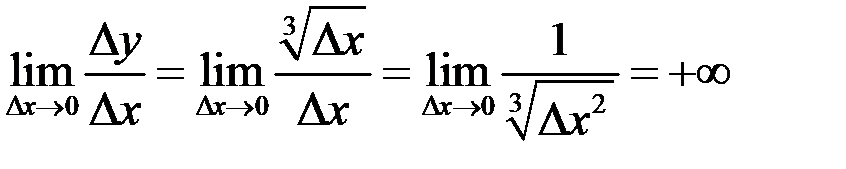Пример 3. Вычислить производную функции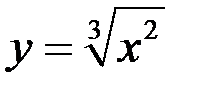 
в точке 
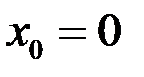(рис. 14).
Решение. Односторонние пределы дают разный результат
Рис. 14 – Пример 3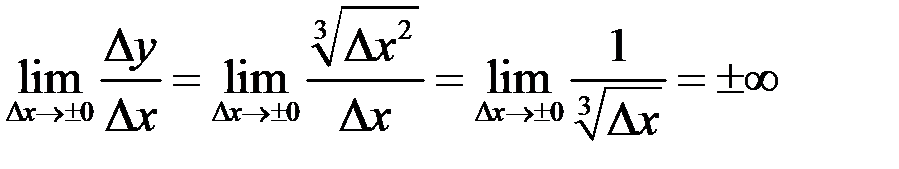 
.
Задачи для самостоятельного решения.
Доказать или опровергнуть следующие утверждения.
1. Если функция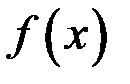 
имеет, а функция 
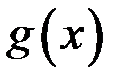не имеет производной в некоторой точке, то 
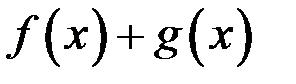не имеет производной в этой точке.
2. Если функци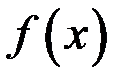и 
и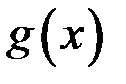 
не имеют производной в некоторой точке, то и функция 
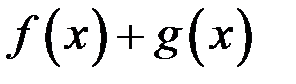не имеет производной в этой точке.
3. Если функция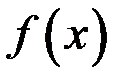 
имеет, а функция 
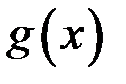не имеет производной в некоторой точке, то 
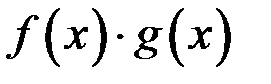не имеет производной в этой точке.
4. Если функци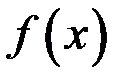и 
и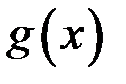 
не имеют производной в некоторой точке, то и функция 
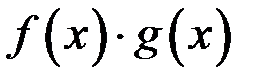не имеет производной в этой точке.
Дифференциал, дифференцируемость
Определение. Пусть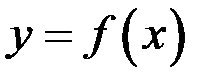 
определена в точке 
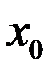и некоторой ее окрестности 
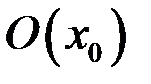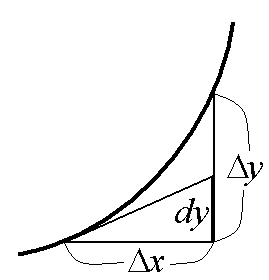
. Если прирост функции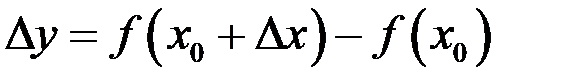 
в этой точке можно записать в ви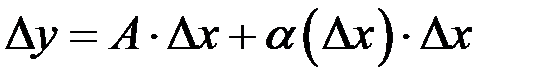де 
, где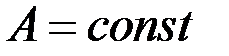 
, 
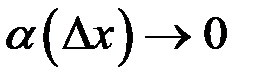Рис. 15 – Дифференциал при 
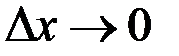, то говорят, что функция дифференцируема в точке 
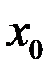(рис. 15).
Определение. При такой записи главную линейную часть приращения дифференцируемой функции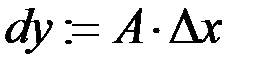 
называют дифференциалом функции в точке 
.
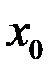Дифференциал представляет собой линейную функцию от приращения аргумента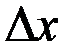 
. При этом 
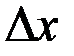– произвольное значение, не обязательно б.м. Кроме того, дифференциал 
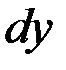отличается от приращения функции 
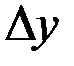на величину, б.м. относительно 
.
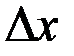Теорема. (О связи между дифференцируемостью и существованием производной). Для того чтобы функция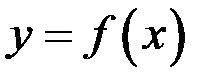 
в точке 
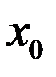была дифференцируема, необходимо и достаточно, чтобы для нее в этой точке существовала конечная производная 
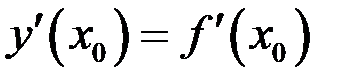. При этом в записи формулы дифференциала 
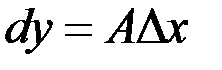имеем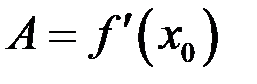 
.
Замечание. Ранее, на стр.15 мы дали другое определение дифференцируемости функции, а именно: функция, имеющая производную в точке, называется дифференцируемой в этой точке. Теорема, доказанная нами, устанавливает равносильность этих понятий.
Следствие из теоремы. Считается, что дифференциал независимой переменной равен ее приращению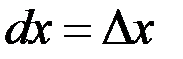 
(если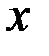 
– независимая переменная).
На основании этого результата дифференциал функции будем записывать следующим образом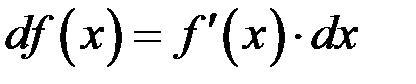 
.
Замечание. Дифференциал функции зависит от двух переменных – от самой точки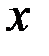 
и от ее приращения.
Дата: 2018-11-18, просмотров: 859.
