Теорема (1-я теорема Больцано–Коши). Если функция 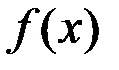 непрерывна на отрезке
непрерывна на отрезке 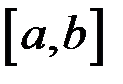 и на концах принимает значения разных знаков, то найдется точка
и на концах принимает значения разных знаков, то найдется точка 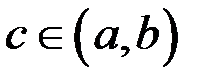 такая, что
такая, что 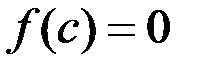 (рис. 3).
(рис. 3).
Доказательство. Пусть для определенности 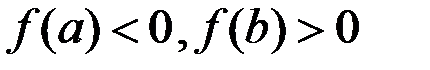 .
.
 Делим отрезок
Делим отрезок 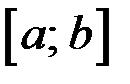 пополам точкой
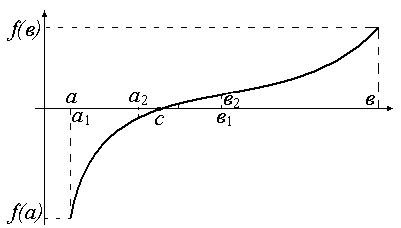
пополам точкой 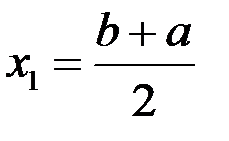 . Если посредине отрезка
. Если посредине отрезка 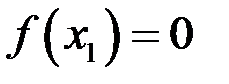 , то теорема доказана, если нет, то выбираем ту половину отрезка, на концах которой функция принимает
, то теорема доказана, если нет, то выбираем ту половину отрезка, на концах которой функция принимает
Рис. 3 – Теорема Больцано–Коши значения разных знаков. Выбранный отрезок 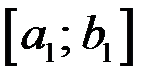 вновь делим пополам точкой
вновь делим пополам точкой 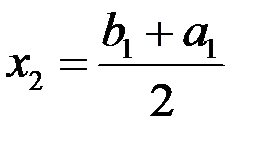 . Если посредине нового отрезка
. Если посредине нового отрезка 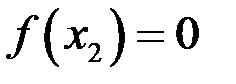 , то теорема доказана, если нет, то выбираем ту половину от этой половины, на концах которой функция принимает значения разных знаков. Продолжим этот процесс до бесконечности (либо на каком-то этапе попадем в точку
, то теорема доказана, если нет, то выбираем ту половину от этой половины, на концах которой функция принимает значения разных знаков. Продолжим этот процесс до бесконечности (либо на каком-то этапе попадем в точку 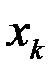 такую, что
такую, что 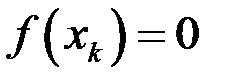 , что приведет к досрочному завершению доказательства). Получим систему вложенных отрезков, длины которых стремятся к нулю при
, что приведет к досрочному завершению доказательства). Получим систему вложенных отрезков, длины которых стремятся к нулю при 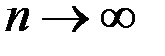 :
: 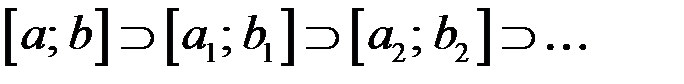 с условием, чтобы
с условием, чтобы 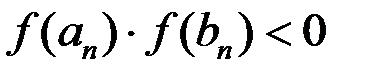 ,
, 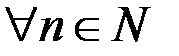 .
.
По теореме Кантора (о вложенных отрезках) 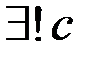
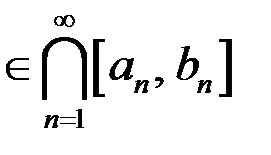 . А согласно замечанию к теореме Кантора
. А согласно замечанию к теореме Кантора 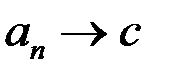 ,
, 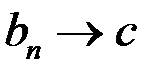 .
.
Из свойства непрерывности функции следует 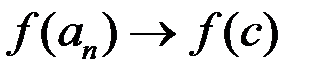 ,
, 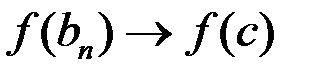 . По теореме о предельном переходе имеем
. По теореме о предельном переходе имеем
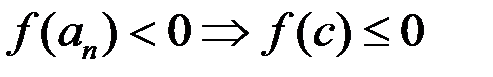
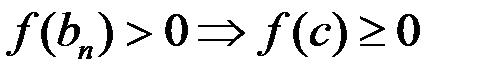
 получили
получили 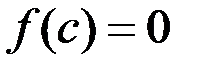 . Теорема доказана.
. Теорема доказана.
Так как в процессе доказательства искомая точка строится (ищется), то такое доказательство называется конструктивным.
Такая точка может быть не одна, но по крайней мере одна найдется!
Следствие (2-я теорема Больцано–Коши). Пусть функция 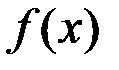 непрерывна на отрезке
непрерывна на отрезке 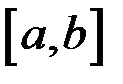 и на концах принимает конечные, но не равные значения
и на концах принимает конечные, но не равные значения 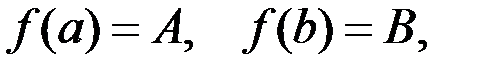 тогда
тогда 
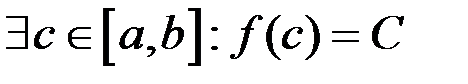 .
.
Задачи для самостоятельного решения
1. Доказать, что любой многочлен нечетной степени имеет хотя бы один действительный корень.
2. Доказать, что если многочлен четной степени принимает хотя бы одно значение, противоположное по знаку коэффициенту старшего члена, то он имеет не менее двух действительных корней.
3. Пусть функции 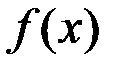 и
и 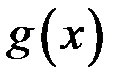 определены и непрерывны на отрезке
определены и непрерывны на отрезке 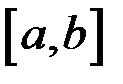 и
и 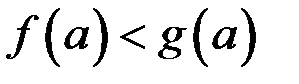 ,
, 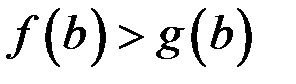 . Доказать, что существует точка
. Доказать, что существует точка 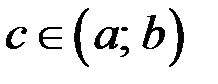 такая, что
такая, что 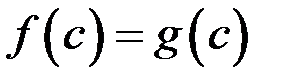 .
.
4. Функция 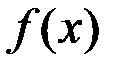 непрерывна на отрезке
непрерывна на отрезке 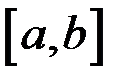 . Доказать, что функции
. Доказать, что функции 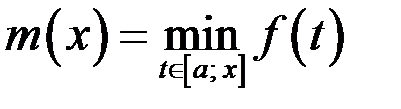 и
и 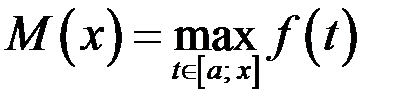 непрерывны на
непрерывны на 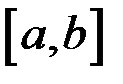 .
.
5. Пусть функции 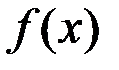 и
и 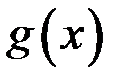 непрерывны на отрезке
непрерывны на отрезке 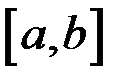 . Доказать, что функции
. Доказать, что функции 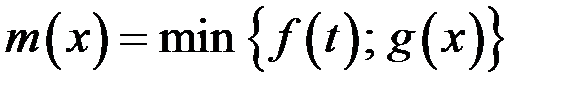 и
и 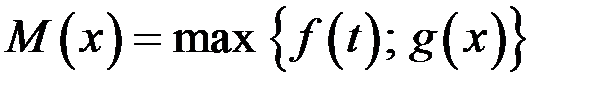 непрерывны на
непрерывны на 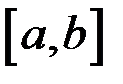 .
.
Теоремы о непрерывности монотонной, сложной и обратной функций
Теорема. Монотонная функция имеет точки разрыва 1-го рода, то есть скачки.
Следствие. Если функция монотонна на 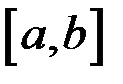 и область значений функции заполняет отрезок
и область значений функции заполняет отрезок 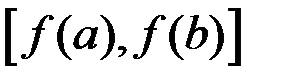 , то
, то 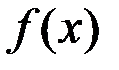 непрерывна.
непрерывна.
Теорема. Если в точке 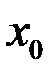 функция
функция 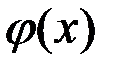 непрерывна, а в точке
непрерывна, а в точке 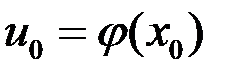 функция
функция 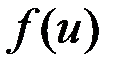 непрерывна, то
непрерывна, то 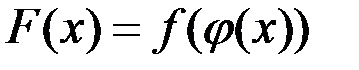 непрерывна в точке
непрерывна в точке 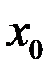 .
.
Теорема (о существовании обратной функции). Если функция 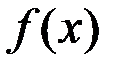 :
:
1) определена на отрезке 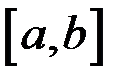 ;
;
2) строго монотонна на 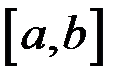 ;
;
3) непрерывна на 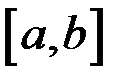 ;
;
тогда
1¢) для 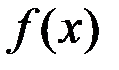 существует обратная, определенная на
существует обратная, определенная на 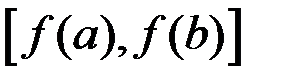 (если
(если 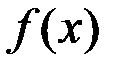 возрастает);
возрастает);
2¢) 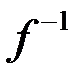 строго монотонна (тоже возрастает);
строго монотонна (тоже возрастает);
3¢) 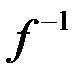 непрерывна на
непрерывна на 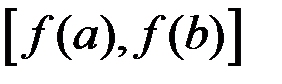 .
.
Дата: 2018-11-18, просмотров: 572.