 Диалог между водителем женщиной и полицейским.
Диалог между водителем женщиной и полицейским.
- Мадам, Вы нарушили правила дорожного движения. Вы ехали со скоростью 90 км/час.
- Простите, это невозможно. Как я могла проехать 90 км за час, если я еду всего лишь 7 минут.
- Я имею в виду, мадам, что если бы Вы продолжали бы ехать таким же образом, то через час Вы бы проехали 90 км.
- Если бы я продолжала ехать, как ехала, еще час, то налетела бы на стенку в конце улицы!
- Ваш спидометр показывал 90 км/час.
- Мой спидометр и давно не работает.
Пример объяснения понятия скорости, взятый из Фейнмановских лекций по физике ( Башмаков, 10-11 класс Алгебра и начала анализа).
Попытаемся ответить на вопрос, «что такое скорость?» не ссылаясь на число, показываемое спидометром, а используя понятия расстояния и времени.
Пусть частица, например автомобиль, движется по прямолинейной дороге. И пусть задано уравнение – закон движения 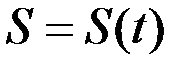 , то есть мы знаем пройденный путь в любой момент времени
, то есть мы знаем пройденный путь в любой момент времени 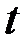 .
.
Пусть в момент 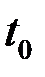 частица находится в точке
частица находится в точке 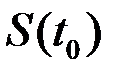 , а в момент
, а в момент 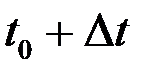 – в точке
– в точке  . То есть за время
. То есть за время 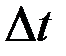 было пройдено расстояние
было пройдено расстояние 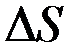 .
.
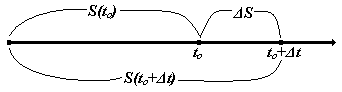 Отношение
Отношение  выразит среднюю скорость
выразит среднюю скорость 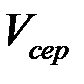 за время
за время 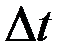 (рис. 7).
(рис. 7).
Рис. 7 – Скорость А мгновенная скорость в момент 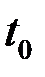 получится отсюда предельным переходом
получится отсюда предельным переходом
 .
.
Мы рассмотрели две задачи, и, если отвлечься от геометрического и механического смысла, то мы, по существу, делали одну и ту же операцию: приращение функции делили на приращение независимой переменной и вычисляли предел их отношения.
Таким образом, мы приходим к основному понятию дифференциального исчисления – понятию производной.
Определение производной
Определение. Пусть функция  определена в некоторой окрестности
определена в некоторой окрестности 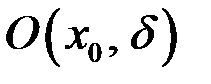 точки
точки 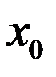 , и пусть приращение
, и пусть приращение  . Предел отношения приращения функции к приращению аргумента называется производной
. Предел отношения приращения функции к приращению аргумента называется производной
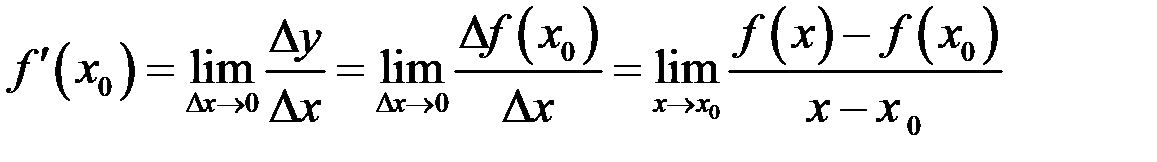
(здесь мы обозначили 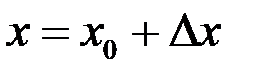 ). Другие обозначения:
). Другие обозначения:
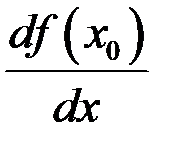 ,
, 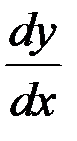 (обозначения Лейбница),
(обозначения Лейбница), 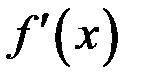 ,
, 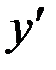 (обозначения Лагранжа).
(обозначения Лагранжа).
Пользуясь только что введенным понятием, можно определить геометрический и механический смысл производной.
Геометрический смысл: Производная функции 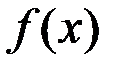 в точке
в точке 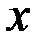 численно равна тангенсу угла наклона касательной к графику этой функции построенной в точке
численно равна тангенсу угла наклона касательной к графику этой функции построенной в точке  с положительным направлением с осью
с положительным направлением с осью 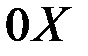 .
.
Механический смысл: Производная равна скорости изменения (роста) функции в точке 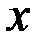 .
.
Из определения производной следует в случае убывающей функции производная отрицательная. Это объясняется тем, что 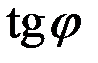 будет отрицательным, если
будет отрицательным, если 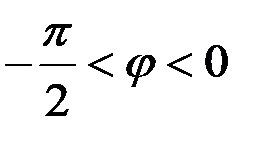 . На этом свойстве производной базируется исследование поведения функции на рост (падение) на заданном отрезке.
. На этом свойстве производной базируется исследование поведения функции на рост (падение) на заданном отрезке.
Определение. Касательной к графику функции 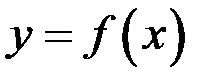 в точке
в точке 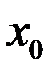 называется прямая, задаваемая уравнением
называется прямая, задаваемая уравнением  проходящая через точку
проходящая через точку 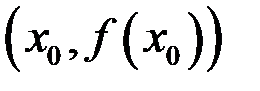 и имеющая коэффициент наклона
и имеющая коэффициент наклона 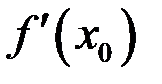 .
.
 Определение. Прямая, проходящая через точку
Определение. Прямая, проходящая через точку 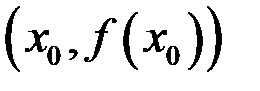 и перпендикулярная касательной, называется нормалью к графику функции в этой точке. Ее уравнение
и перпендикулярная касательной, называется нормалью к графику функции в этой точке. Ее уравнение  .
.
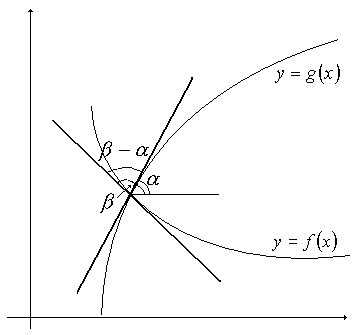
Определение. Будем считать углом между кривыми 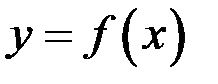 и
и 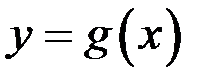 в точке пересечения
в точке пересечения 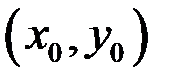 , где
, где 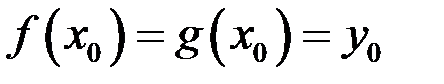 , угол между касательными к кривым
, угол между касательными к кривым 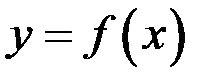 и
и 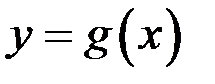 в этой точке (рис. 8). Обозначим
в этой точке (рис. 8). Обозначим 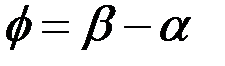 , тогда
, тогда
Рис. 8 – Угол между кривыми 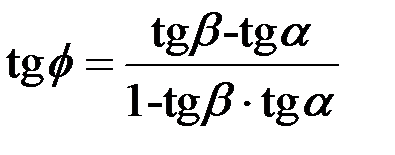 ,
, 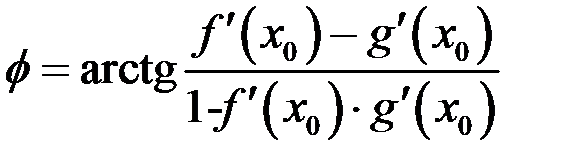 .
.
Наше определение производной конструктивно, то есть показывает, как можно вычислить производную функции в данной точке.
Если же удается каждому числу 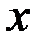 из области определения функции
из области определения функции  поставить в соответствие значение
поставить в соответствие значение 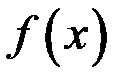 , то это правило определит новую функцию на области определения
, то это правило определит новую функцию на области определения 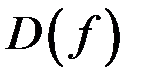 , а именно, производную функции на множестве; то есть производная – новая функция.
, а именно, производную функции на множестве; то есть производная – новая функция.
При этом процесс вычисления производной функции называется дифференцированием.
Определение. Функция, имеющая производную в точке 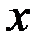 , называется дифференцируемой в этой точке. Если функция имеет производную в каждой точке интервала, то она называется дифференцируемой в интервале.
, называется дифференцируемой в этой точке. Если функция имеет производную в каждой точке интервала, то она называется дифференцируемой в интервале.
При этом процесс вычисления производной функции называется дифференцированием.
Примеры нахождения производной по определению
Пример 1.  ,
, 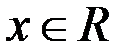 .
.
Так как 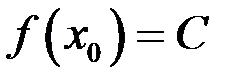 и
и 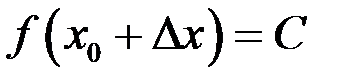 , то
, то 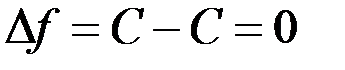 . Имеем
. Имеем  , то есть
, то есть 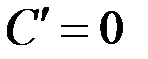 .
.
Пример 2.  ,
, 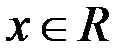 .
.
Так как  и
и 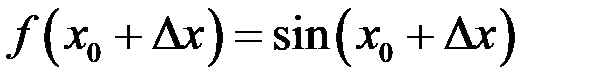 , то
, то 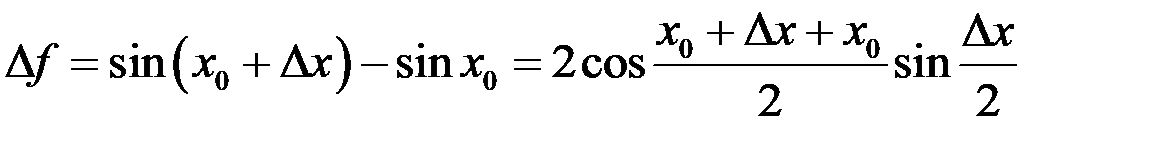 .
.
Имеем 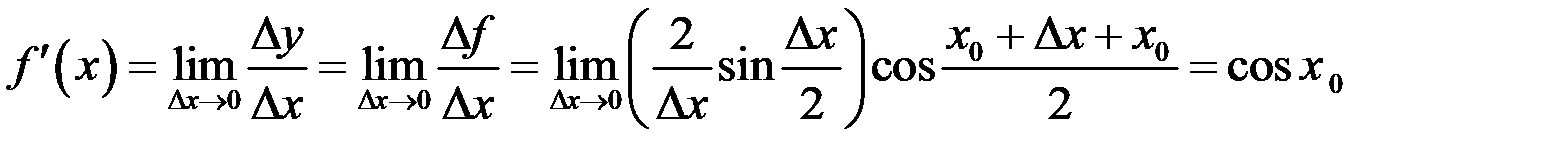 . Здесь мы использовали что
. Здесь мы использовали что  (непрерывность функции косинус), и
(непрерывность функции косинус), и 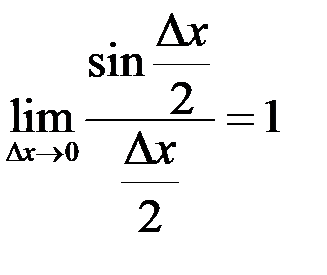 (первый замечательный предел). В результате имеем
(первый замечательный предел). В результате имеем 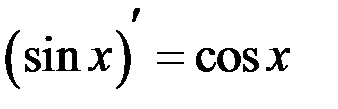 .
.
Пример 3. 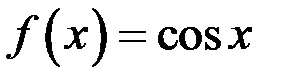 ,
, 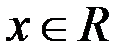 .
.
Так как 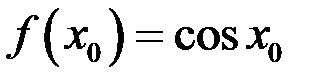 и
и 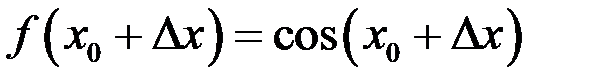 , то
, то  . Имеем
. Имеем 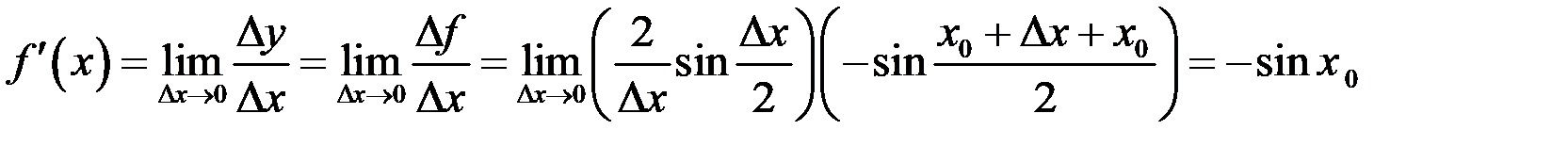 . Здесь, по аналогии с предыдущим примером, мы использовали что
. Здесь, по аналогии с предыдущим примером, мы использовали что 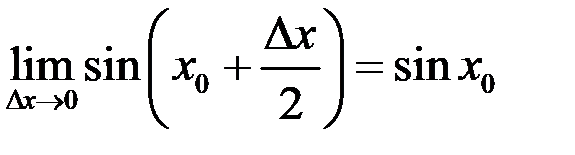 (непрерывность функции синус), и
(непрерывность функции синус), и 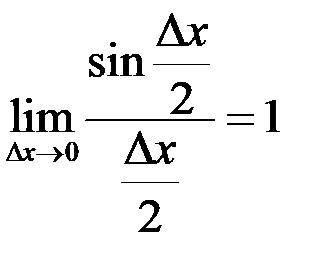 (первый замечательный предел). Имеем
(первый замечательный предел). Имеем 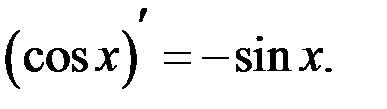
Пример 4. 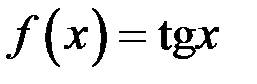 ,
, 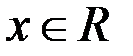 .
.
Так как 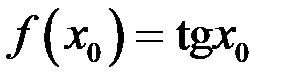 и
и 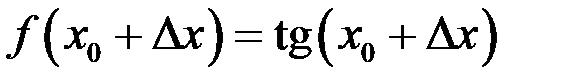 , то
, то 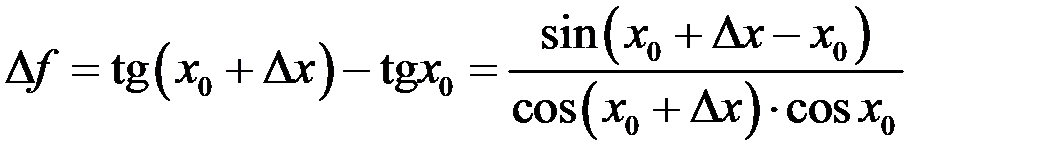 . (Здесь мы воспользовались формулой
. (Здесь мы воспользовались формулой 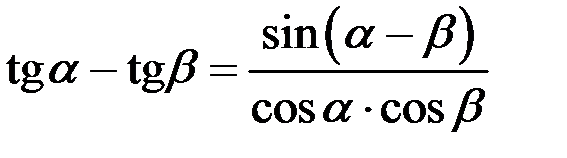 ).
).
Имеем 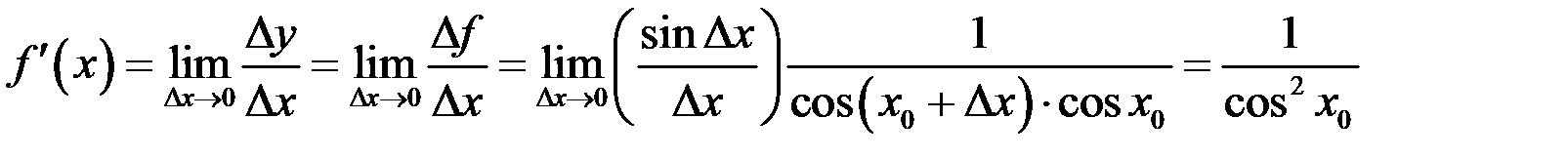 . Здесь, по аналогии с предыдущими примерами, мы использовали что
. Здесь, по аналогии с предыдущими примерами, мы использовали что 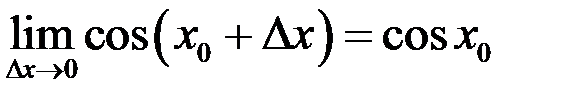 (непрерывность функции косинус), и
(непрерывность функции косинус), и  (первый замечательный предел). Таким образом
(первый замечательный предел). Таким образом 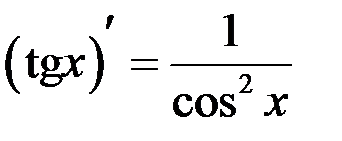 .
.
Пример 5. 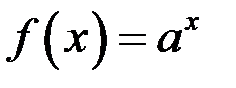 ,
, 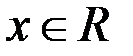 .
.
Так как 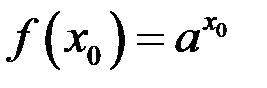 и
и  , то
, то 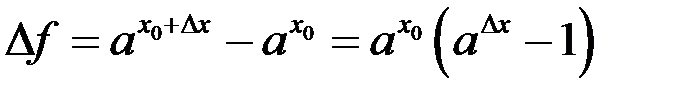 . Имеем
. Имеем 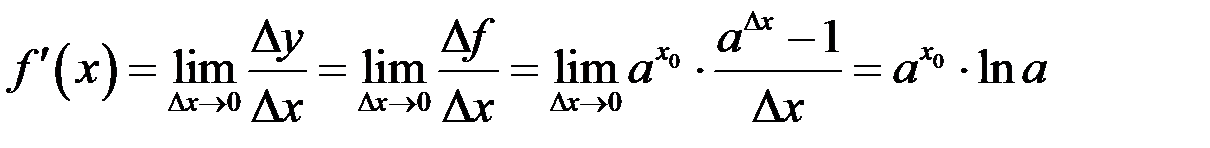 . Здесь мы использовали следствие из второго замечательного предела
. Здесь мы использовали следствие из второго замечательного предела 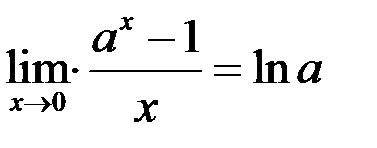 . То есть
. То есть 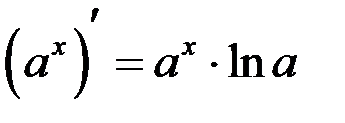 .
.
Пример 6. 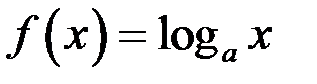 ,
,  .
.
Так как 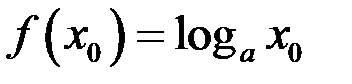 и
и 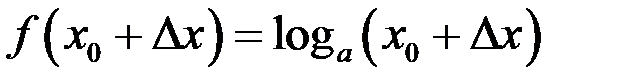 , то
, то 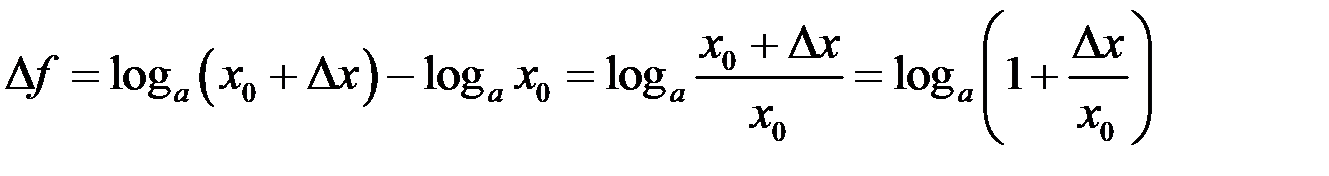 . Имеем
. Имеем 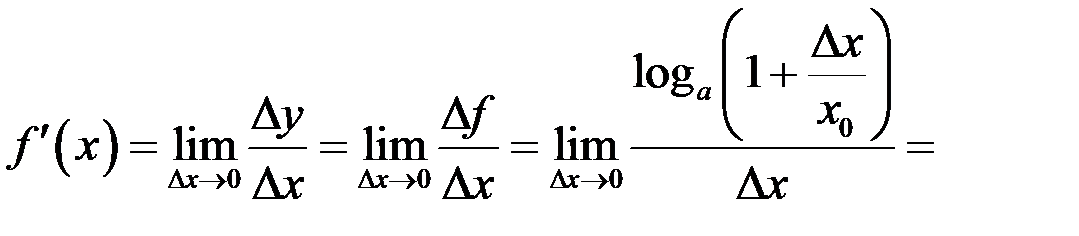
 .
.
Здесь мы использовали следствие из второго замечательного предела 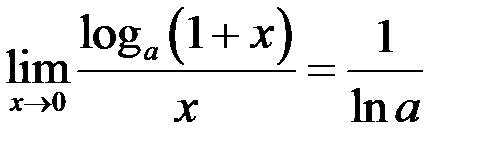 . В результате имеем
. В результате имеем  .
.
Пример 7. 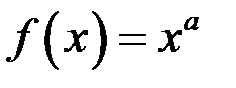 ,
, 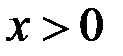 .
.
Так как 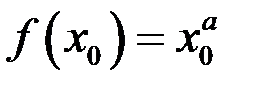 и
и  , то
, то 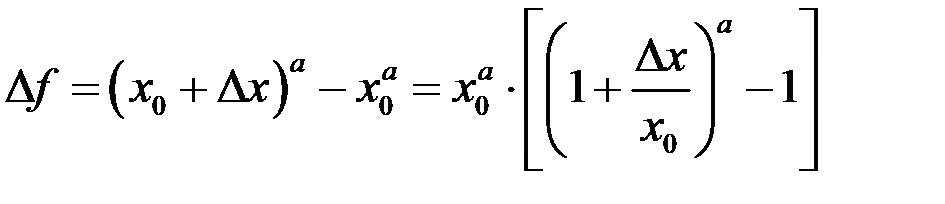 . Имеем
. Имеем

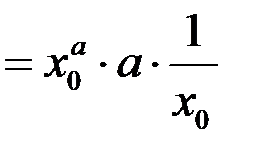 . Здесь мы использовали следствие из второго замечательного предела
. Здесь мы использовали следствие из второго замечательного предела 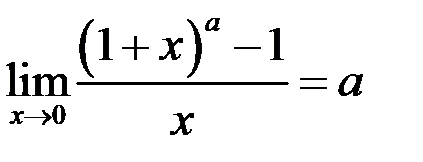 . То есть
. То есть 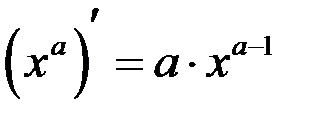 .
.
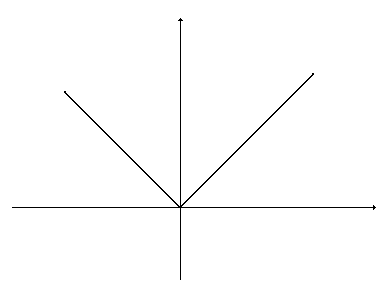
Пример 8.  ,
, 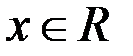 (рис. 9).
(рис. 9).
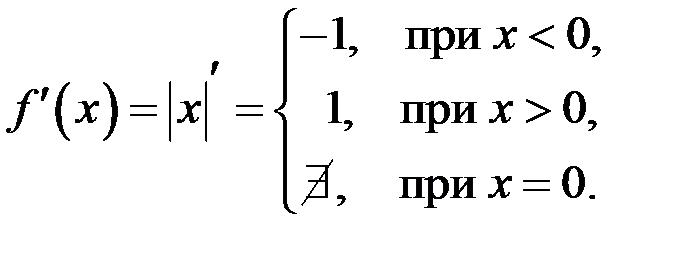 .
.
Заметим, что функция 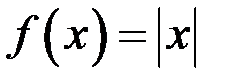 непрерывна, а её производная разрывна – свойства функции ухудшаются.
непрерывна, а её производная разрывна – свойства функции ухудшаются.
 Теорема (о производной обратной функции). Пусть функция
Теорема (о производной обратной функции). Пусть функция 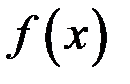 :
:
1) Определена на отрезке 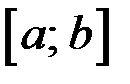 .
.
2) Строго монотонна на 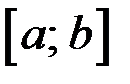 .
.
3) Непрерывна на 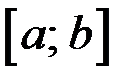 .
.
(Это условия теоремы о
существовании обратной функции),
Рис. 9 – График функции 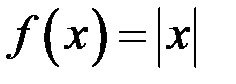 еще добавим
еще добавим
4) В точке 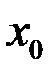 функция имеет производную, не равную нулю:
функция имеет производную, не равную нулю:  .
.
Тогда для обратной функции 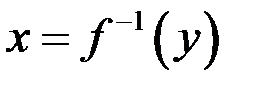 в соответствующей точке
в соответствующей точке 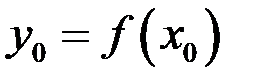 также существует производная
также существует производная  . (Другими словами
. (Другими словами 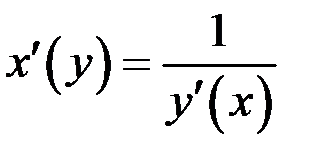 ).
).
Доказательство. Выполнение условий 1) – 3) позволяет сделать вывод (по теореме о существовании обратной функции) что существует обратная функция 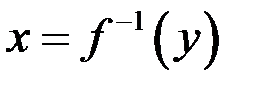 , непрерывная и однозначная на области значений функции
, непрерывная и однозначная на области значений функции  :
: 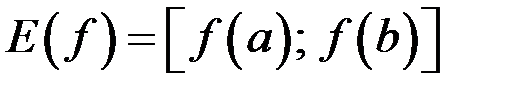 (если
(если  возрастает).
возрастает).
Обозначим 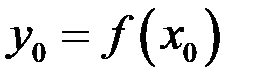 и придадим приращение аргументу
и придадим приращение аргументу  , тогда будем иметь приращение функции
, тогда будем иметь приращение функции 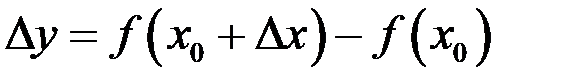 . Заметим, что, так как функция
. Заметим, что, так как функция 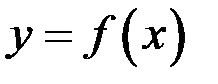 осуществляет взаимно однозначное отображение, то, как только
осуществляет взаимно однозначное отображение, то, как только 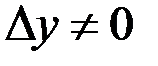 , так сразу
, так сразу 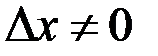 . А из непрерывности следует, что при
. А из непрерывности следует, что при 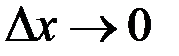
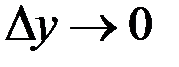 . Заметим, что
. Заметим, что 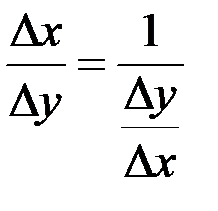 , следовательно
, следовательно
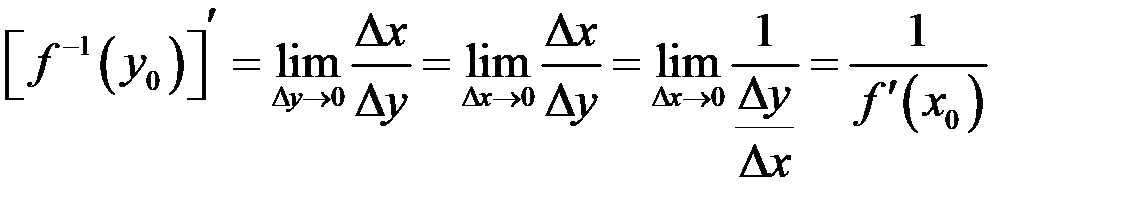 .
.
Используя эту теорему, найдем производные обратных тригонометрических функций.
Пример 1. Пусть 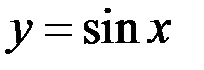 . Функция на
. Функция на 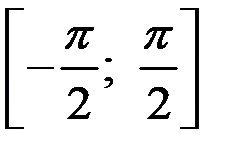 монотонна. Тогда существует обратная функция
монотонна. Тогда существует обратная функция 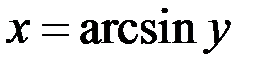 и
и 
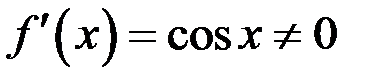 на
на 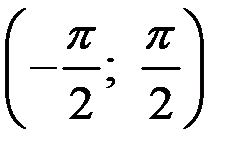 . Выполнены все условия теоремы о существовании производной обратной функции
. Выполнены все условия теоремы о существовании производной обратной функции
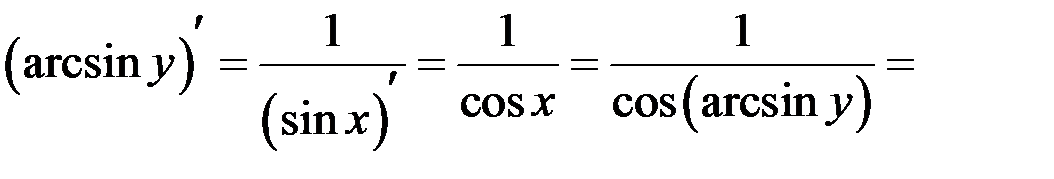
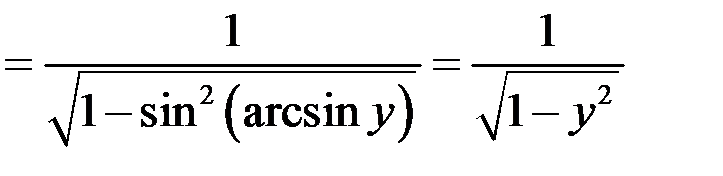 .
.
Пример 2. Пусть  . Функция на отрезке
. Функция на отрезке 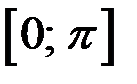 монотонна. Тогда существует обратная функция
монотонна. Тогда существует обратная функция  и существует
и существует  на
на  . Выполнены все условия теоремы о существовании производной обратной функции
. Выполнены все условия теоремы о существовании производной обратной функции

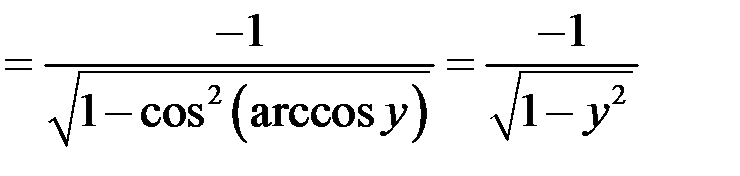 .
.
Пример 3. Пусть 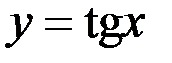 . Функция на
. Функция на 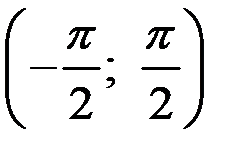 монотонна. Тогда существует обратная функция
монотонна. Тогда существует обратная функция 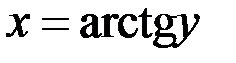 и существует
и существует 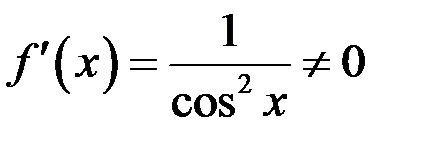 на
на 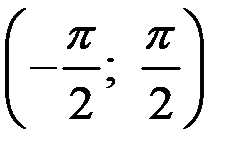 .
.
Выполнены все условия теоремы о существовании производной обратной функции
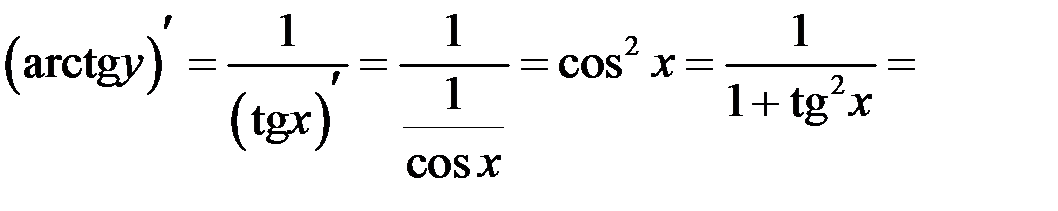
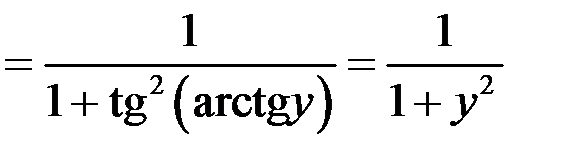 .
.
Гиперболические функции
Так называются функции
 ,
, 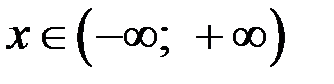 ;
;
 ,
,  ;
;
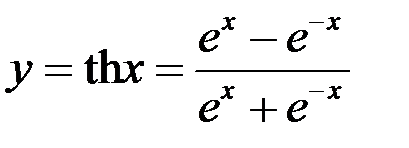 ,
, 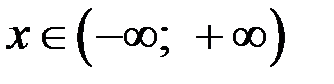 ;
;
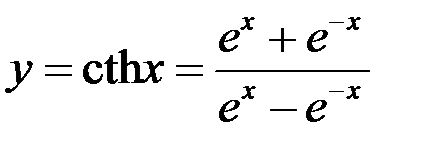 ,
, 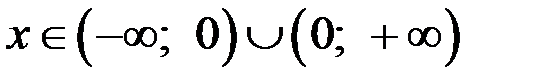 .
.
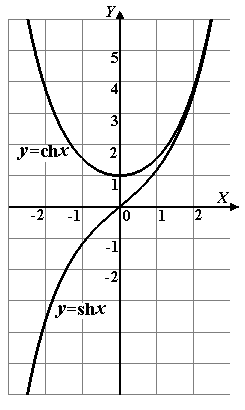
Эти функции названы по аналогии с тригонометрическими функциями (рис. 10 и 11). Имеют место формулы (обратить внимание на знаки!)
Соотношения между функциями одного аргумента
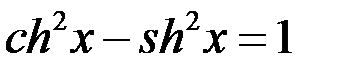 ;
; 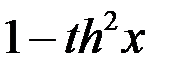 =
= 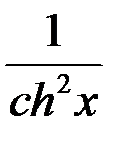 ;
;
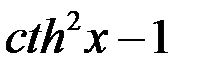 =
= 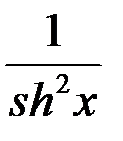 .
.
Рис. 10 – Гиперболические синус
и косинус
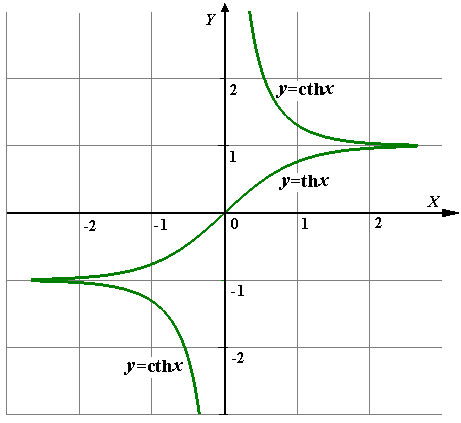 Формулы сложения
Формулы сложения
 =
= 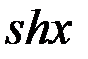
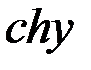
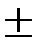
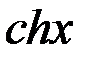
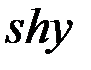 ;
;
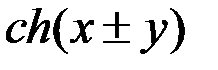 =
= 
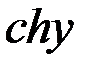

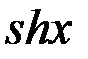
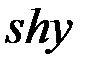 ;
;
 =
= 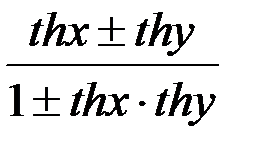 .
.
Формулы двойного аргумента
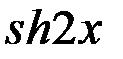 =2
=2 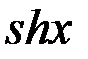
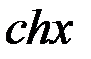 ;
;
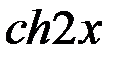 =
= 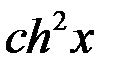 +
+ 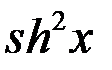 =2
=2 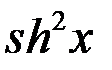 +1=2
+1=2  ;
;
 =
= 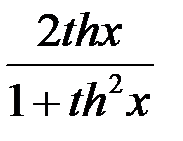 .
.
Формулы понижения степени
Рис. 11 – Гиперболические тангенс 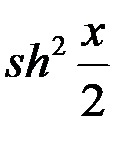 =
=  (
( 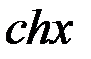 -1);
-1); 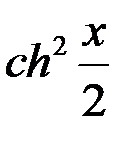 =
= 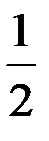 (
( 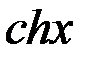 +1);
+1);
и котангенс 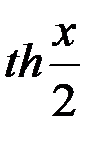 =
= 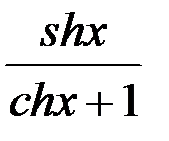 =
=  .
.
Формулы суммы
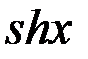
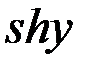 =2
=2 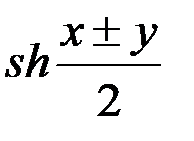
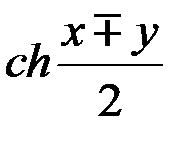 ;
;  +
+ 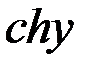 =2
=2 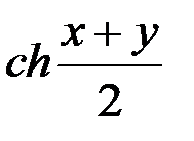
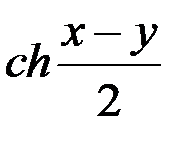 ;
;
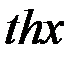
 =
= 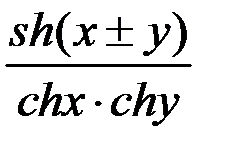 .
.
Формулы произведения
2 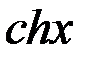
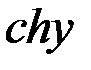 =
= 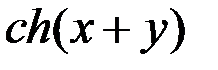 +
+ 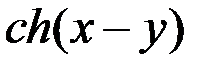 ; 2
; 2 
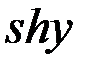 =
= 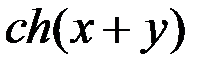 -
- 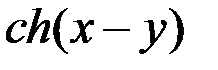 ;
;
2 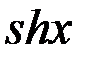
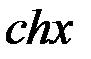 =
= 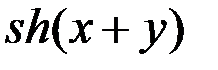 +
+ 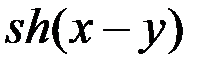 .
.
Формулы половинного аргумента
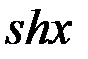 =
= 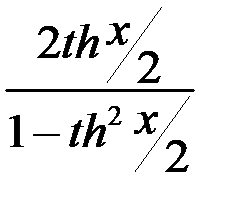 ;
;  =
= 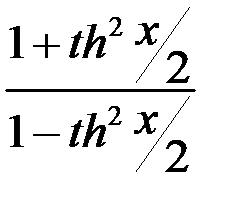 ;
; 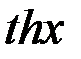 =
= 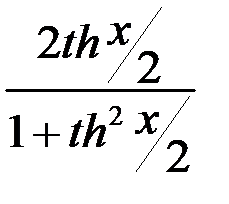 .
.
Эти тождества легко проверяются, если воспользоваться определениями функций через экспоненту 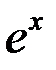 .
.
Таблица производных
| № | Исходная функция | Производная функция | Дифференциал 
|
| 1 | C | 0 | 0 |
| 2 | 
| 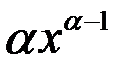
| 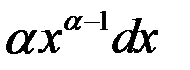
|
| 3 | 
| 
|  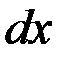
|
| 4 | 
| 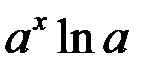
| 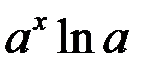 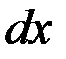
|
| 5 | 
| 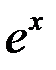
| 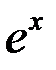 
|
| 6 | 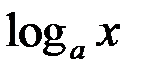
| 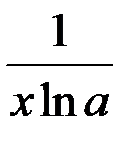
| 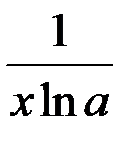 
|
| 7 | 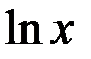
| 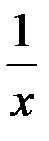
|  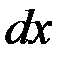
|
| 8 | 
| 
| 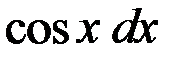
|
| 9 | 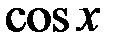
| 
| 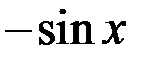 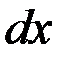
|
| 10 | 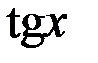
| 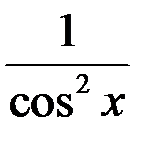
| 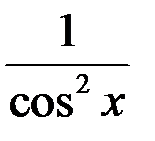 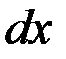
|
| 11 | 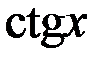
| 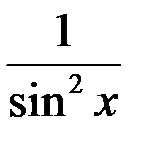
| 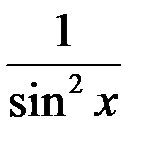 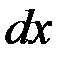
|
| 12 | 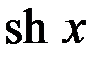
| 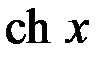
| 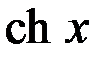 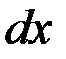
|
| 13 | 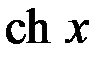
| 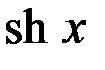
| 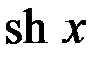 
|
| 14 | 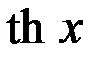
| 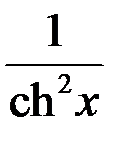
| 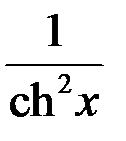 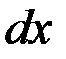
|
| 15 | 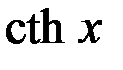
| 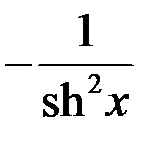
| 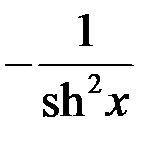 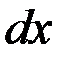
|
| 16 | 
| 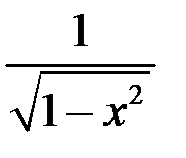
|  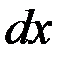
|
| 17 | 
| 
| 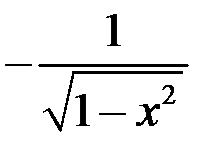 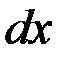
|
| 18 | 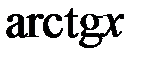
| 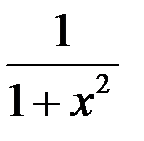
| 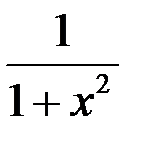 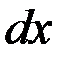
|
| 19 | 
| 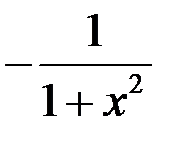
| 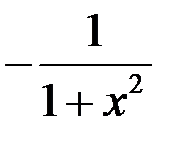 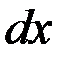
|
Дата: 2018-11-18, просмотров: 600.