Свойство 1. Если функция имеет предел 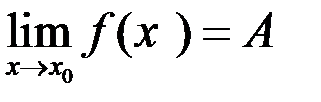 , то существует окрестность точки
, то существует окрестность точки 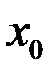 , в которой функция ограничена. (Это свойство можно назвать необходимым условием ограниченности функции, имеющей предел).
, в которой функция ограничена. (Это свойство можно назвать необходимым условием ограниченности функции, имеющей предел).
Свойство 2. Если 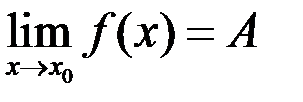
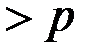 , то
, то 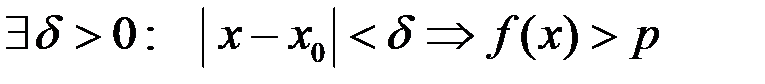 .
.
Замечание. Справедливо аналогичное свойство и в случае, если 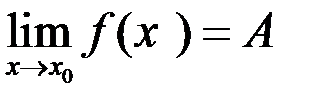
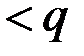 .
.
Свойство 3. (отделимость от нуля). Если 
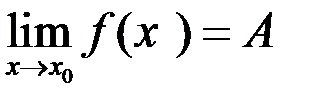
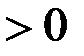 , то
, то 
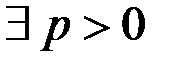
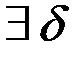
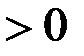 такие, что
такие, что 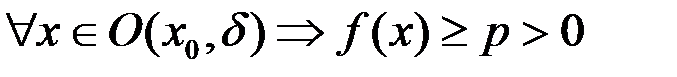 .
.
Свойство 4. (о единственности предела). Если функция имеет предел в точке 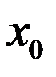 , то этот предел – единственный.
, то этот предел – единственный.
Свойства, связанные с арифметическими операциями над пределами
Пусть существуют конечные 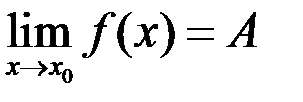 и
и 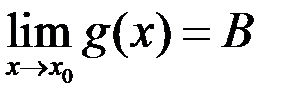 , тогда
, тогда
Свойство 5. Предел суммы двух функций равен сумме пределов.
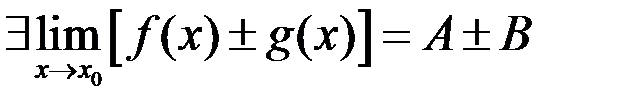 .
.
Свойство 6. Предел произведения двух функций равен произведению пределов.
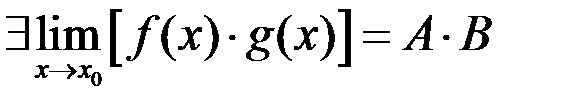 .
.
Свойство 7. Предел отношения двух функций равен отношению пределов.
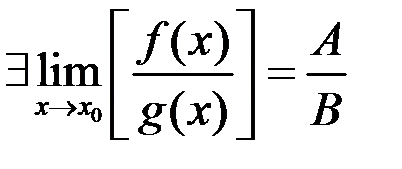 (при условии
(при условии 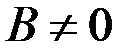 ).
).
Свойство 8. Предел произведения числа на функцию равен произведению числа на предел функции.
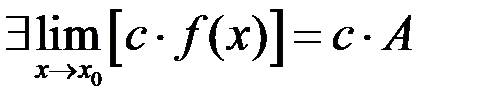 .
.
Свойства, связанные с предельными переходами в неравенствах
Свойство 9. (теорема о предельном переходе в неравенстве). Если в некоторой окрестности точки 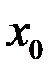 (
( 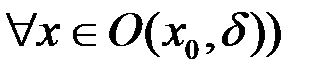 ) выполнено
) выполнено 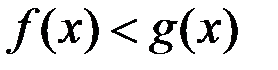 и существуют
и существуют 
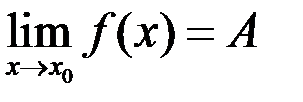 и
и 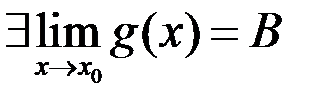 , то
, то 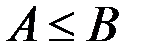 .
.
Замечание. При предельном переходе может возникнуть знак равенства.
Свойство 10. (теорема о пределе промежуточной функции, или о двух милиционерах). Если в некоторой окрестности точки 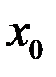
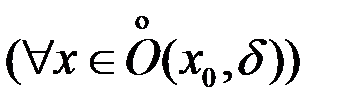 выполнено
выполнено 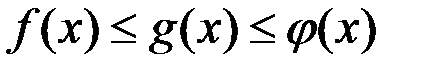 и существуют
и существуют
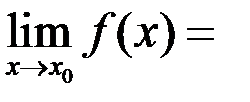
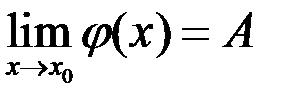 , то
, то 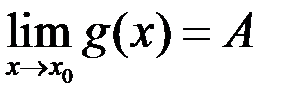 .
.
Аналогия между сходящимися последовательностями и функциями, имеющими пределы, распространяется и на критерий Коши.
Определение. Говорят, что функция 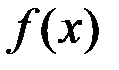 в точке
в точке 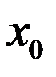 имеет «Ф-свойство» (по аналогии с фундаментальной последовательностью), если
имеет «Ф-свойство» (по аналогии с фундаментальной последовательностью), если 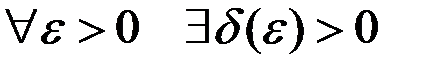 такое, что
такое, что
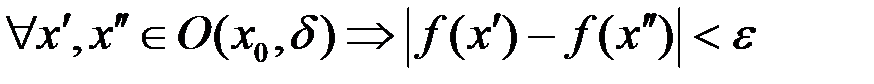 .
.
Критерий Коши. Для того, чтобы функция в точке имела конечный предел, необходимо и достаточно, чтобы она имела «Ф - свойство».
Вычисления пределов. Неопределенности
Определение. Число 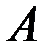 называется пределом функции
называется пределом функции 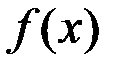 при
при 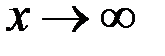 , если
, если 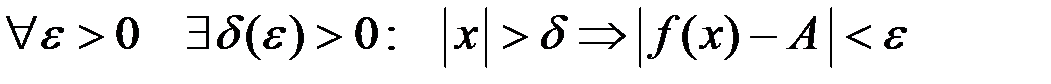 .
.
Аналогично односторонний предел можно определить как при 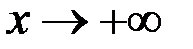 , так и при
, так и при 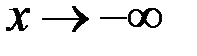 .
.
Замечание. Заметим, что свойства функций, имеющих предел, остаются справедливыми и в случае 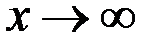 , если под окрестностью бесконечно удаленной точки будем понимать
, если под окрестностью бесконечно удаленной точки будем понимать 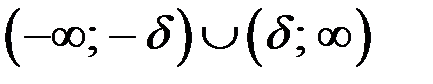 .
.
При вычислении пределов пользуются свойствами, связанными с арифметическими операциями над пределами.
Пример 1. 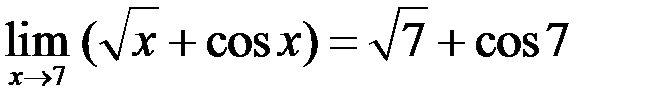 ;
;
Пример 2. 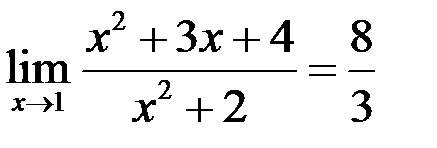 ;
;
Пример 3. 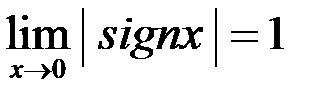 ;
;
Пример 4. 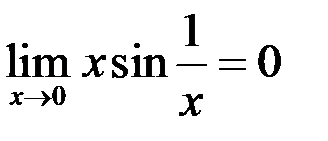 (б.м. умноженная на ограниченную).
(б.м. умноженная на ограниченную).
Поскольку мы добавили к 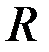 элементы
элементы 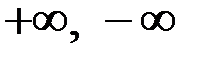 , то можно записать арифметические операции с этими элементами.
, то можно записать арифметические операции с этими элементами.
Так делают всегда, когда есть определенности.
Определенности
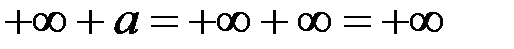 ;
; 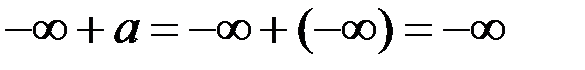 ;
;
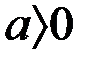
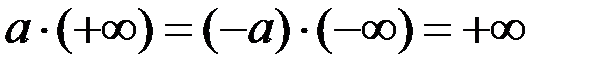 ;
; 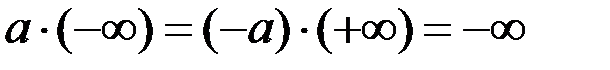 ;
;
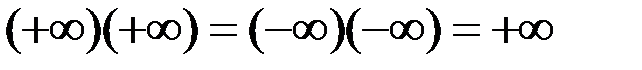 ;
; 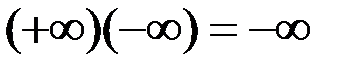 ;
;
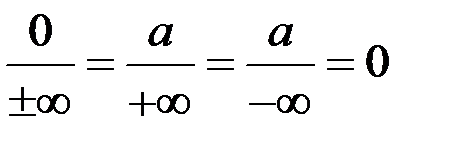 ; (
; ( 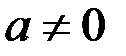 )
) 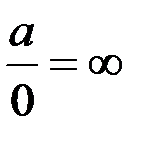 ;
; 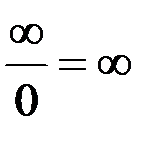 ;
;
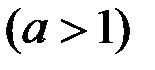
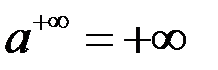 ;
; 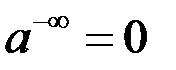 ;
;
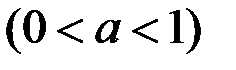
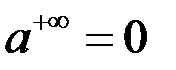 ;
; 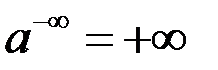 ;
;
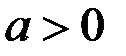
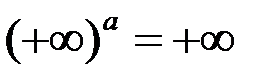 ;
; 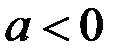
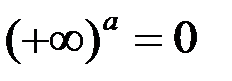 ;
;
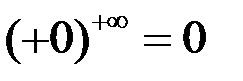 ;
; 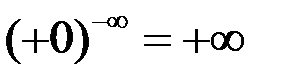 .
.
Есть особые случаи, когда предел суммы, произведения и частного нельзя найти, зная только пределы слагаемых, множителей или делимого и делителя. Такие случаи называются неопределенностями.
Неопределенности
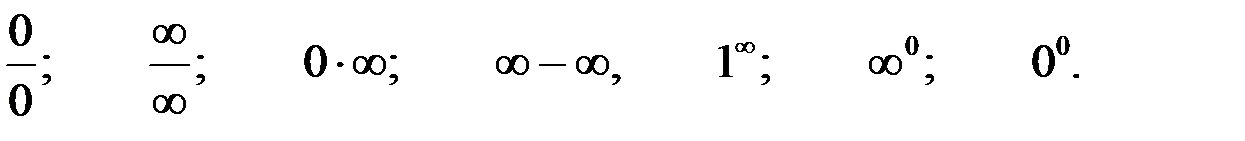
Пример. Предел рациональной дроби
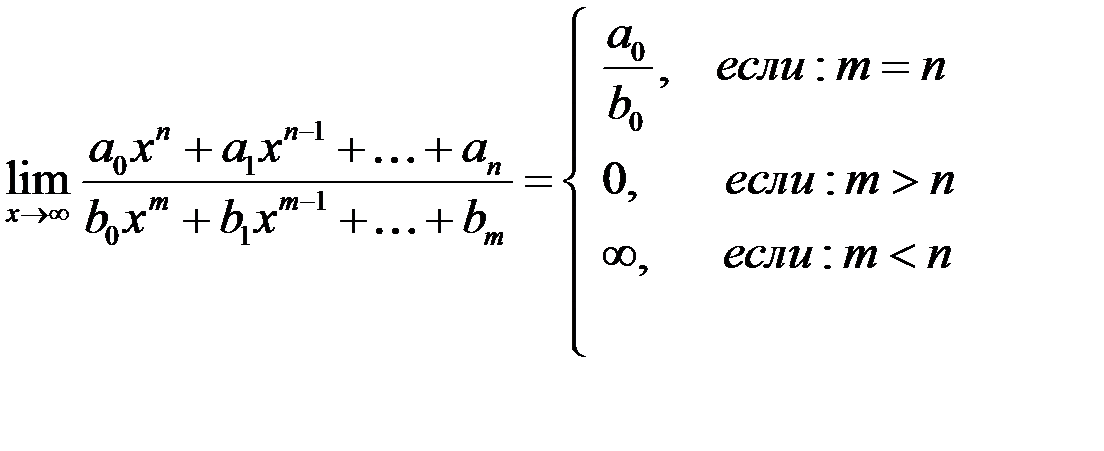 .
.
Замечательные пределы
Теорема (І замечательный предел). 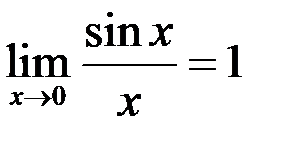
Замечание. Если в некоторой окрестности точки 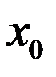 функция
функция 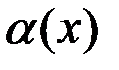 – б.м., то
– б.м., то 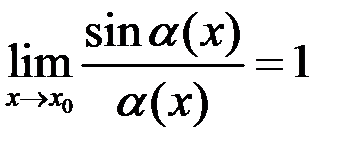 .
.
Теорема (ІІ замечательный предел). 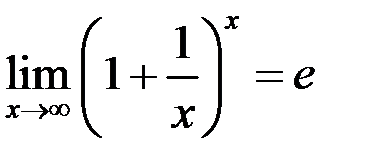
Следствие. Заменой 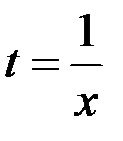 получим
получим 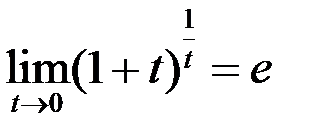 .
.
ІІІ 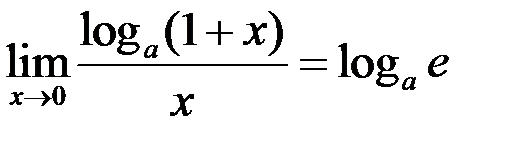 ;
; 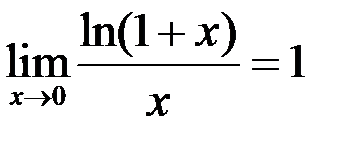 .
.
IV. 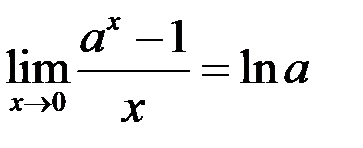 ;
; 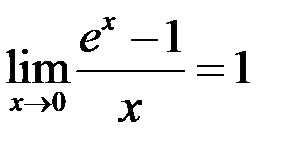 .
.
V. 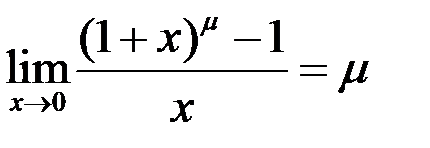 .
.
Замечание. Замечание к I пределу справедливо и для других.
Сравнение б.м. О-символика
Определение. Если для двух функций 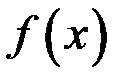 и
и 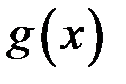 существует такая константа
существует такая константа 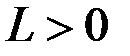 , что в некоторой окрестности точки
, что в некоторой окрестности точки 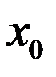 выполняется неравенство
выполняется неравенство 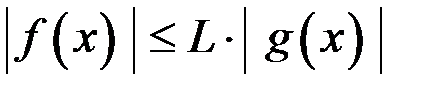 ,
, 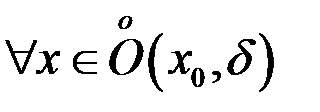 (то есть при
(то есть при 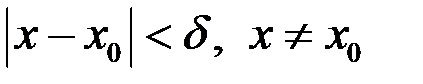 ), то говорят, что функция
), то говорят, что функция 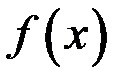 ограничена по сравнению с функцией
ограничена по сравнению с функцией 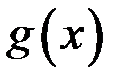 в некоторой окрестности точки
в некоторой окрестности точки 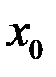 (или
(или 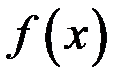 подчинена
подчинена 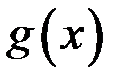 при
при 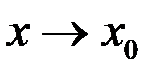 ). Обозначается
). Обозначается 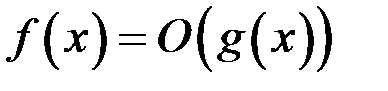 .
.
Определение. Если функции 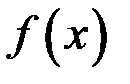 и
и 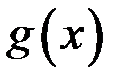 такие, что
такие, что 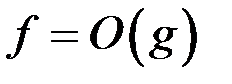 и
и 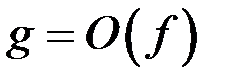 при
при 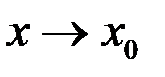 , то они называются функциями одного порядка при
, то они называются функциями одного порядка при 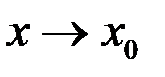 .
.
Определение. Говорят, что 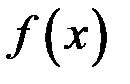 и
и 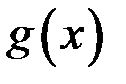 эквивалентны, если
эквивалентны, если 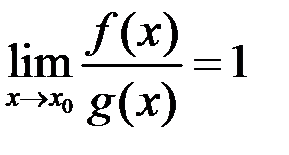 (при условии, что
(при условии, что 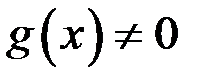 , в некоторой окрестности точки
, в некоторой окрестности точки 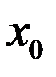 ). Обозначается
). Обозначается 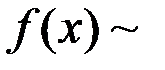
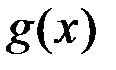 при
при 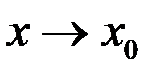 .
.
Определение. Если 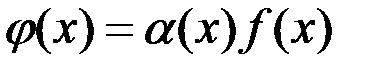 , где
, где 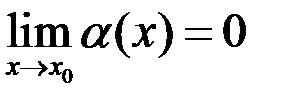 , то говорят, что
, то говорят, что 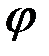 есть б.м. относительно функции
есть б.м. относительно функции 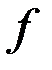 . Обозначается
. Обозначается 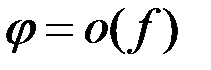 .
.
Определение. Говорят, что б.м. функция 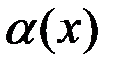 является величиной более высокого порядка малости, чем б.м.
является величиной более высокого порядка малости, чем б.м. 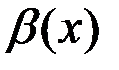 , если
, если
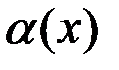
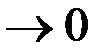 при
при 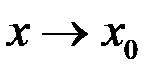 и
и 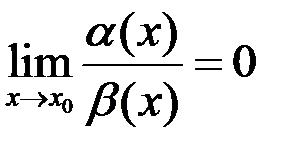 . Обозначается:
. Обозначается: 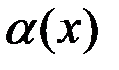 =
= 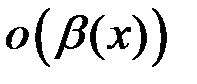 .
.
Определение. Говорят, что функции 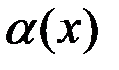 и
и 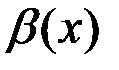 б.м. одного порядка малости, если существует конечный предел их отношения и он не равен нулю:
б.м. одного порядка малости, если существует конечный предел их отношения и он не равен нулю: 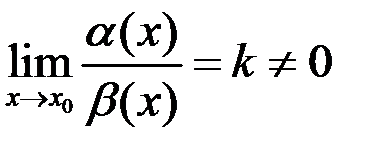 .
.
Теорема. Пусть 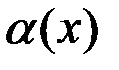 ~
~ 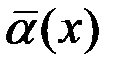 ,
, 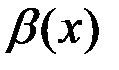 ~
~ 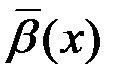 , при
, при 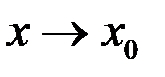 . Тогда
. Тогда 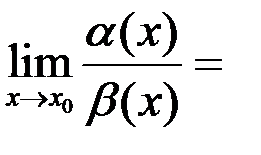
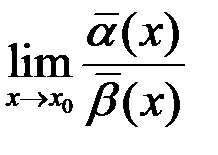 .
.
Теорема (об эквивалентных функциях). Функции 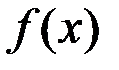 и
и 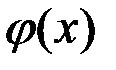 эквивалентны при
эквивалентны при 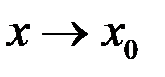 , если
, если 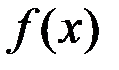 можно представить в виде:
можно представить в виде: 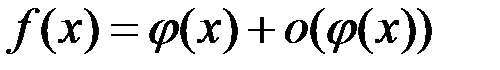 . При этом
. При этом 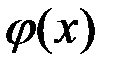 называют главной частью функции
называют главной частью функции 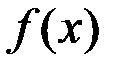 .
.
Таблица эквивалентных функций при 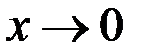
1. 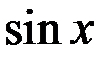 ~
~ 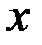 . 2.
. 2. 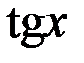 ~
~ 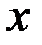 . 3.
. 3. 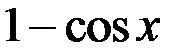 ~
~ 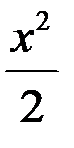 .
.
4. 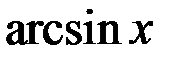 ~
~ 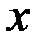 . 5.
. 5. 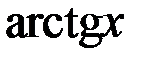 ~
~ 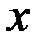 . 6.
. 6. 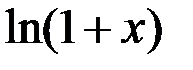 ~
~ 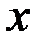 .
.
7. 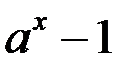 ~
~ 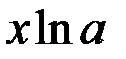 . 8.
. 8. 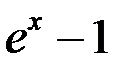 ~
~ 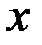 . 9.
. 9. 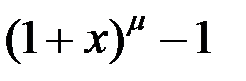 ~
~ 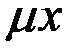 .
.
10. 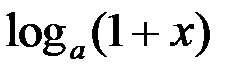 ~
~ 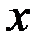
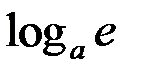 .
.
Правила действия с символом «О-большое» при 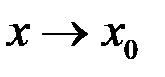
1. 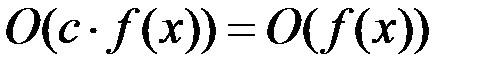 ,
, 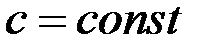 .
.
2. 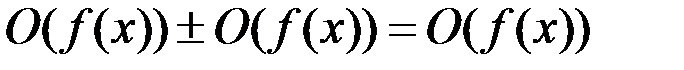 .
.
3. 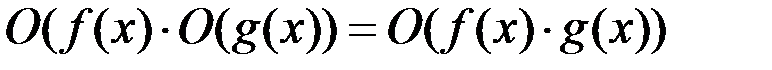 .
.
4. 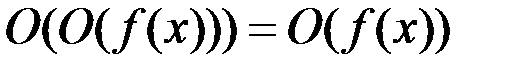 .
.
5. 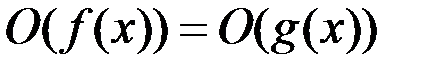 если
если 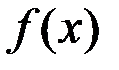 ~
~ 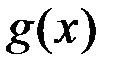 .
.
Правила действия с символом «о-малое» при 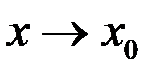
1. 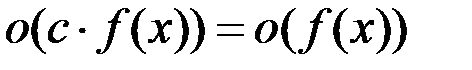 ,
, 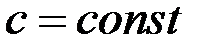 .
.
2. 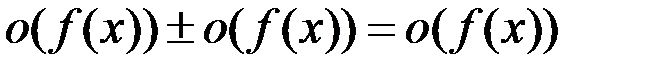 .
.
3. 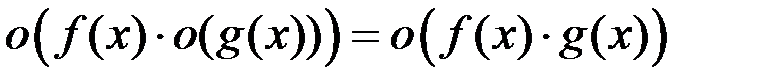 .
.
4. 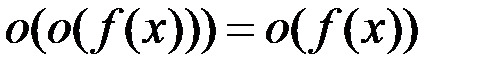 .
.
5. 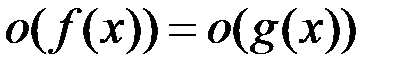 если
если 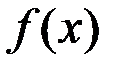 ~
~ 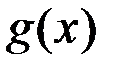 .
.
6. 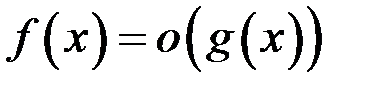
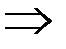
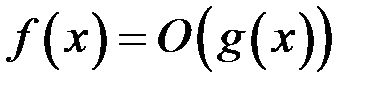 .
.
7. 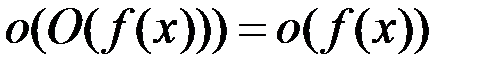 и
и 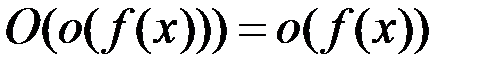 .
.
Замечание. Равенства 2–4 читаются слева направо.
Дата: 2018-11-18, просмотров: 755.