Следствие 1 (условие постоянства функции). Если 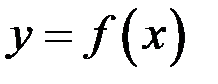 дифференцируема на
дифференцируема на 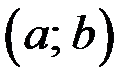 и
и 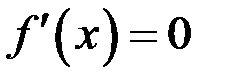
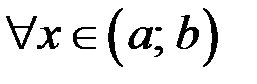 , то
, то 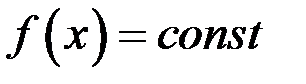 на
на 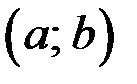 .
.
Следствие 2 (условие монотонности функции). Если  дифференцируема на
дифференцируема на 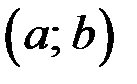 и
и 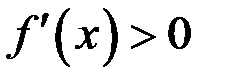 на
на 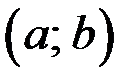 , то
, то 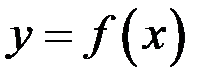 монотонно возрастает на
монотонно возрастает на 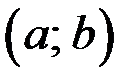 .
.
Следствие 3 (достаточное условие равномерной непрерывности функции). Если 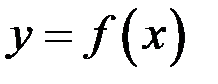 определена и имеет ограниченную производную на
определена и имеет ограниченную производную на 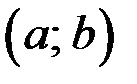 , то
, то 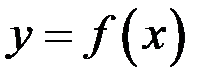 равномерно непрерывна на
равномерно непрерывна на 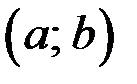 .
.
Пример. При каких значениях  функция
функция 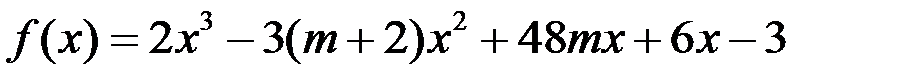 возрастает на всей числовой прямой.
возрастает на всей числовой прямой.
Решение. Область определения функции – вся числовая ось.
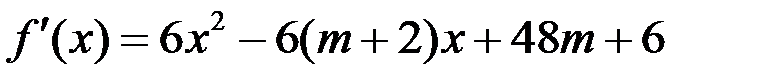
Функция 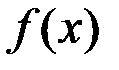 будет возрастающей на всей числовой прямой, если
будет возрастающей на всей числовой прямой, если 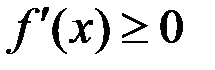 для всех
для всех 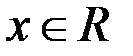
Отсюда: 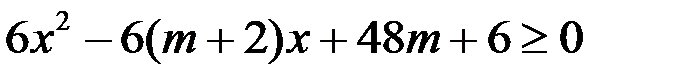
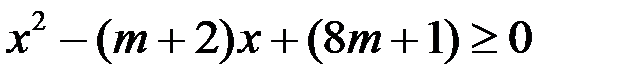
По свойству квадратного трёхчлена, он всегда неотрицателен, если 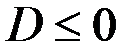 . Так как
. Так как 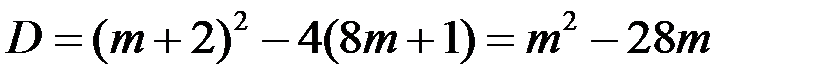 , то должно выполняться
, то должно выполняться 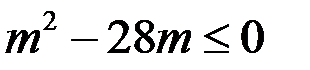 .
.
Решением данного неравенства является отрезок 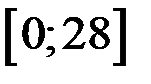 .
.
Следовательно, данная функция 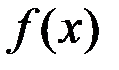 возрастает на всей числовой прямой при
возрастает на всей числовой прямой при 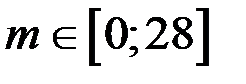 .
.
Теорема Коши. Пусть функции 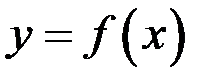 и
и 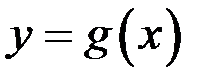 :
:
1. Непрерывны на отрезке 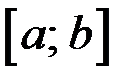 ,
,
2. Имеют в каждой точке интервала  производные
производные 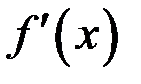 и
и 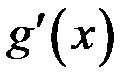 ,
,
3. 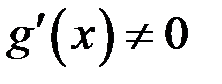 во всех точках интервала
во всех точках интервала 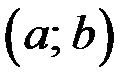 .
.
Тогда существует точка 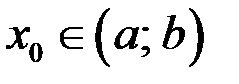 такая, что
такая, что 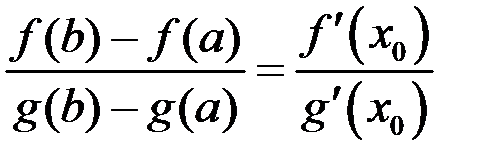 .
.
Следствие из теоремы Коши. Если 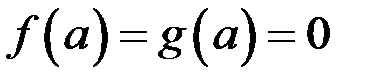 , то
, то 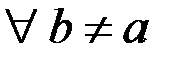
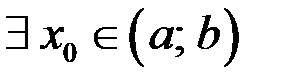 такая, что
такая, что 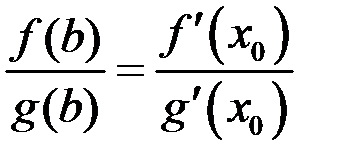 .
.
Задачи для самостоятельного решения
1. Доказать, что производная дифференцируемой четной функции есть нечетная функция.
2. Привести пример дифференцируемой функции. которая является нечетной, но ее производная – четная функция.
3. Привести пример двух функций, каждая из которых не имеет производной в точке 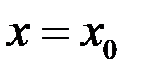 , и таких что:
, и таких что:
1) 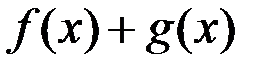 , дифференцируема в точке
, дифференцируема в точке 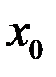 ;
;
2) 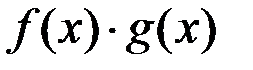 , дифференцируема в точке
, дифференцируема в точке 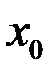 ;
;
4. Доказать, что производная дифференцируемой периодической функции есть функция, периодическая с таким же периодом.
5. Доказать, что если производная дифференцируемой функции 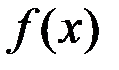 есть нечетная функция, то функция
есть нечетная функция, то функция 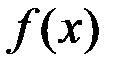 – четная.
– четная.
6. Привести пример двух функций, каждая из которых не имеет производной в точках 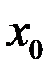 и
и 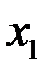 , и таких, что их произведение дифференцируемо в точках
, и таких, что их произведение дифференцируемо в точках 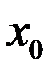 и
и 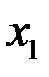 .
.
Контрольные вопросы и задания
В этом разделе представлены образец контрольной работы и экзаменационные вопросы по данной теме в помощь студентам с целью плановой и более качественной подготовки к контрольным мероприятиям. Также представлен список учебной литературы по данной теме.
Образцы контрольной работы
Вариант 1
1. Записать на языке 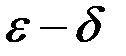 и нарисовать эскиз графика: а)
и нарисовать эскиз графика: а) 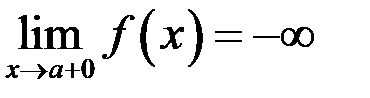 ; б)
; б) 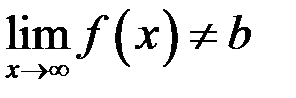 .
.
2. Исследовать на непрерывность и указать характер точек разрыва;
а) 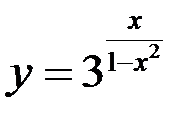 ; б)
; б) 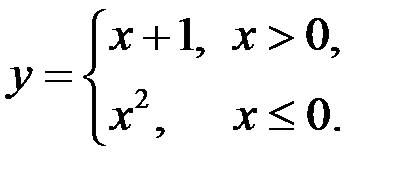 .
.
3. Найти пределы: а) 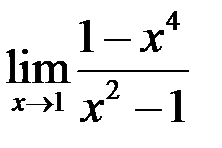 ; б)
; б) 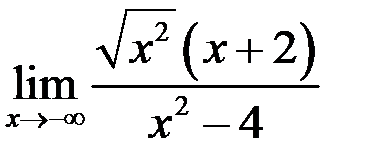 ; в)
; в) 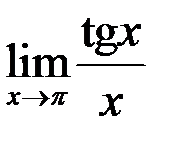 ; г)
; г) 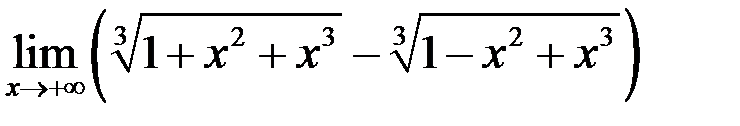 ; д)
; д) 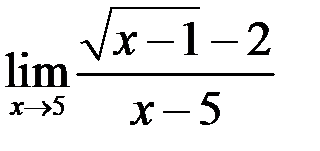 ; е)
; е) 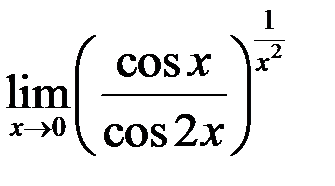 ; ж)
; ж) 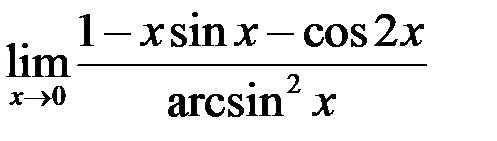 ; з)
; з) 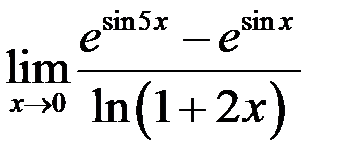 .
.
Вариант 2
1. Найти 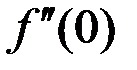 и
и 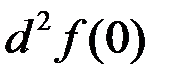 , если
, если 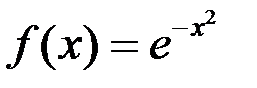 .
.
2. Найти 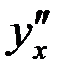 , если
, если 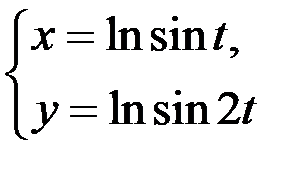 .
.
3. В каких точках касательные к кривой 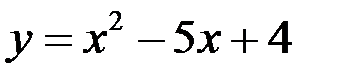 параллельны прямой
параллельны прямой 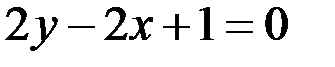 .
.
4. Составить уравнение касательной к кривой 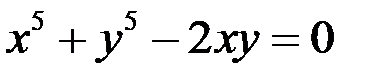 в точке (1;1).
в точке (1;1).
5. Найти угол наклона касательной к кривой 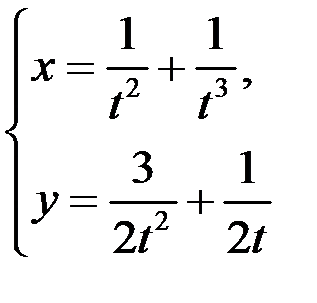 в точке
в точке 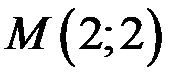 .
.
6. Написать уравнение нормали к кривой, заданной параметрически 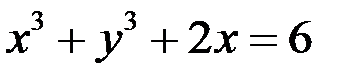 в точке
в точке 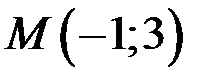 .
.
7. Найти производные функций: а) 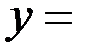
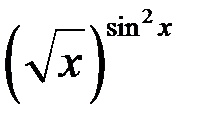 ; б)
; б) 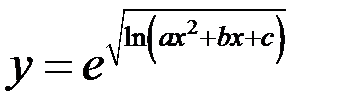 ; в)
; в) 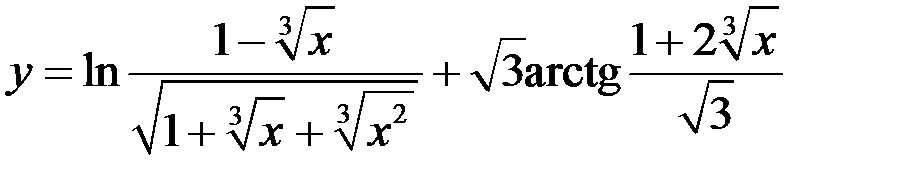 ; г)
; г) 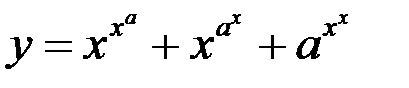 .
.
Экзаменационные вопросы по данной теме
Дата: 2018-11-18, просмотров: 560.