 Теорема Ферма. (О необходимом условии экстремума дифференцируемой функции). Пусть
Теорема Ферма. (О необходимом условии экстремума дифференцируемой функции). Пусть 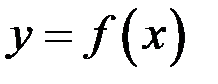 определена на некотором интервале
определена на некотором интервале 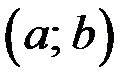 и в точке
и в точке 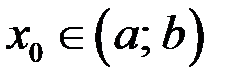 принимает наибольшее или наименьшее значение на
принимает наибольшее или наименьшее значение на 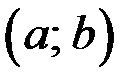 . Тогда если
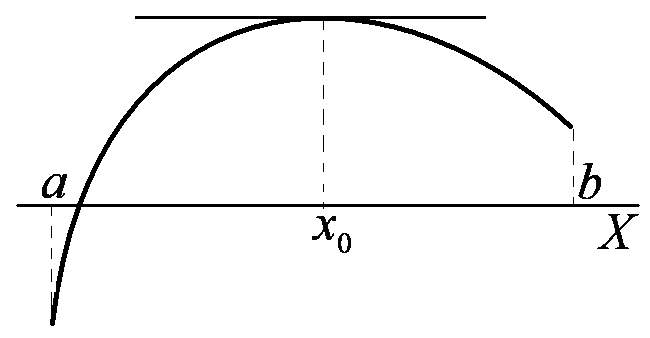
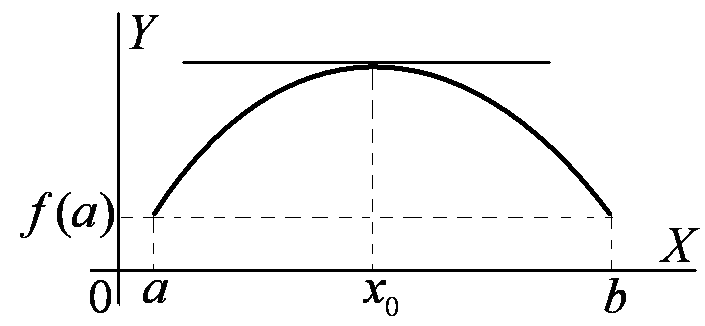
. Тогда если 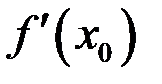 Рис. 16 – Теорема Ферма существует, то она равна нулю (рис. 16).
Рис. 16 – Теорема Ферма существует, то она равна нулю (рис. 16).
Доказательство. Пусть для определенности функция 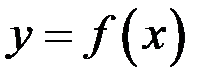 в точке
в точке 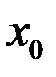 принимает наибольшее значение, то есть
принимает наибольшее значение, то есть 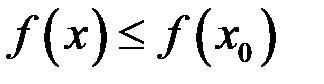 ,
, 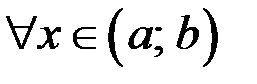 .
.
Тогда 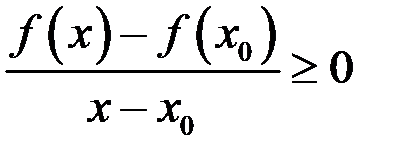 , если
, если 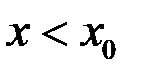 ;
;
и 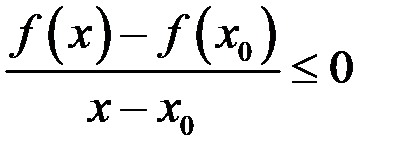 если
если 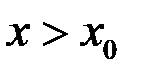 .
.
Если существует производная в точке 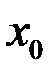 :
: 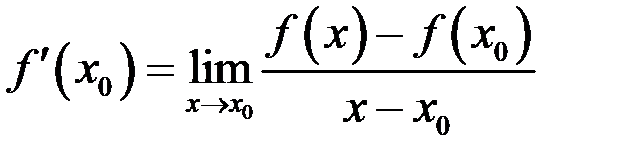 , то переходя к пределу при
, то переходя к пределу при 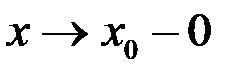 из первого неравенства получим, что
из первого неравенства получим, что 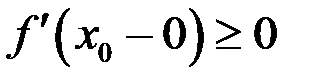 , а с другого неравенства при
, а с другого неравенства при 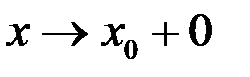 получим
получим 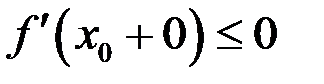 (неравенства становятся нестрогими по свойству 9 предельных переходов в неравенствах из §3 главы 3). Полученные неравенства приводят к двум вариантам: 1)
(неравенства становятся нестрогими по свойству 9 предельных переходов в неравенствах из §3 главы 3). Полученные неравенства приводят к двум вариантам: 1) 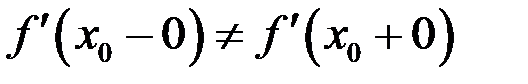 – производная не существует; 2)
– производная не существует; 2) 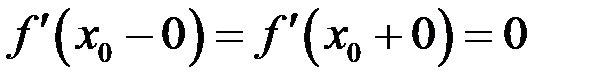 – производная существует и равна нулю.
– производная существует и равна нулю.
Геометрическая интерпретация. Если в точке 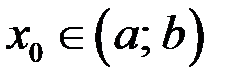 функция дифференцируема и принимает наибольшее или наименьшее значение, то касательная в точке
функция дифференцируема и принимает наибольшее или наименьшее значение, то касательная в точке 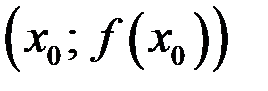 к графику функции параллельна оси
к графику функции параллельна оси 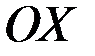 .
.
Замечание. Функция определена на интервале для того, чтобы она принимала наибольшее значение во внутренней точке, то есть, чтобы существовал двусторонняя окрестность, в которой 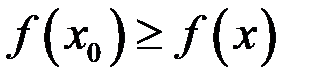 . В случае отрезка
. В случае отрезка 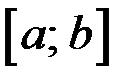
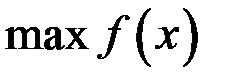 может достигаться на одном из концов и тогда для односторонней окрестности будут выполнены
может достигаться на одном из концов и тогда для односторонней окрестности будут выполнены 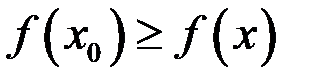 , но при этом односторонняя производная не обязана обращаться в ноль.
, но при этом односторонняя производная не обязана обращаться в ноль.
Теорема Ролля. Пусть функция 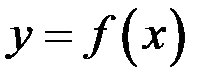 :
:
 1. Непрерывна на отрезке
1. Непрерывна на отрезке 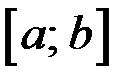 ,
,
2. Имеет в каждой точке интервала 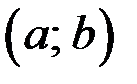 производную,
производную,
3. 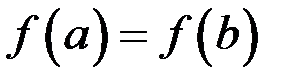 .
.
Тогда существует такая точка 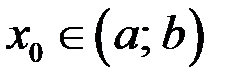 , Рис. 17 – Теорема Ролля что
, Рис. 17 – Теорема Ролля что 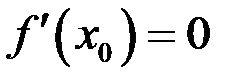 (рис. 17).
(рис. 17).
Доказательство. Так как непрерывна на отрезке, то по второй теореме Вейерштрасса найдутся точки 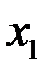 и
и 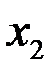 из
из 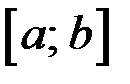 , в которых функция принимает наибольшее и наименьшее значения на
, в которых функция принимает наибольшее и наименьшее значения на 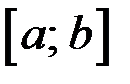 :
: 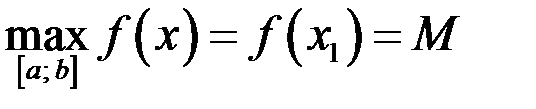 и
и 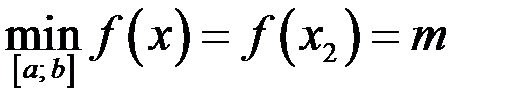 .
.
Тогда 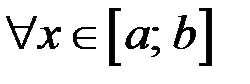 выполнено
выполнено 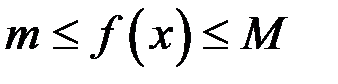 . Рассмотрим два случая.
. Рассмотрим два случая.
Случай 1. 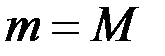 , тогда
, тогда 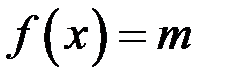
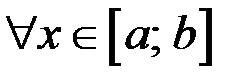
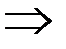 функция постоянна и ее производная
функция постоянна и ее производная 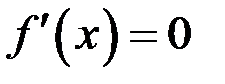 ,
, 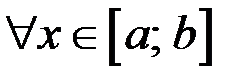 и в качестве
и в качестве 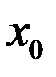 можно брать любую точку
можно брать любую точку 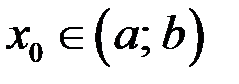 .
.
Случай 2. 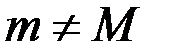 (
( 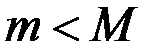 ), тогда из условия теоремы
), тогда из условия теоремы 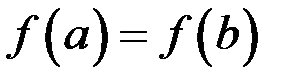 следует, что, хотя бы одна из точек
следует, что, хотя бы одна из точек 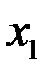 или
или 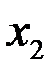 принадлежит интервалу
принадлежит интервалу 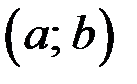 (внутренняя). Пусть это будет
(внутренняя). Пусть это будет 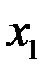 :
: 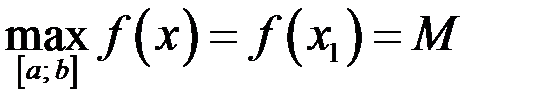 . То есть в точке
. То есть в точке 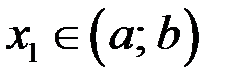 функция достигает
функция достигает 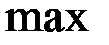 . По теореме Ферма
. По теореме Ферма 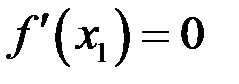 . Точка нашлась.
. Точка нашлась.
Геометрическая интерпретация. Если функция 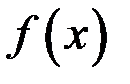 непрерывна и дифференцируема внутри отрезка и на концах принимает одинаковые значения то тогда внутри отрезка существует точка, в которой касательная параллельна оси
непрерывна и дифференцируема внутри отрезка и на концах принимает одинаковые значения то тогда внутри отрезка существует точка, в которой касательная параллельна оси 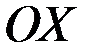 . Теорема не утверждает, что это единственная точка.
. Теорема не утверждает, что это единственная точка.
Задачи для самостоятельного решения
1. Доказать, что корни многочлена 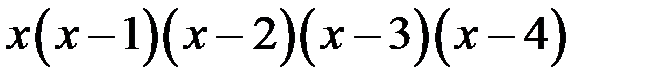 действительны, простые и принадлежат интервалам
действительны, простые и принадлежат интервалам 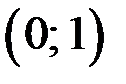 ;
; 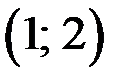 ;
; 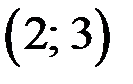 ;
; 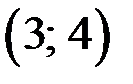 .
.
2. Доказать, что если функция 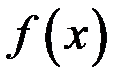 удовлетворяет условиям теоремы Ролля на отрезке
удовлетворяет условиям теоремы Ролля на отрезке 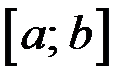 и не является постоянной, то на этом отрезке существуют такие точки
и не является постоянной, то на этом отрезке существуют такие точки 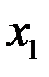 и
и 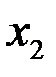 , что
, что 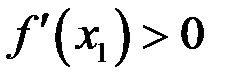 ,
, 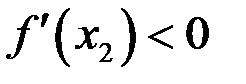 .
.
 Теорема Лагранжа (о среднем значении в дифференциальном исчислении). Пусть функция
Теорема Лагранжа (о среднем значении в дифференциальном исчислении). Пусть функция 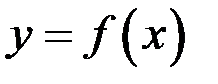 :
:
1. Непрерывна на отрезке 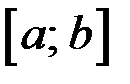 ,
,
2. Имеет в каждой точке интервала 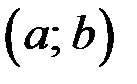 производную,
производную,
Тогда существует точка 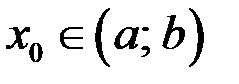 такая, что
такая, что 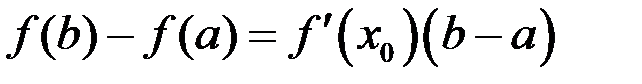 (рис. 18).
(рис. 18).
Рис. 18 – Теорема Лагранжа
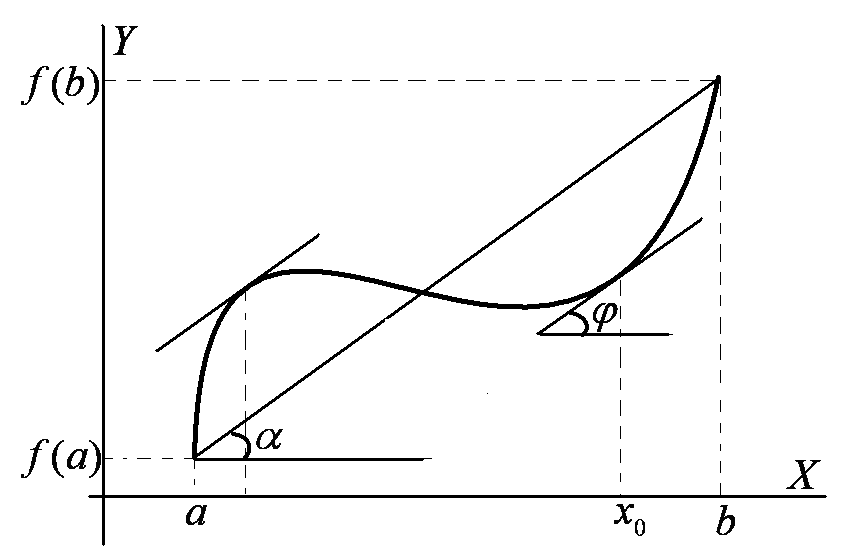
Геометрическая интерпретация. Если некоторая дуга кривой является графиком непрерывной и дифференцируемой функции, то на этой дуге найдется точка, в которой касательная наклонена к оси 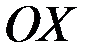 под таким же углом как и секущая
под таким же углом как и секущая 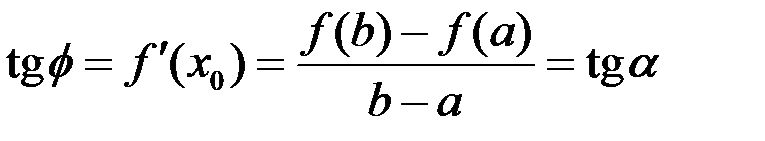
Дата: 2018-11-18, просмотров: 502.