Определение. Последовательность называется монотонно возрастающей, если 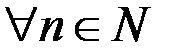
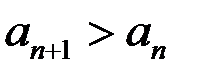 (строго возрастающей).
(строго возрастающей).
Аналогично: строго убывающая, если 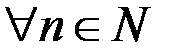
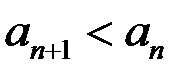 .
.
Если 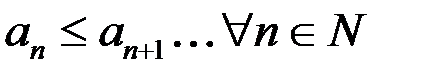 , то говорят, что последовательность неубывающая, а если
, то говорят, что последовательность неубывающая, а если 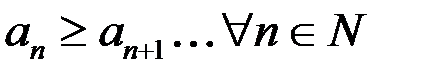 – что последовательность невозрастающая.
– что последовательность невозрастающая.
Пример. 1) 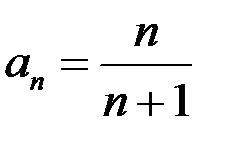 возрастает для любого
возрастает для любого 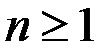 ;
;
2) 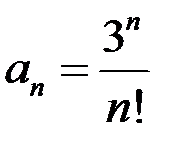 убывает для любого
убывает для любого 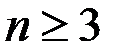 .
.
Теорема (Вейерштрасса). Если последовательность монотонна и ограничена, то она сходится.
Доказательство. Пусть 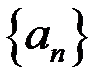 – возрастающая последовательность. Так как она ограничена, то
– возрастающая последовательность. Так как она ограничена, то 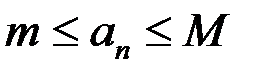 .
.
Тогда по теореме о существовании точной верхней грани существует 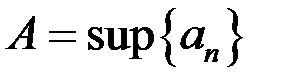 . Следовательно, выполняются два условия определения верхней грани:
. Следовательно, выполняются два условия определения верхней грани:
1) 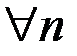
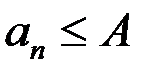 ;
;
2) 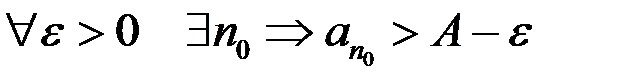 .
.
Так как 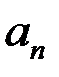 возрастающая, то
возрастающая, то 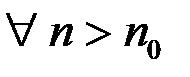 выполнено
выполнено 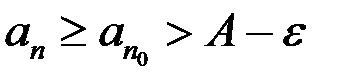 и имеем
и имеем 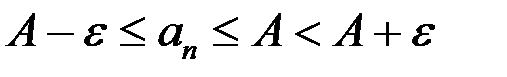 , или
, или 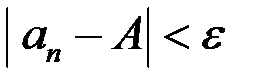 .
.
Замечание. Теорема справедлива, если последовательность монотонна, начиная с некоторого номера 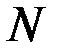 .
.
Пример. Доказательство существования числа 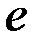 .
.
Решение. Рассмотрим последовательность 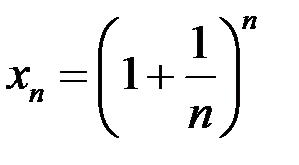 и покажем, что она монотонная и ограниченная, то есть, выполнены все условия теоремы Вейерштрасса. Проверим монотонность
и покажем, что она монотонная и ограниченная, то есть, выполнены все условия теоремы Вейерштрасса. Проверим монотонность
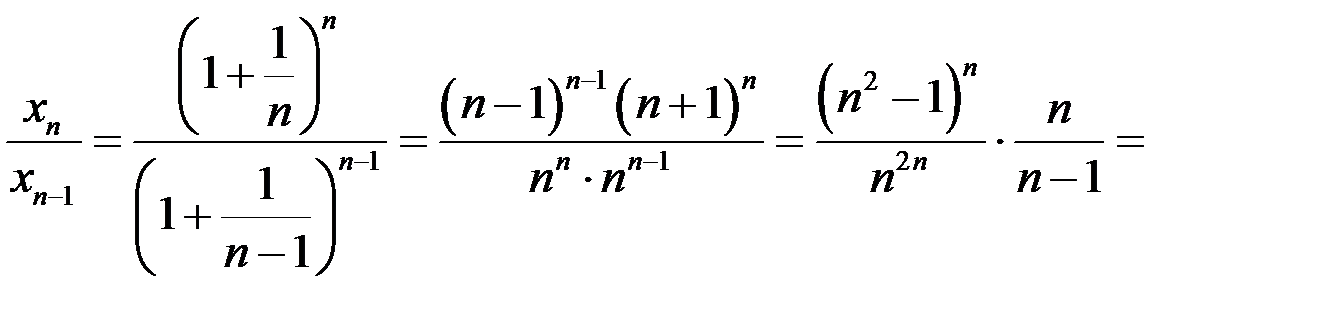
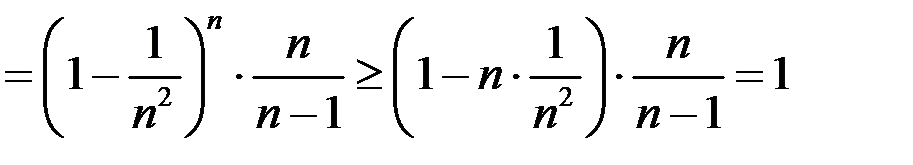 .
.
Мы применили неравенство Бернулли (Если 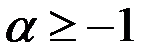 , то
, то 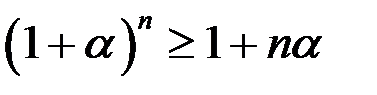 ), обозначив
), обозначив 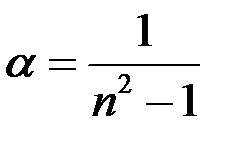 , при этом очевидно, что
, при этом очевидно, что 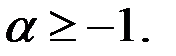
Проверим ограниченность, воспользовавшись формулой бинома Ньютона
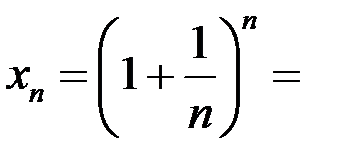
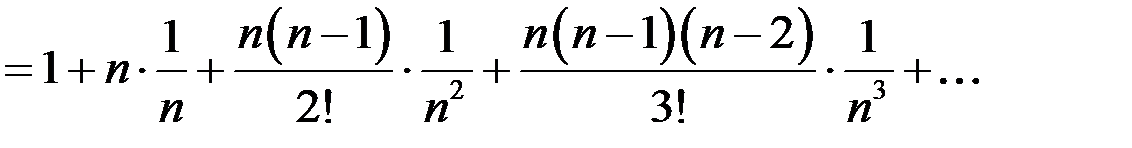
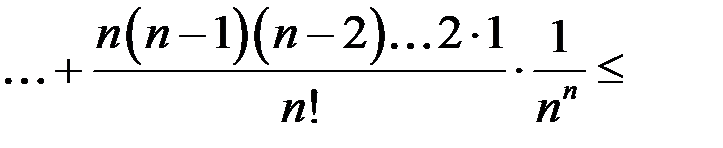
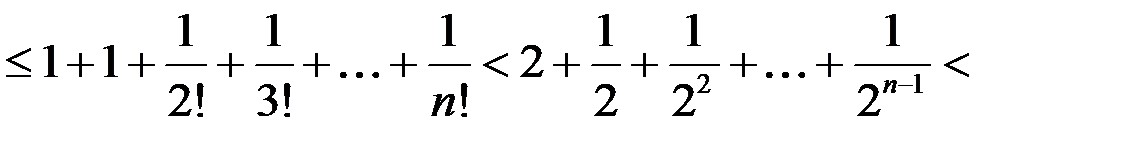
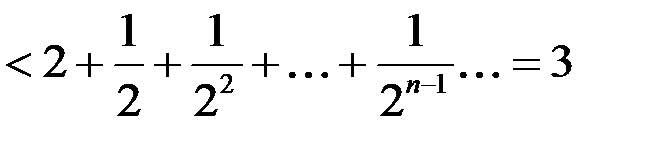 .
.
Последовательность 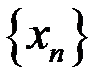 – неубывающая и ограниченная, а потому, по теореме Вейерштрасса, она сходящаяся и имеет конечный предел. Обозначают предел последовательности
– неубывающая и ограниченная, а потому, по теореме Вейерштрасса, она сходящаяся и имеет конечный предел. Обозначают предел последовательности 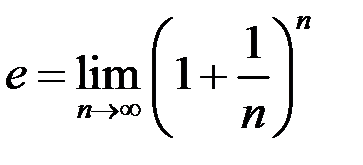 , а ее числовое значение
, а ее числовое значение 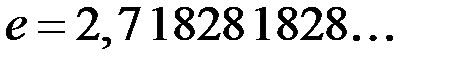
Подпоследовательность
Пусть имеется последовательность 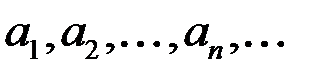 . Отметим каким-либо образом в ней бесконечно много членов и перенумеруем их заново слева направо. Получим набор
. Отметим каким-либо образом в ней бесконечно много членов и перенумеруем их заново слева направо. Получим набор 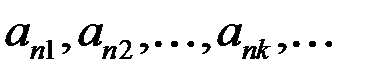 , который назовем подпоследовательностью.
, который назовем подпоследовательностью.
Определение. Если из данной последовательности выбрать бесконечное число членов с сохранением порядка, то получим подпоследовательность данной последовательности.
Теорема (о пределе подпоследовательности). Если последовательность имеет предел (конечный или нет), то такой же предел имеет и любая ее подпоследовательность.
Задача для самостоятельного решения
1. Для последовательности 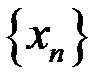 её подпоследовательности
её подпоследовательности 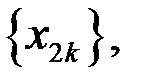
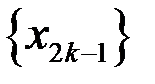 и
и 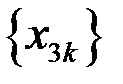 сходятся. Доказать, что сходится и сама последовательность.
сходятся. Доказать, что сходится и сама последовательность.
Теорема (Больцано – Вейерштрасса). Из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность.
Теорема. Из неограниченной последовательности можно извлечь б.б. подпоследовательность.
Определение. Предел любой сходящейся подпоследовательности называется частичным пределом данной последовательности.
Следствие. Теорема Больцано – Вейерштрасса утверждает, что всякая ограниченная последовательность имеет хотя бы один частичный предел.
Определение. Частичные пределы последовательности 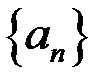 образуют множество предельных точек этой последовательности, которое имеет наибольший и наименьший элемент.
образуют множество предельных точек этой последовательности, которое имеет наибольший и наименьший элемент.
Задачи для самостоятельного решения
1. Доказать, что множество предельных точек последовательности 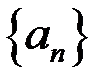 имеет наибольший и наименьший элемент. При этом их обозначают:
имеет наибольший и наименьший элемент. При этом их обозначают: 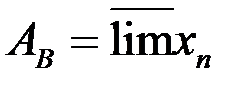 ,
, 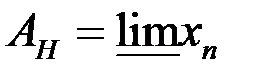 .
.
2. Доказать, что верхний и нижний пределы также являются предельными точками последовательности 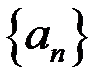 .
.
Проверка последовательности на сходимость не всегда целесообразна по определению. Это связано с тем, что в определении сходящейся последовательности участвует значение предела, которое может быть и неизвестным. Поэтому желательно иметь какой-нибудь критерий для определения сходимости или расходимости последовательности, основанный только на свойствах элементов данной последовательности. Сформулируем такой критерий.
Определение. Последовательность 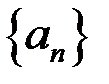 называется фундаментальной, если
называется фундаментальной, если 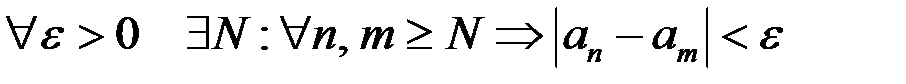 .
.
Теорема (Критерий Коши). Для того, чтобы последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.
Задачи для самостоятельного решения
1. Последовательность 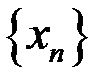 ограничена,
ограничена, 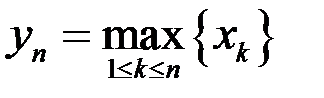 ,
, 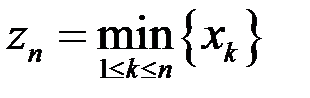 . Доказать, что последовательности
. Доказать, что последовательности 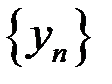 и
и 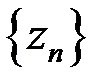 сходятся.
сходятся.
2. Пусть 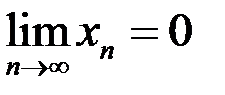 . Доказать, что
. Доказать, что 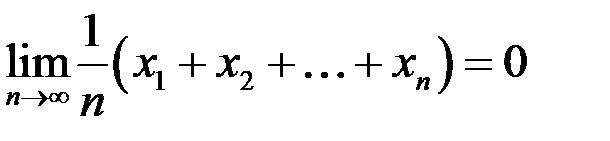 .
.
3. Пусть 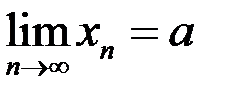 . Доказать, что
. Доказать, что 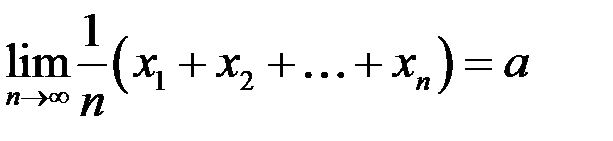 .
.
4. Привести пример сходящейся последовательности 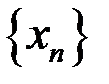 , для которой существует
, для которой существует 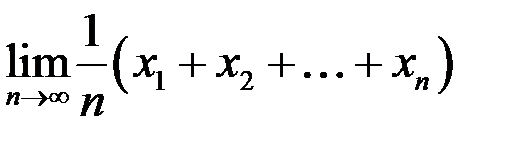 .
.
Значения некоторых пределов
1. 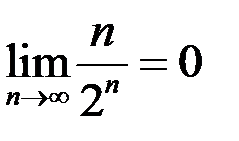 2.
2. 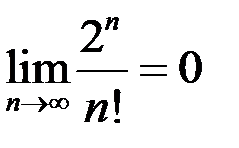 3
3 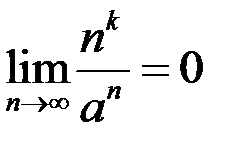 (
( 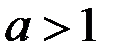 )
)
4. 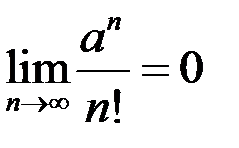 5.
5. 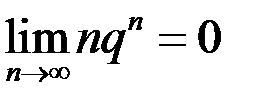 ,
, 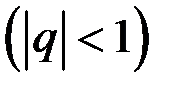 6.
6. 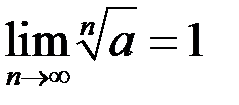 (
( 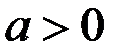 )
)
7. 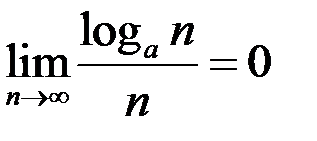 (
( 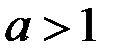 ) 8.
) 8. 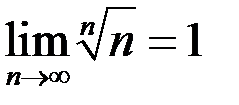 9.
9. 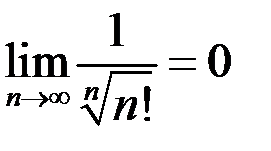 .
.
 И снова тема беспредела
И снова тема беспредела 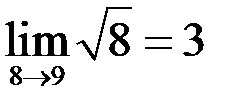 .
.
Предел функции
Определение. Интервал вида 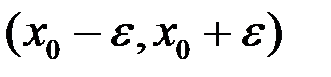 или
или 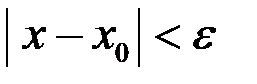 называется
называется 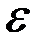 – окрестностью точки
– окрестностью точки 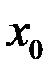 и обозначается
и обозначается 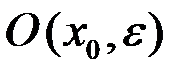 ,
, 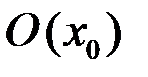 или
или 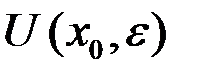 .
.
Проколотой окрестностью точки 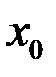 называется окрестность точки
называется окрестность точки 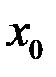 , из которой выброшена (выколота) сама точка. Обозначается
, из которой выброшена (выколота) сама точка. Обозначается 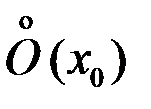 .
.
Окрестностью точки « 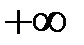 » называется любой бесконечный промежуток (луч) вида
» называется любой бесконечный промежуток (луч) вида 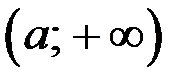 .
.
Окрестностью точки « 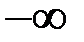 » называется любой бесконечный промежуток (луч) вида
» называется любой бесконечный промежуток (луч) вида 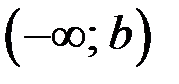 .
.
Окрестностью точки « 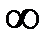 » называется объединение двух окрестностей
» называется объединение двух окрестностей 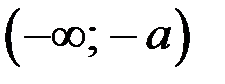 и
и 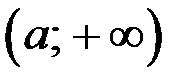 .
.
Определение. Точка 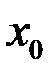 называется внутренней точкой множества
называется внутренней точкой множества 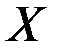 , если эта точка принадлежит данному множеству вместе с некоторой своей окрестностью.
, если эта точка принадлежит данному множеству вместе с некоторой своей окрестностью.
 Определение. Точка
Определение. Точка 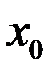 называется предельной точкой множества
называется предельной точкой множества 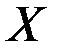 , если в любой окрестности точки
, если в любой окрестности точки 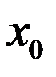 найдется точка
найдется точка 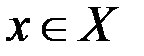 такая, что
такая, что 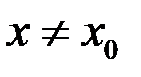 .
.
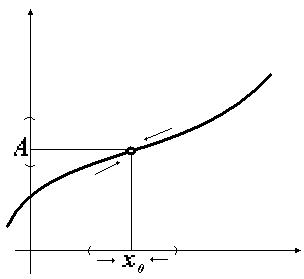
Определение предела объясним на графике (рис. 2).
При приближении к 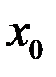 значения функции стремятся к
значения функции стремятся к 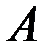 .
.
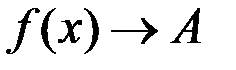 при
при 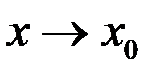 .
.
Определение можно дать как на языке Рис. 2 – Понятие предела последовательности, так и на языке окрестностей.
Пусть точка 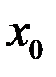 является предельной точкой
является предельной точкой 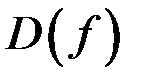 . Пусть функция
. Пусть функция 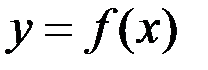 определена в некоторой окрестности точки
определена в некоторой окрестности точки 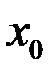 , кроме, может быть, самой этой точки, то есть в
, кроме, может быть, самой этой точки, то есть в 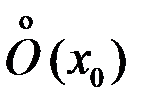 .
.
Определение (по Гейне). Число 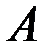 называется пределом функции
называется пределом функции 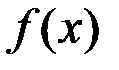 при
при 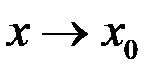 , если
, если 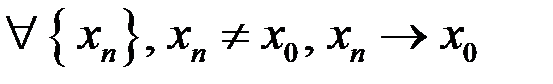 выполнено
выполнено 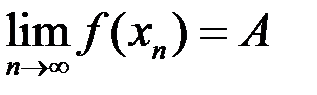 .
.
Определение (по Коши). Число 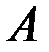 называется пределом функции
называется пределом функции 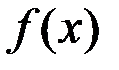 при
при 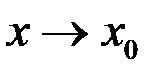 , если для любого сколь угодно малого, заранее заданного
, если для любого сколь угодно малого, заранее заданного 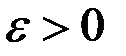 существует такое
существует такое 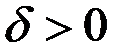 , что для всех
, что для всех 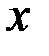 таких, что
таких, что 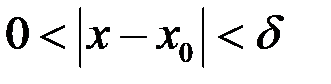 выполняется неравенство
выполняется неравенство 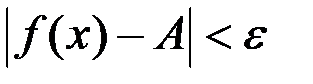 . Или символами
. Или символами
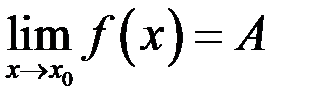
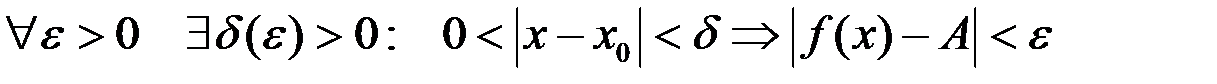 .
.
Теорема (о равносильности двух определений предела). Если функция 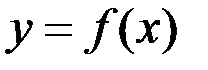 имеет предел в точке
имеет предел в точке 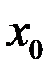 по определению Коши, то она имеет предел и по определению Гейне и наоборот.
по определению Коши, то она имеет предел и по определению Гейне и наоборот.
Пределы, которые мы рассматривали с помощью двухсторонней окрестности, называются двусторонними.
Возможны, однако, односторонние пределы.
При этом 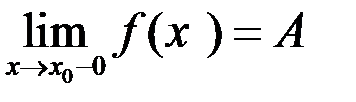 – левый предел;
– левый предел; 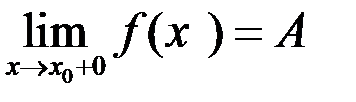 – правый предел.
– правый предел.
В первом случае 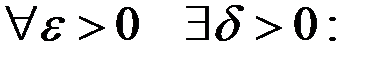
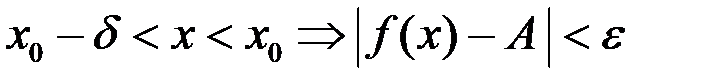 ;
;
Во втором 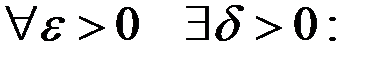
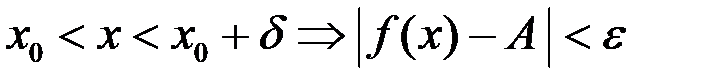 .
.
Задача для самостоятельного решения
1. Для того, чтобы 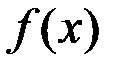 имела в точке
имела в точке 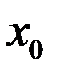 двусторонний предел, необходимо и достаточно, чтобы она имела в этой точке правый и левый пределы и они были равны.
двусторонний предел, необходимо и достаточно, чтобы она имела в этой точке правый и левый пределы и они были равны.
Бесконечно малые функции
Определение. Функция 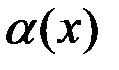 называется бесконечно малой функцией (б.м.), или просто бесконечно малой при
называется бесконечно малой функцией (б.м.), или просто бесконечно малой при 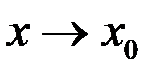 , если
, если 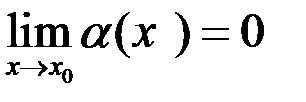 .
.
Б.м. функции имеют важную роль (как и б.м. последовательности). Это связано с тем, что общее понятие предела функции может быть сведено к понятию б.м. функции.
Свойство 1. Предел функции 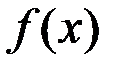 в точке
в точке 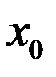 существует и равен числу
существует и равен числу 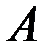 тогда и только тогда, когда функция
тогда и только тогда, когда функция 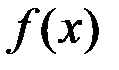 может быть представлена в виде
может быть представлена в виде 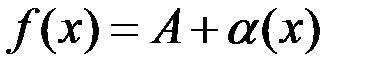 , где
, где 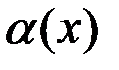 – б.м. при
– б.м. при 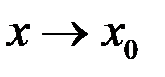 .
.
Свойство 2. Сумма двух б.м. функций при 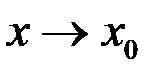 есть б.м. функция.
есть б.м. функция.
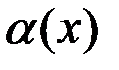 ,
, 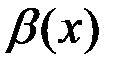 – б.м.
– б.м. 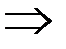
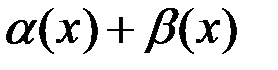 – б.м.
– б.м.
Свойство 3. Произведение двух б.м. функций при 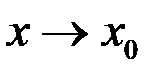 есть б.м. функция.
есть б.м. функция.
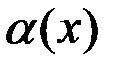 ,
, 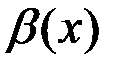 – б.м.
– б.м. 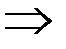
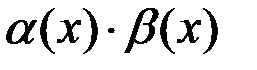 – б.м.
– б.м.
Замечание. Свойства 2 и 3 справедливы для любого конечного числа слагаемых (множителей).
Свойство 4. Произведение б.м. функции на ограниченную при 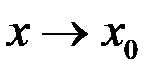 есть функция б.м.
есть функция б.м.
Определение. Функция 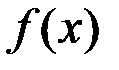 называется бесконечно большой (б.б.) при
называется бесконечно большой (б.б.) при 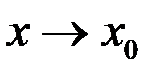 , если
, если 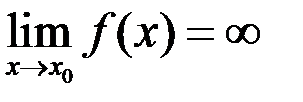 , то есть если
, то есть если
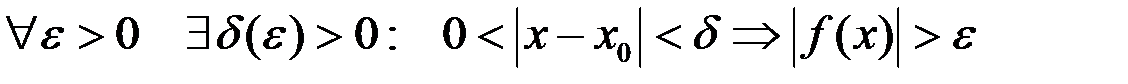 .
.
Свойство 5. Функция 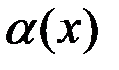 (
( 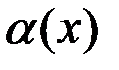
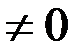 ,
, 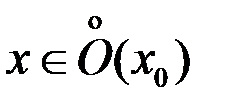 ) есть б.м. функция при
) есть б.м. функция при 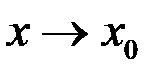 тогда и только тогда, когда
тогда и только тогда, когда 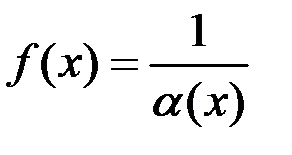 есть б.б. функция.
есть б.б. функция.
По аналогии с конечными односторонними пределами, введем определение и односторонних бесконечных пределов.
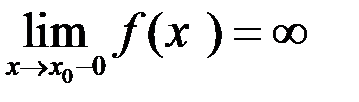
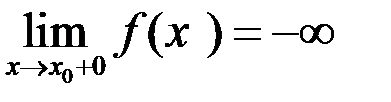 .
.
Бесконечности положительная и отрицательная – это не числа, их можно добавить к множеству действительных чисел 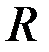 как новые элементы
как новые элементы 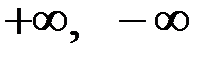 . После этого числовая прямая превращается в так называемую расширенную прямую.
. После этого числовая прямая превращается в так называемую расширенную прямую.
Дата: 2018-11-18, просмотров: 815.