Свойство 1. Б.м. последовательность ограничена.

Свойство 2. Сумма двух б.м. последовательностей есть б.м., разность двух б.м. есть б.м.

Следствие. Сумма и разность любого конечного числа б.м. последовательностей есть б.м.

Задачи для самостоятельного решения

1. Привести пример, когда сумма бесконечного числа б.м. не является б.м.

Свойство 3. Произведение б.м. последовательность на ограниченную есть б.м.

Следствие. Произведение конечного числа б.м. последовательностей есть б.м.

Замечание. Произведение бесконечного числа б.м. последовательностей не обязательно б.м.

Пример. 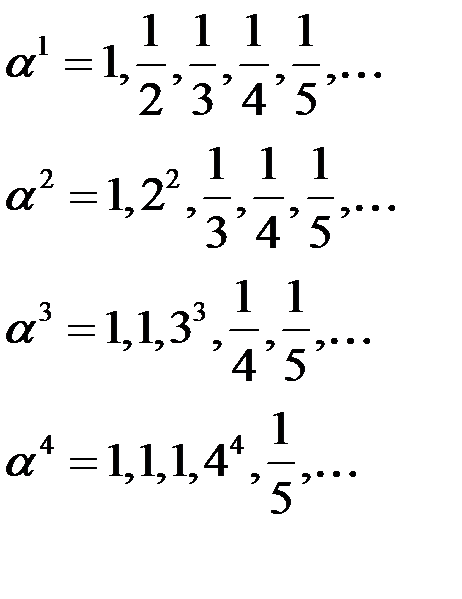 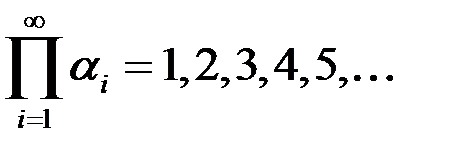             – б.б.

Задачи для самостоятельного решения

1. Известно, что 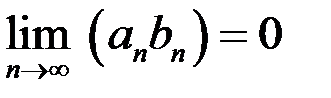. Следует ли отсюда, что

А) 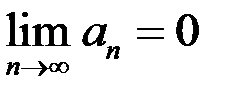 и .

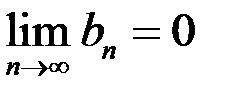Б) Хотя бы одна из последовательностей 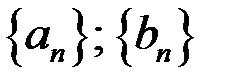 – б.м.

2. Пусть 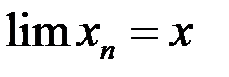, где .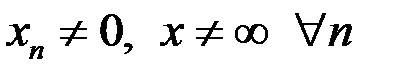

А) Существует ли ?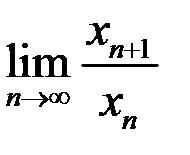

Б) Доказать, что если этот предел существует и равен 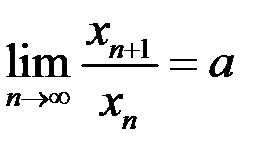, то .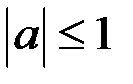

В) Может ли последовательность 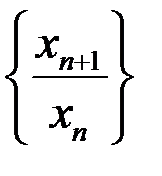 быть неограниченной?

Свойство 4. Если последовательность 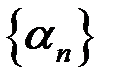 (  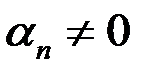) б.м., то  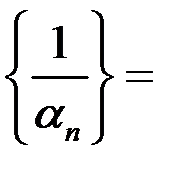б.б.

Свойство 5. Для того, чтобы число 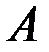 было пределом последовательности 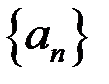, необходимо и достаточно, чтобы разность  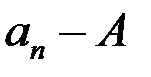была б.м.

Следствие. Последовательность 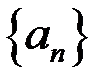 имеет конечный предел  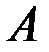тогда и только тогда, когда ее можно записать в ви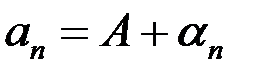де , где 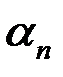 – б.м.

Свойства сходящихся последовательностей

Свойство 1. Если последовательность имеет конечный предел, то она ограничена.

Если мысли сходятся, то они ограничены.

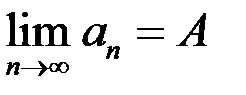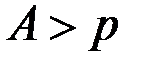Свойство 2. А) Если  и , то ;

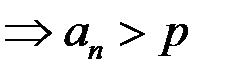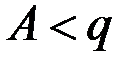Б) Если  и , то .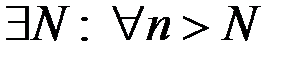

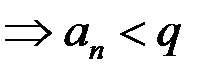Свойство 3. Сходящаяся числовая последовательность не может иметь более одного предела.

Свойства, связанные с арифметическими операциями над последовательностями

Свойство 4. Если .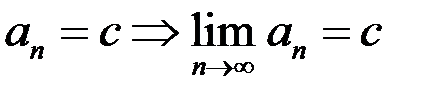

Свойство 5. Если существуют конечные 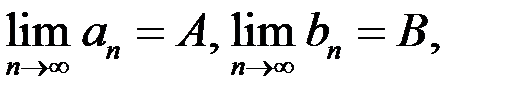то существует .

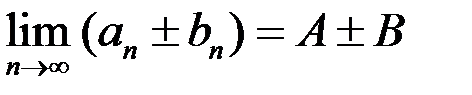Свойство 6. Если существуют конечные то существует .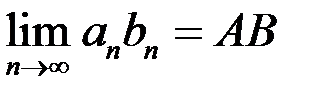

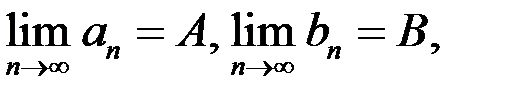
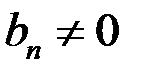
Свойство 7. Если существуют конечные 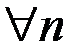, , 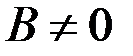то существует .

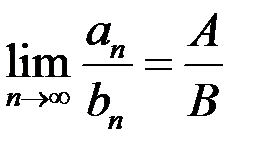Замечание. Свойства 5, 6 справедливы для любого конечного числа слагаемых и сомножителей.

Свойства, связанные с неравенствами для последовательностей

Свойство 8. Если существуют 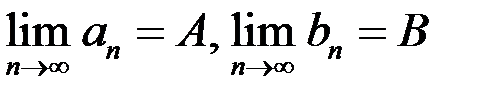 и , тогда : .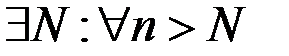

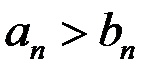Свойство 9. (теорема о предельном переходе в неравенствах).

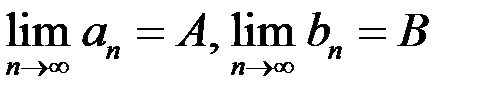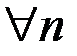
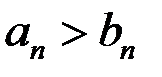Если существуют  и , то .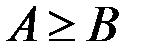

Замечание. Хотя 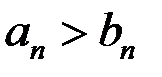(строго), но 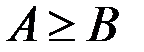(не строго).

Пример. .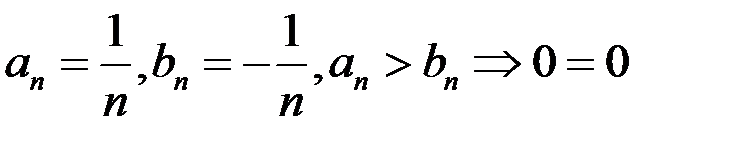

Определение. Говорят, что последовательность отделена от нуля, если 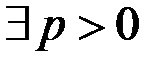 такое, что .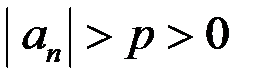

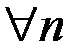Свойство 10. Если 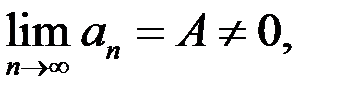 то , .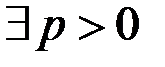

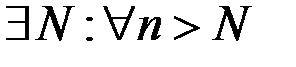
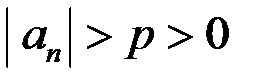(здесь, если , то 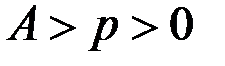, а в случае ).

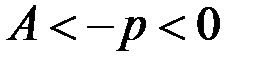Свойство 11. Если 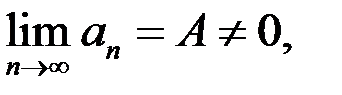то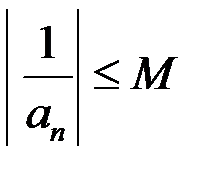

(это следствие свойства 10).

Свойство 12. (теорема о сходимости промежуточной последовательности, или о двух милиционерах).

Есл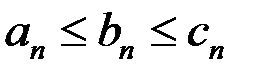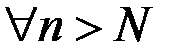и  и 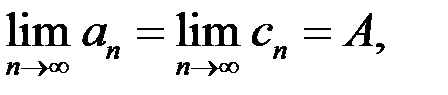 то последовательность  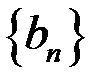сходится и .

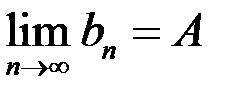Задача для самостоятельного решения

1. Доказать, что отбрасывание или присоединение конечного числа элементов последовательности не влияет на ее сходимость.