Пусть твердое тело вращается относительно оси под действием нескольких сил суммарный момент относительно той же оси, тогда А приводит к изменению Ек этого тела
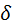А= 
А=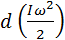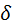Mdφ=Mωdt d 
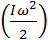= Mωdt
dφ=ωdt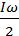 
*2dω= Mωdt
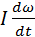=M
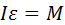всегда М↑↑ε
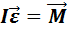- основное уравнение динамики вращательного движения
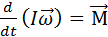- выражает основной закон динамика вращ. движения
Момент импульса тела относительно точки – физическая величина равная векторному произведению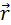 
проведенного из центра в точку на импульс этой точки.
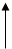
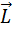
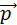
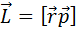
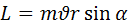
O 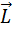перпендикулярна плоскости в которой
лежат вектора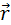 
и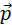 
при определенных условиях момент импульса L=const
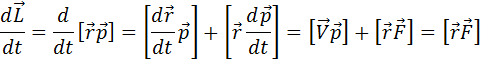
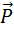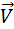
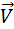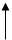=m 
↑↑ 
M=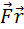 
- момент силы
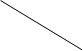
M=rFsinα=Fl
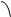
l=rsinα – перпендикуляр опущенный
из данного центра на линию действия
силы – плечо силы относительно центра
Если М действующее на тело окажется = 0 то L будет сохраняться такое явление при котором будет наблюдаться движение тела под действием центральных сил.
= 
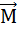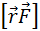
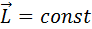
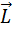перпенд.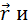 
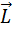перпенд. 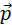то 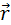перпен. одной и той же прямой значит что точка должна двигаться в плоскости перпенд. L и проходящей через центр силы.
В зависимости от начальных условий и от характера действия начальной силы точка будет двигаться по окружности эллипсу и параболе.
Для системы мат. точек скорость изменения момента импульса суммы равна полному моменту всех внешних сил действующих на тело системы.
Если система замкнута то полный момент внешних сил =0 и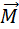 
остается постоянным, вывод справедлив для любого числа мат. точек.
Вопрос 17. Элементы специальной теории относительности. Принцип относительности в классической механике. Преобразования Галилея. Постулаты специальной теории относительности. Преобразования Лоренца.
Пусть задана неподвижная система отсчета k(x,y,z) и k’ движущаяся относительно k со скоростью v0. В начальный момент времени начальные координаты совпадают.
Найдем формулы преобразования
координат при переходе от одной
системы отсчета к другой
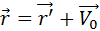t (1.1)
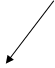
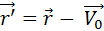t
Кроме того t’=t (1.2) время в
классической физике протекает во
всех системах отсчета одинаково.
Длина отрезков и время не зависит от состояния движения и одинаковы во всех системах отсчета; предложение об абсолютности пространства и времени лежит в самой основе представления ньютоновской механики – представления основываются на экспериментальном материале относящиеся к изучению движения со скоростями, значение меньше скорости света в вакууме.
Соотношения 1.1 и 1.2 представляют преобразования Галилея
x’=x – V0t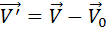 
(1.4)
y’=y (1.3) V0=const
z’=z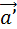 
= 
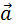
t’=t
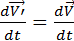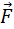m 
= 
m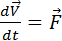 
Второй закон ньютона записывается в ИСО k’ также как и в ИСО k одинаковыми оказываются и все следствия. Законы механики одинаковы во всех ИСО – принцип относительности Галилея (з. механики инвариантны).
Постулаты. Ньютоновская механика справедлива для тел движущимися со скоростями << скорости света в вакууме (с=3*108 м/с). Для описания движения совершаемой со V сравнимыми со с Эйнштейн создал релятивистскую механику т.е. механику учитывающую требования СТО. Созданная Эйнштейном в 1905 СТО представляет собой физическую теорию пространства и времени для случая пренебрежимо малых гравитационных полей. Термин «специальная» подчеркивает то обстоятельство что эта теория рассматривает явления только в ИСО. СТО основывается на двух постулатах:
Принцип относительности Эйнштейна. Все физические явления протекают одинаковым образом во всех ИСО, все законы природы и уравнения их описывающие инвариантны (не меняются) при переходе от одной ИСО к другой, другими словами в ИСО эквивалентны (не различимы) по физ. свойствам. Никакими опытами нельзя выбрать ни одну из них как предпочтительную.
Принцип постоянства скорости света. с одинакова во всех ИСО и не зависит от движения источников и приемников света
из постулатов Эйнштейна следует что с является предельной: никакой сигнал никакое воздействие не могут распространяться со V>c. Именно предельный характер объясняет одинаковую с во всех системах отсчета. Все содержание СТО вытекает из этих 2х ее постулатов. В настоящее время оба постулата как и все следствия из них убедительно подтверждаются всей совокупностью эксперементного материала.
Преобразования Лоренца. Преобразования Галилея противоречат 2-ому постулату СТО → были выдвинуты новые преобразования.
Рассмотрим k и k’, t=t’. Пусть в начальный момент времени начальные координаты совпадают, в этот момент времени из т. О излучается световой импульс. Рассмотрим полноту фронта этого импульса в t и t’
x-x’=c(t-t’)
т.к x≠x’ → t≠t’ (3.1)
время в системах отсчета k и k’ течет по разному
в согласии с постулатами Эйнштейна находятся преобразования Лоренца.
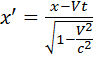V – скорость системы k’ относительно k
y=y’ (3.2) V<<c то преобразования Лоренца переходят в
z=z’ преобразования Галилея
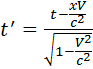преобразования Лоренца теряют смысл если V>c
Дата: 2018-11-18, просмотров: 908.
