Для характеристики внешнего механического воздействия на тело, приводящего к изменению его вращательного движения, вводится понятие момента силы. Различают момент силы относительно неподвижной точки (полюса) и относительно неподвижной оси.Моментом силы относительно полюса называется векторная величина, равная векторному произведению радиус - вектора, проведённому из полюса в точку приложения силы, на вектор силы,т.е. 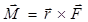 . В скалярной форме
. В скалярной форме 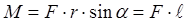 , где
, где 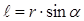 - плечо силы относительно рассматриваемого полюса, т.е. длина перпендикуляра, проведённого из полюса на линию действия силы, a - угол между вектором силы и радиус-вектором. Момент силы – псевдовекторная величина. Если линия действия силы проходит через полюс, то её момент силы равен нулю.
- плечо силы относительно рассматриваемого полюса, т.е. длина перпендикуляра, проведённого из полюса на линию действия силы, a - угол между вектором силы и радиус-вектором. Момент силы – псевдовекторная величина. Если линия действия силы проходит через полюс, то её момент силы равен нулю.
Момент постоянной силы, при неизменном положении точки её приложения, относительно одного и того же полюса, также постоянен. Момент силы равен нулю, если линия действия силы проходит через полюс.Главным моментом (результирующим моментом) системы сил относительно полюса называется векторная величина, равная векторной сумме моментов относительно этого полюса всех сил системы, т.е. 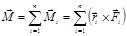 ,где
,где 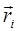 - радиус-вектор, проведённый из полюса в точку приложения силы
- радиус-вектор, проведённый из полюса в точку приложения силы 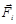 .
. 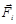 - внешняя сила, внутренние силы не создают моментов, т.к. их моменты взаимно компенсируют друг друга.Из третьего закона Ньютона следует, что
- внешняя сила, внутренние силы не создают моментов, т.к. их моменты взаимно компенсируют друг друга.Из третьего закона Ньютона следует, что 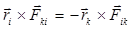 , где
, где 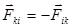 внутренние силы, характеризующие взаимодействие между «i -ой» и «k -ой» точками системы, следовательно, создаваемые внутренними силами моменты взаимно компенсируют друг друга и при вычислении главного момента не учитываются.Моментом силы относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента силы относительно произвольной точки данной оси.В частном случае вращательного движения точки по окружности, момент силы, лежащей в плоскости вращения, равен
внутренние силы, характеризующие взаимодействие между «i -ой» и «k -ой» точками системы, следовательно, создаваемые внутренними силами моменты взаимно компенсируют друг друга и при вычислении главного момента не учитываются.Моментом силы относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента силы относительно произвольной точки данной оси.В частном случае вращательного движения точки по окружности, момент силы, лежащей в плоскости вращения, равен 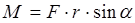 , где a - угол между радиусом окружности и силой .Если же сила находится под углом к плоскости вращения, то её момент относительно неподвижной оси равен
, где a - угол между радиусом окружности и силой .Если же сила находится под углом к плоскости вращения, то её момент относительно неподвижной оси равен 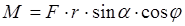 , где
, где 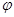 - угол наклона силы к плоскости вращения. Если вращение происходит по окружности и сила является касательной, то её момент относительно неподвижной оси равен
- угол наклона силы к плоскости вращения. Если вращение происходит по окружности и сила является касательной, то её момент относительно неподвижной оси равен 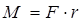 . Главный момент (результирующий момент) относительно неподвижной оси системы сил равен алгебраической сумме моментов относительно этой оси всех сил системы, т.е.
. Главный момент (результирующий момент) относительно неподвижной оси системы сил равен алгебраической сумме моментов относительно этой оси всех сил системы, т.е. 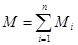 .
.
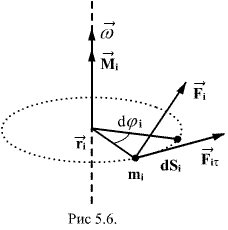 Рассмотрим действие внешней силы
Рассмотрим действие внешней силы  , приложенной к точке массой
, приложенной к точке массой 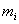 . За время
. За время 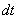 элементарная масса
элементарная масса 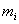 проходит путь
проходит путь 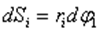 Работа силы
Работа силы 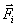 на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей
на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей 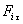 силы.
силы.
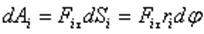
Но 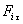 равна модулю момента
равна модулю момента 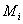 силы
силы 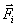 относительно оси вращения. Работа
относительно оси вращения. Работа 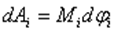 , и будет положительна, если
, и будет положительна, если 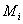 имеет такое же направление, как и
имеет такое же направление, как и 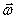 отрицательное, если направление векторов
отрицательное, если направление векторов 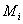 и
и 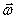 противоположны.
противоположны.
С учетом, что 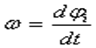
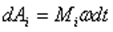
Работа всех сил, приложенных к телу 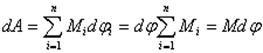
Полная работа 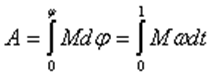
Дата: 2018-11-18, просмотров: 997.