Движение абсолютно твердого тела-движение такого тела, взаим распол частиц которого вовремя его движения не меняется. Простым видом движ тв тела явл поступательное движение(все точки тела движутся одинаково)

Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.

Вращательное движение твердого тела вокруг неподвижной оси-это движение, при котором все точки тела движутся по окружностям , центры которых лежат на одной прямой, называемой осью вращения. Угловая скорость – векторная величина, характеризующая быстроту вращения тела; отношение угла поворота ко времени, за которое этот поворот произошёл; вектор, определяемый первой производной угла поворота тела по времени. Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта. ω(скорость поворота радиус-вектора рад/с)=dφ/dt=2π/T=2πn, где T – период вращения, n – частота вращения. ω=lim_Δt→0Δφ/Δt=dφ/dt.условились считать, что вектор омега направл в ту сторону перпендик плоскости движения материальной точки глядя из которой мы видим движение материальн точки против часовой стрелки.

Угловое ускорение – вектор, определяемый первой производной угловой скорости по времени;вектор, характ быстроту изменения угловой скорости.При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. Вторая производная угла поворота по времени. При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору φ, при замедленном – противонаправлен ему. ε=dω/dt.

ε сонапр с ω dω/dt>0, и наоборот если dω/dt<0.

4. Принцип инерции (Первый закон Ньютона). Инерциальные системы отсчёта. Принцип относительности.

Первый закон Ньютона (закон инерции): всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние

Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют законом инерции.

Первый закон Ньютона утверждает существование инерциальных систем отсчёта.

Инерциальная система отсчёта – это система отсчёта, относительно которой свободная материальная точка неподверженная воздействию других тел, движется равномерно прямолинейно; это такая система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы.

Принцип относительности - фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе в состоянии равномерного прямолинейного движения. Состояния движения или покоя определяются по отношению к произвольно выбранной инерциальной системе отсчета. Принцип относительности лежит в основе специальной теории относительности Эйнштейна.

Принцип относительности (Галилея): никакие опыты (механические, электрические, оптические), проведённые внутри данной инерциальной системы отсчёта, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчёта к другой.

5. Преобразования Галилея.

Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой.

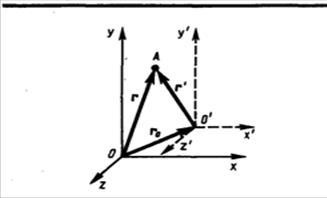
Рассмотрим две системы отсчета: инерциальную систему К (с координатами x,y,z), которую условно будем считать неподвижной и систему К’ (с координатами x’,y’,z’), движущуюся относительно К равномерно и прямолинейно со скоростью U (U = const). Найдем связь между координатами произвольной точки А в обеих системах. r = r’+r₀=r’+Ut. (5.1.)

Уравнение (5.1.) можно записать в проекциях на оси координат:

x=x’+U_xt;

y=y’+U_yt; (5.2.)

z=z’+U_zt;

Уравнение (5.1.) и (5.2.) носят название преобразований координат Галилея.В частном случае, когда система К' движется со скоростью т вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат Галилея имеют вид

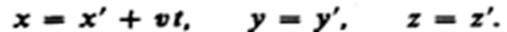
В классической механике предполагается, что ход времени не зависит от относи­тельного движения систем отсчета, т. е. к преобразованиям (34.2) можно добавить еще одно уравнение:

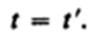
Записанные соотношения справедливы лишь в случае

классической механики (u<<с)