Обратимым называется такой термодинамический процесс который может протекать как в прямом так и в обратном направлении. Система проходит через те же самые промежутки что и в прямом направлении но в обратном порядке, причем без того чтобы в окружающей среде оставались изменения. Всякий процесс неудовлетворяющий этим условиям называется необратимым. Мерой необратимости процесса в замкнутой системе является изменением новой функции состояния - энтропии, существование которой у равновесной системы устанавливает первое положение второго начала о невозможности вечного двигателя второго рода . Однозначность этой функции состояния приводит к тому, что всякий необратимый процесс является неравновесным. если бы энтропия была неоднозначной функцией состояния то , можно было бы осуществить вечный двигатель второго рода. Положение о существовании у всякой термодинамической системы новой однозначной функцией состояния энтропии S, которая при адиабатных равновесных процессах не изменяется и составляет содержание второго начала термодинамики для равновесных процессов. Математически второе начало термодинамики для равновесных процессов записывается уравнением: dQ/T = dS или dQ = TdS. Интегральным уравнением второго начала для равновесных круговых процессов является равенство Клаузиуса : dQ/T = 0. Для неравновесного кругового процесса неравенство Клаузиуса имеет следующий вид : dQ/T < 0. Теперь можно записать основное уравнение термодинамики для простейшей системы находящейся под всесторонним давлением :

TdS = dU + pdV . Второе начало термодинамики является обобщением опытных фактов. Оно установило максимально возможные пределы, превращения внутренней энергии в механике, в круговые процессы, утверждая невозможное получение работы за счет тел находящихся в тепловом равновесии, указывая направление протекания самопроизвольных процессов. Постулат Клазиуса: 1) Невозможен термодинамический процесс каким бы способом мы не пытались его осуществить единственным конечным результатом которого была бы передача внутренней энергии от менее нагретого тела к более. Под словами «единственным результатом которого» следует понимать, что процесс происходит самопроизвольно не вызывая изменения в окружающей среде. 2)Невозможна некомпенсированная передача внутренней энергии от менее нагретого тела к более нагретому. Постулат Томсона: 1)Невозможен круговой процесс каким бы способом мы не пытались его осуществить единственным конечным результатом которого было бы превращение внутренней энергии взаимствованной из какого либо тела путем теплообмена в механическую энергию путем совершения работы. Невозможен некомпенсированный переход тепла в работу. Невозможно построить вечный двигатель второго рода – это тепловая машина КПД=1. Формулировки Клазиуса и Томсона можно показать эквивалентными.

Вопрос 36.Энтропия. Энтропия и законы термодинамики. примеры вычисления энтропии.

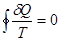- обратимый цикл; 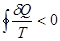- необратимый цикл }=> интегралы Клазиуса и являются математической записью 2 Н т/д. Интегралы Клазиуса не зависят от того каким путем мы переводим систему из одного состояния в другое а выражение δQ/T – является полным дифференциалом некоторой функции S являющийся функцией состояния. Эту функция назвали энтропией. Энтропия, функция состояния S термодинамической системы, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты 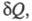полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре Т: dS=δQ/T. 1/T – интегральный множитель для δQ. [S]= Дж/К. Поскольку dS= δQ/T, a δQ – алгебраическая величина, то изменения энтропии dS зависит от того какой знак имеет δQ. δQ>0, dS>0 – энтропия возврастает, δQ<0 ,dS<0-убывает, δQ=0 – адиабатный процесс, то dS =0 – энтропия не изменяется. Энтропия обладает свойством аддитивности: энтропия всей системы состоит из нескольких частей равных сумме энтропийных частей этой системы. Если система изолирована и не получает тепло извне δQ=0, то S2-S1>0 - энтропия изолированной системы в которой протекают необратимые процессы возрастает. Изолированной назыв система окруженная жесткой адиабатной оболочкой (жесткой – не позволяет совершать работу над системой, адиабатной – препятствует охлаждению). Если в изолированной системе протекает только обратимые процессы то 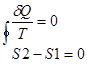, S=const – энтропия изолированной системы в которой протекает обратный процесс остается неизменный. Энтропия изолированной системы при любых процессах протекающих в ней не убывает. Поскольку все реальные процессы являются необратимыми то в изолированной системе они сопровождаются ростом энтропии. Энергия изолированной системы (И.С.) постоянная, то энтропия не может служить показателем того в каком направлении протекает процесс в этой системе. В конечном состоянии в И.С. энтропия всегда не меньше чем начальном. По изменению энтропии мы можем сказать в каком направлении протекает процесс. Энтропия возрастает до определенного значения. Закон возрастания энтропии в И.С.: энтропия И.С. стремится к максимуму. Примеры вычисления энтропии: 1 Н Т/Д:  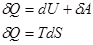|=> |=> 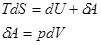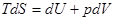- обобщенная математическая запись 1 Н Т/Д и 2 Н Т/Д – основное уравнение термодинамики.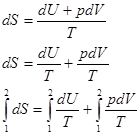  

1. Изменение энтропии идеального газа при переходе из 1-2: 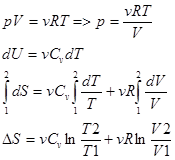- изменение энтропии v-молекул идеального газа при переходе из 1-2.

1) V=const. 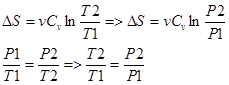      2) T=const.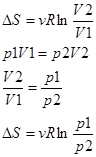

3) p=const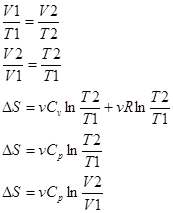

2. Изменение энтропии при плавлении. При p= const – плавление происходит при T=const.

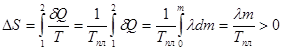. Приведенные примеры вычисления энтропии показывают что по изменению энтропии можно судить о направлении протекающих процессов.