Рассмотрим поведение молекул атм. воздуха в поле тяготения земли, благодаря силам тяготения и тепловому движению молекул в земной атмосфере установилось определенное распределение молекул по высоте, а следовательно возникает распределение n молекул и p воздуха в зависимости от высоты. Выведем барометрическую формулу которая выражает закон изменения атмосферного давления с высотой. Построим физическую модель для этого делаем допущения: 1)атмосферу воздуха рассматриваем как идеальный газ находящийся в состоянии термодинамического равновесия при чем температура этого газа с высотой не меняется; 2)g будем считать постоянным и с высотой не меняющимся.

Рассмотрим б.м. приращение столба воздуха на котором можно плотность воздуха считать постоянным.

 Этому приращению высоты соответствует приращение давления: 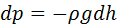 ; знак “-“ показывает что если dh>0 то dp<0 и наоборот

т.к идеальный газ находится в состоянии термодинамического равновесия то воспользуемся УМК:

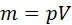
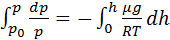
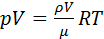                               lnp|^p_p0=-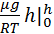

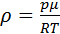
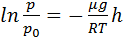                                     ; e=e

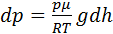
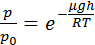
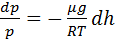
                          (6.1) – бараметрическая формула

                                                                          Закон распределения p с высотой

На основе этой формулы действуют приборы служащие для измерения высоты- альтиметры, представляют барометры шкалы которых градуируются в метрах при этом вносятся поправки учитывающие понижение температуры с высотой.

Выберем систему так что на высоте h=0 p₀=n₀kT, тогда на высоте h, p=nkT

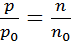
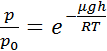
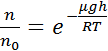
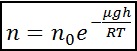 (6.2)

Если g=0 (в отсутствие гравитационного поля) n=n₀, т.е если бы не было земного тяготения то тепловое движение молекул привело бы к установлению во всем мировом пространстве одинаковой концентрации молекул. Если бы не было теплового движения но присутствовало гравитационное поле то молекулы всей атмосферы сосредоточились бы тонким слоем у поверхности земли. На самом деле осуществляется компромисс и возникает определенное распределение n молекул по высоте.

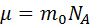
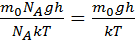
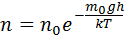  (6.3)

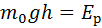
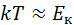
Распределение n молекул воздуха по высоте зависит от соотношения 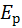 и теплового хаотического движения.

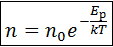 (6.4) – молекулы распределяются с большей плотностью там где  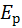меньше

Больцман доказал что распределение молекул по высоте является универсальным и остается справедливым для любых частиц совершающих тепловое движение в любом потенциальном поле. Соотношение 6.4 выражает распределение Больцмана.

Распределение Максвелла задает распределение молекул по скоростям, закон Больцмана задает распределение по 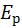 а т.к 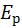 зависит от координат то этот закон дает распределение по координатам.