Рассмотрим идеальный газ в состоянии термодинамического равновесия. Из-за того что число значений скоростей бесконечна а число молекул несмотря на то что велико все же конечно, то неправильно ставить вопрос о том сколько молекул в данном объеме V газа движется со скоростью .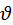

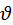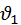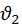В объеме даже при большом числе молекул может не оказаться ни одной молекулы которая удовлетворяет данному требованию, поэтому можно вести речь лишь о том сколько молекул движется со скоростью  значение которых лежат в интервале от  до  (и то с определенной вероятностью).

Поведение газа состоящего из огромного числа молекул подчиняется законам статистики и теории вероятности закон распределения молекул по скорости был получен Максвеллом в к. 19 века.

Пусть d_n – число содержащихся в единице объема молекул в интервале от 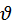 до 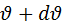. dn зависит от общего числа частиц n в V и ширины интервала скоростей.

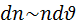
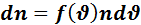 (4.1)

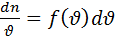 - величина показывает какая часть общего числа молекул обладает  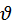лежащими в интервале шириной d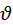

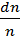 – вероятность того что из n молекул dn молекул обладают скоростями лежащими в интервале шириной d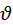

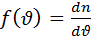 – плотность вероятности

Пользуясь методами теории вероятности Максвелл теоретически вид этой функции представляющей собой аналитическое выражение статистического закона распределения абсолютных величин скоростей молекул

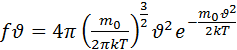 (4.2) - функция распределения.  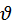- любое число от 0 до  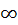абсолютное значение скорости молекулы.

Если учесть 4.1 и 4.2 то можно получить выражение для числа частиц 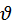 лежат в заданном интервале скоростей

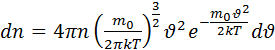 (4.3)

Физ смысл функции распределения: площадь заштрихованной фигуры численно равна доле молекул 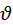 которых попадают в интервал от  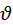до 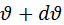. При этом S под всей кривой всегда равна 1.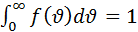

Позднее Больцман показал что каким бы ни было распределение молекул по скоростям при постоянной Т оно становится Максвелловским. Максимуму кривой распределения соответствует наивероятнейшая скорость

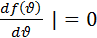
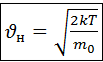                             (4.4)

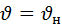
Не верно говорить что наибольшая вероятность 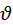 - это 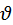 которой обладает наибольшее число молекул.

Наивероятнейшая 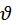- это 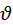 в окрестности которой на данный интервал скоростей приходится большее число молекул чем в окрестности любой другой скорости.

Соотношение 4.3 можно переписать в виде: 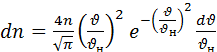 (4.5)

Функция распределения молекул по скоростям позволяет вычислить среднее арифметическое скорости молекул: 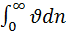 – просуммируем по всем значениям  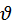молекул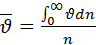

После подстановки 4.5 и интегрирования можно получить:

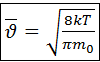 (4.6)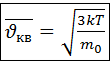  

Эти скорости являются тремя важнейшими характеристиками состояния газа

Зависят от массы молекул и температуры и отличаются только численным множителем: 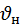: : 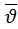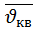=1:1,13:1,22                <

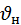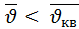
т.к правая часть кривой функции распределения более пологая то следует что в газе преобладают молекулы движущиеся со скоростями большими чем наивероятнейшая скорость.

На распределение молекул по скоростям большое внимание оказывает температура с увеличением Т максимум функции распределения будет уменьшаться а наибольшее 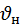 соответствующее ему будет увеличиваться

S криволинейных трапеций одинаковы с повышением Т доля быстрых молекул возрастает и это сильно влияет на физ.-хим. процессы.

Закон Максвелла справедлив в отсутствие внешних силовых полей.

1-ое экспериментальное определение 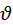 молекул было проведено Штерном в 1920г.

Пучок атомов серебра проходит через щель и осаждается на внутренней поверхности большего цилиндра напротив щели если цилиндр неподвижен. Если привести прибор во вращательное движение то след который оставляет пучок атомов серебра на внутренней поверхности большего цилиндра будет смещаться потому что за 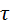  пока атомы серебра пройдут расстояние от внутреннего цилиндра к наружному прибор успеет повернуться на некоторый угол и в результате против пучка оказывается другой участок наружного цилиндра который смещается на  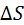от первоначального положения.

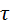 - время прохождение атомов серебра между цилиндрами.

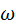 - угловая скорость вращения

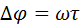
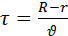
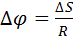
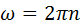                     n-частота вращения

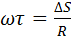
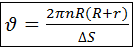
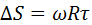
Опыты показали что в случае покоищахся цилиндров границы полоски были четкими а в случае движения цилиндров размытыми. Это свидетельствует о том что атомы серебра движутся с различными скоростями более быстрые атомы быстрее достигают внутренней поверхности цилиндра и смещаются на меньший угол чем более медленные.

Исследования методом поглощения света показали что толщина полоски различны и имеет вид

Результат опыта Штерна подтвердил правильность оценки 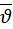 атомов серебра которая вытекла из распределения Максвелла. Недостаток опыта Штерна в том что 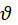атомов измерялась в пучке а распределения Максвелла выводились для беспорядочного движения молекул.