Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси, проходящей через тело. Мысленно разобьём это тело на маленькие объёмы с элементарными массами m₁, m₂,…,m_n, находящиеся на расстоянии r₁, r₂,…, r_n, от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы опишут окружности различных радиусов r_i и имеют различные линейные скорости υ_i. Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов.

T_вр=∑ⁿ_i=1m_iυ_i²/2=∑ⁿ_i=1m_iω²r_i²/2=(ω²∑ⁿ_i=1m_ir_i²)/2=I_zω²/2, 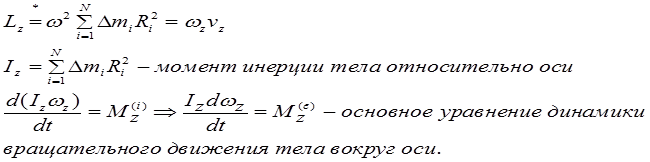где I_z – момент инерции тела. Вращение твёрдого тела вокруг неподвижной оси:

Можно показать, что проекция момента импульса на ось “Z” может быть записана таким образом:

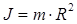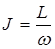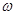где R – расстояние до оси. Моментом инерции материальной точки относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также , где - угловая скорость тела относительно данной оси.Моментом инерции системы материальных точек относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой системы при вращательном движении и, равная алгебраической сумме произведений масс всех материальных точек системы на квадрат их расстояний до оси, т.е. 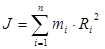.Момент инерции определен только относительно оси.В случае непрерывного распределения масс с плотностью сумма за­менится на интеграл по всему объему тела:  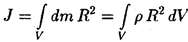 (Интегрирование производится по всему объёму; пределы интегрирования устанавливаются исходя из конфигурации тела и его размеров). Если тело однородно, то его плотность во всех точках постоянна и r можно вынести из-под знака интеграла.Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему, т.е. .

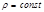1. Момент инерции обруча относительно оси, перпендикулярной к его плоскости и проходящей через его центр. Обруч считается бесконечно тонким, т.е. толщиной обода можно пре­небречь по сравнению с радиусом R .. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R² можно вынести из-под знака интеграла: 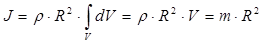, где m — полная масса обруча Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр. Диск считается бесконечно тонким, т.е. его толщина много меньше ра­диуса R. Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусом s и толщиной ds.Момент инерции диска относительно перпендикулярной оси, проходящей через центр(цилиндр).J=mr²/2. Момент инерции шара относительно его диаметра. Поступим аналогичным образом: "нарежем" шар на бесконечно тон­кие диски толщиной dz . находящиеся на расстоянии z от центра J=2/5mR²Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню.J=ml²/12 Физический смысл момента инерции: Инерционные свойства при поступательном движении характеризуются только массой тела, т.е. зависит только от массы. Инерционные свойства при вращательном движении характеризуются моментом инерции, т.е. зависят от его массы, расстояния до оси вращения и расположению теда по отношению к этой оси. Последнее означает, что относительно двух разных осей инерционные свойства вращательного движения одного и того же движения тела будут разными. Теорема Штейнера:Момент инерции тела, относительно произвольной оси равен сумме момента инерции тела относительно оси центра тяжести и произведения массы тела на квадрат расстояния до выбранной оси. момент инерции тела относительно произвольной оси вращения равен сумме момента инерции Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а - расстояние от центра инерции тела до выбранной оси вращения, т.е. 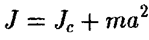, где m - масса тела, а - расстояние от центра инерции тела до выбранной оси вращения.