Потенциальная энергия – энергия частиц во внешнем потенциальном поле.

Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия определяется с точностью до некоторой постоянной. Это не отражается на физических законах, так как в них входят или разность потенциальных энергий в двух положениях тела, или производная потенциальной энергии по координатам. Поэтому потенциальную энергию тела в каком-то определённом положении считают равной нулю (выбирают нулевой уровень отсчёта), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Работа потенциальных сил при малом изменении конфигурации системы - dА = - dW.Данные соотношения справедливы для случая стационарного (не зависящего от времени) внешнего потенциального поля. Для простейшего случая, нахождения материальной точки во внешнем потенциальном поле, сила с которой это поле действует на точку, вычисляется по формуле: ,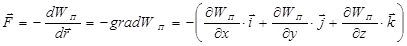

где 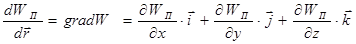  - называется градиентом скалярной функции (в данном случае - потенциальной энергии). Градиент - это векторная величина, направленная в сторону роста значений функции U. В приведённой формуле фигурирует знак «-», который указывает, что сила направлена в сторону убыли значений функции U.

Энергия кинетическая и потенциальная. Полная механическая энергия и закон ее сохранения. Примеры применения законов сохранения энергии.

 Кинетической энергией тела называется энергия его поступательного движения.. Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона: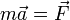

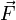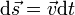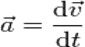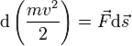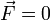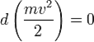— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим: Если система замкнута, то есть , то , а величина 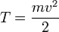остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

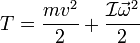
где: 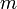— масса тела 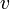— скорость центра масс тела 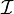— момент инерции тела 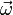— угловая скорость тела.

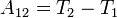
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия определяется с точностью до некоторой постоянной. Это не отражается на физических законах, так как в них входят или разность потенциальных энергий в двух положениях тела, или производная потенциальной энергии по координатам. Поэтому потенциальную энергию тела в каком-то определённом положении считают равной нулю (выбирают нулевой уровень отсчёта), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Работа совершается за счет убыли потенциальной энергии:dA=-dП. Для консервативных сил:

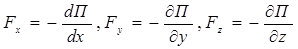.Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела с массой m, поднятого на высоту h поверхностью земли равна П=mgh,Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком: A = –(E_р2 – E_р1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел: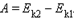

Следовательно 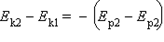или E_k1 + E_p1 = E_k2 + E_p2

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = E_k + E_p называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

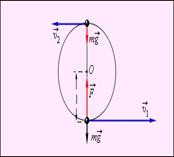Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости Рис поясняет решение этой задачи.

Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде: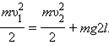

Обратим внимание на то, что сила F натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы. 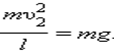, 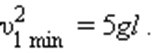. 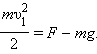Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно

Прочность нити должна, очевидно, превышать это значение.

F = 6mg

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.

12. Центральный удар абсолютно упругих шаров. Расчет скорости шаров после соударения. Соударение двух шаров с резко отличающимися массами. Ударом называется столкновение тел, при котором за весьма короткий промежуток времени происходят значительные изменения скоростей сталкивающихся тел. Удар называется централь­ным, если тела до удара движутся вдоль прямой, проходящей через их центры инерции.Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие виды энер­гии. Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса. Обозначим скорости шаров массами m₁ и m₂ до удара через ν₁ и ν₂, после удара - через ν₁' и ν₂' . Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево. При указанных допущениях законы сохранения имеют вид: 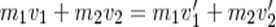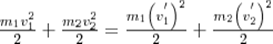Произведя соответствующие преобразования в выражениях,получим 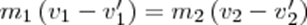(3), 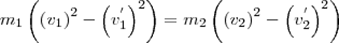откуда 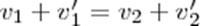(5). Решая уравнения(3)(5)получаем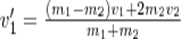 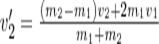.При ν₂=0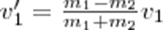  

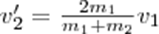
а) m₁=m₂.Если второй шар до удара висел неподвижно (ν₂=0) то после удара остановится первый шар (ν₁'=0),а второй будет двигаться с той же скоростью и в том же направлении,в котором двигался первый шар до удара(ν₂'=ν₁);б)m₁>m₂.Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (ν₁'<ν₁). Скорость второго шара после удара больше, чем скорость первого после удара (ν₂'>ν₁') в) m₁<m₂. При ударе направление движения первого шара изменяется - шар отскакивает обратно. При этом второй шар движется в сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. ν₂'<ν₁ г) m₂>>m₁ (например, столкновение шара со стеной) ν₁'= -ν₁; ν₂' ≈ 2m₁ν₂'/m₂.

13. Центральный удар абсолютно неупругих шаров. Расчет скорости шаров после соударения. Соударение двух шаров с резко отличающимися массами Удар двух тел называется абсолютно неупругим, если после удара оба тела движутся как одно единое целое.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает: кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. После такого удара столкнувшиеся тела соединяются воедино и либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполня­ется лишь закон сохранения импульса, закон же сохранения механиче­ской энергии не соблюдается: имеет место закон сохранения суммарной энергии - механической и внутренней. Если массы шаров m₁ и m₂, их скорости до удара ν₁ и ν₂, то, используя закон сохранения импульса

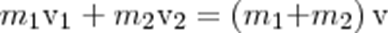
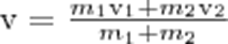 В случае движения шаров навстречу друг другу они вместе будут продолжать движение в ту сторону, в которую двигался шар с большим импульсом. В частном случае, если массы шаров равны (m₁=m₂), то 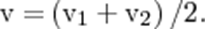Если ударяемое тело было первоначально неподвижно (ν₂=0), то  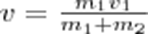Когда m₂>>m₁ (масса неподвижного тела очень велика), то ν<<ν₁ и практически вся кинетическая энергия тела переходит при ударе в другие формы энергии.