Масса. Импульс. Сила. Второй закон Ньютона.

Масса тела – физическая величина, являющаяся одной из основных характеристик материи,определяющая ее инерционные и гравитационные св-ва. Масса тела величина постоянная, не изменяющаяся при его движении; масса-величина действительная-масса составного тела равна массе его частей.

Сила – векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Импульс материальной точки – векторная величина, численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости; количество движения. p=mυ.

Второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). a=F/m или F=ma=mdυ/dt.

Более общая формулировка закона Ньютона – скорость изменения импульса материальной точки равна действующей на неё силе. F=dp/dt.

Силы взаимодействия. Третий закон Ньютона.

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки: F₁₂= - F₂₁, где F₁₂ – сила, действующая на первую материальную точку со стороны второй; F₂₁ – сила, действующая на вторую материальную точку со сторону первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

Третий закон Ньютона позволят осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Третий закон Ньютона справедлив только в инерциальных системах отсчета.

Энергия кинетическая и потенциальная. Полная механическая энергия и закон ее сохранения. Примеры применения законов сохранения энергии.

 Кинетической энергией тела называется энергия его поступательного движения.. Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона: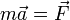

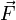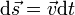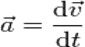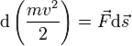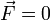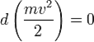— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим: Если система замкнута, то есть , то , а величина 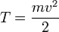остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

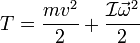
где: 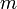— масса тела 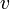— скорость центра масс тела 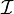— момент инерции тела 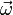— угловая скорость тела.

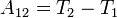
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия определяется с точностью до некоторой постоянной. Это не отражается на физических законах, так как в них входят или разность потенциальных энергий в двух положениях тела, или производная потенциальной энергии по координатам. Поэтому потенциальную энергию тела в каком-то определённом положении считают равной нулю (выбирают нулевой уровень отсчёта), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Работа совершается за счет убыли потенциальной энергии:dA=-dП. Для консервативных сил:

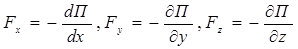.Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела с массой m, поднятого на высоту h поверхностью земли равна П=mgh,Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком: A = –(E_р2 – E_р1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел: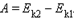

Следовательно 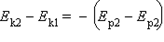или E_k1 + E_p1 = E_k2 + E_p2

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = E_k + E_p называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

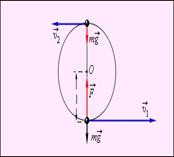Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости Рис поясняет решение этой задачи.

Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде: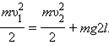

Обратим внимание на то, что сила F натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы. 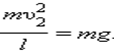, 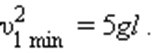. 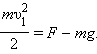Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно

Прочность нити должна, очевидно, превышать это значение.

F = 6mg

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.

12. Центральный удар абсолютно упругих шаров. Расчет скорости шаров после соударения. Соударение двух шаров с резко отличающимися массами. Ударом называется столкновение тел, при котором за весьма короткий промежуток времени происходят значительные изменения скоростей сталкивающихся тел. Удар называется централь­ным, если тела до удара движутся вдоль прямой, проходящей через их центры инерции.Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие виды энер­гии. Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса. Обозначим скорости шаров массами m₁ и m₂ до удара через ν₁ и ν₂, после удара - через ν₁' и ν₂' . Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево. При указанных допущениях законы сохранения имеют вид: 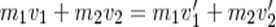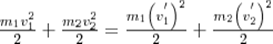Произведя соответствующие преобразования в выражениях,получим 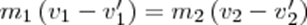(3), 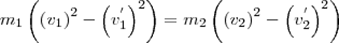откуда 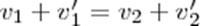(5). Решая уравнения(3)(5)получаем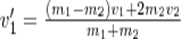 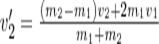.При ν₂=0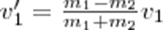  

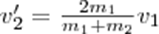
а) m₁=m₂.Если второй шар до удара висел неподвижно (ν₂=0) то после удара остановится первый шар (ν₁'=0),а второй будет двигаться с той же скоростью и в том же направлении,в котором двигался первый шар до удара(ν₂'=ν₁);б)m₁>m₂.Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (ν₁'<ν₁). Скорость второго шара после удара больше, чем скорость первого после удара (ν₂'>ν₁') в) m₁<m₂. При ударе направление движения первого шара изменяется - шар отскакивает обратно. При этом второй шар движется в сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. ν₂'<ν₁ г) m₂>>m₁ (например, столкновение шара со стеной) ν₁'= -ν₁; ν₂' ≈ 2m₁ν₂'/m₂.

13. Центральный удар абсолютно неупругих шаров. Расчет скорости шаров после соударения. Соударение двух шаров с резко отличающимися массами Удар двух тел называется абсолютно неупругим, если после удара оба тела движутся как одно единое целое.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает: кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. После такого удара столкнувшиеся тела соединяются воедино и либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполня­ется лишь закон сохранения импульса, закон же сохранения механиче­ской энергии не соблюдается: имеет место закон сохранения суммарной энергии - механической и внутренней. Если массы шаров m₁ и m₂, их скорости до удара ν₁ и ν₂, то, используя закон сохранения импульса

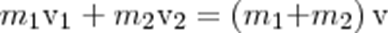
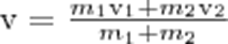 В случае движения шаров навстречу друг другу они вместе будут продолжать движение в ту сторону, в которую двигался шар с большим импульсом. В частном случае, если массы шаров равны (m₁=m₂), то 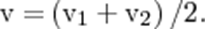Если ударяемое тело было первоначально неподвижно (ν₂=0), то  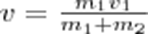Когда m₂>>m₁ (масса неподвижного тела очень велика), то ν<<ν₁ и практически вся кинетическая энергия тела переходит при ударе в другие формы энергии.

Вопрос 46. Образование волн в упругой среде. Продольные и поперечные волны. Уравнение плоской волны. Фазовая скорость. Принцип суперпозиции. Стоячие волны.

Если частицу упругой среды привести в колебательную систему то вследствии упругой связи она вовлечет в это колебательное движение соседнюю частицу. Эти соседние частицы в свою очередь воздействуют на соседние с ними и так далее. и колебания таким образом начнут распространяться в среде. Процесс распространения колебательного движения в среде называется волновым движением или волной. Волны делятся на: 1)продольные; 2)поперечные. Если каждая частица среды колебаний направлена перпендикулярно распространению волны – это поперечные волны. Если каждая частица среды колебаний распространяется в направлении волны то такая волна называется продольной. В поперечных волнах частица среды в направление распространения волны не перемещается. Колебания каждой последующей точки среды запаздывает по фазе относительно колебаний предыдущей точки. Гребни и впадины перемещаются вдоль направления волны. Скорость с которой в среде распространяются одинаковые фазы колебаний называется фазовой скоростью 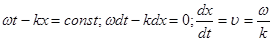. Поверхности образованные точками с одинаковыми фазами называются поверхностями одинаковых фаз или волновыми поверхностями. Если поверхности одинаковых фаз представляют собой плоскости параллельные друг другу то это плоские волны. Уравнение плоской волны:  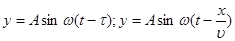- общее уравнение плоской бегущей волны, оно указывает смещение точки среды в момент времени t у которых координата х. 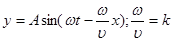- волновое число,тогда 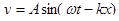.Физический смысл волнового числа: Волновое число показывает сколько одинаковых волн укладывается на отрезке длиной 2пи метра. Если в среде распространяются одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции волн. Принцип суперпозиции утверждает, что движение, вызванное распространением сразу нескольких волн, есть снова некоторый волновой процесс. Таким процессом, например, является звучание оркестра. Оно возникает от одновременного возбуждения звуковых колебаний воздуха отдельными музыкальными инструментами. Замечательно, что при наложении волн могут возникать особые явления. Их называют эффектами сложения или, как еще говорят, суперпозиции волн. Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.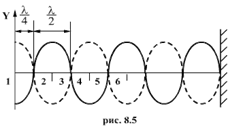

Уравнение стоячей волны можно получить сложением уравнения падающей волны 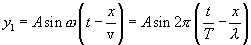и уравнения отраженной волны .

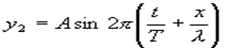Это уравнение стоячей волны определяет смещение любой точки волны.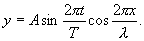

Пространство и время. Механическое движение. Система отсчёта.

Пространство и время, философские категории. Пространство — форма сосуществования материальных объектов и процессов (характеризует структурность и протяженность материальных систем); время — форма и последовательные смены состояний объектов и процессов (характеризует длительность их бытия). Пространство и время имеют объективный характер, неразрывно связаны друг с другом, бесконечны. Универсальные свойства времени — длительность, неповторяемость, необратимость; всеобщие свойства пространства — протяженность, единство прерывности и непрерывности.

Механическое движение – это изменение с течением времени взаимного расположения тел и их частей.

Система отсчета – совокупность системы координат и часов, связанных с телом отсчёта. В декартовой системе координат положение данной точки в данный момент времени по отношению к этой системе характеризуется тремя координатами x , y , z или радиус-вектором r , проведённым из начала системы координат в данную точку. При движении материальной точки её координаты с течением времени изменяются. В общем случае её движение определяется скалярными уравнениями,

x=x(t);

y=y(t); (1.1.)

z=z(t).

 эквивалентными векторному уравнению r=r(t).(1.2.)

2.Кинематика материальной точки. Системы отсчета. Два способа описания движения материальной точки. Скорость и ускорение произвольно движущейся материальной точки как производные радиус вектора(первый способ описания движения).СИСТЕМЫ ОТСЧЕТА. Физика изучает события – явления, происходящие в данном месте и в данное время. Очевидно, что значения координат события x, y, z и момента наступления события t зависят от выбранной системы отсчета. Все физические законы также формулируются относительно некоторой системы отсчета. Под системой отсчета понимают совокупность тела отсчета, координатных осей, измерительного масштаба и часов. В заданной системе отсчета есть принципиальная возможность определить место и время события. Так введенную систему координат называют иначе декартовой системой. Конечно, можно ввести бесконечно много других систем координат, связанных с декартовыми координатами некоторыми преобразованиями, например, цилиндрическую или сферическую системы координат. В классической физике подразумевается, что геометрия трехмерного пространства, описываемого такой системой координат, является евклидовой

Способы описания движения: векторный и координатный.

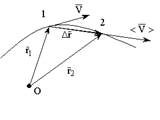Векторный способ. Положение материальной точки задается с помощью радиуса-вектора 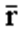относительно некоторой неподвижной точки О. 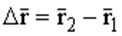- вектор перемещения материальной точки за время 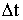. 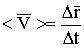- вектор средней скорости. 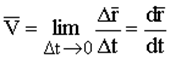- вектор мгновенной скорости.

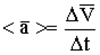- среднее ускорение,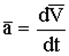

- мгновенное ускорение МТ.