Назначение теста. Сравнение эмпирического распределения N наблюдаемых частот с теоретическим распределением, задаваемым соответствующей функ­цией распределения.

Вычисляются эмпирическая кумулятивная функция распределения (ЭКФР) и теоретическая кумулятивная функция распределения (ТКФР), которые затем дважды сравниваются друг с другом. Вначале определяется разность между текущими значениями обеих функций и находится максимальное положитель­ное значение среди всех полученных (Ď). Затем определяется разность между предыдущим значением ЭКФР и текущим значением ТКФР и находится наи­меньшее отрицательное значение среди всех полученных (D).

Оба значения сравниваются друг с другом по модулю, среди них выбирает­ся набольшее и вычисляется значение Z для статистики Колмогорова — Смирнова:

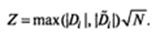
Программный синтаксис (для случая равномерного распределения):

NPAR TEST
/K – S (UNIFORM)= var

/MISSING ANALYSIS.

Тест последовательностей

Назначение теста. Проверка случайного характера последовательности ди­хотомических значений.

Для анализируемой последовательности, образованной дихотомической переменной, принимающей, например, значения 0 и 1, определяется, сколько раз в ней встречаются значение 0 (n₀), значение 1 (n₁) и количество серий r из нулей и единиц (включая единичные значения нулей и единиц).

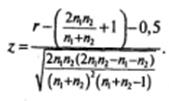
На основании полученных данных о n ₀ , n ₁ и r вычисляется значение z:

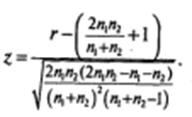
В случае маленькой выборки (менее 50 значений) используются поправки:

1. Если 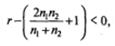 формула принимает вид:

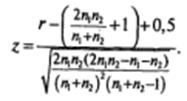
2. Если 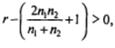  формула принимает вид:

По таблице z-распределения определяется вероятность, соответствующая вычисленному значению z для односторонней критической области.

Программный синтаксис (для дихотомической переменной 0,1):

NPAR TEST

/RUNS (1) = var
/MISSING ANALYSIS.

Биномиальный тест

Назначение теста. Сравнение частоты появления двух дихотомических переменных, имеющих вероятности p и q =(1- р), если после N независимых испытаний частота появления первой из них равна n ₁, частота появления второй из них равна n ₁ (N= n ₁ + n ₂).

Вероятность полученного результата рассчитывается по следующей формуле (формула Бернулли), где

m = min (n₁, n₂):

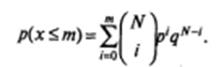
В этом случае, когда N  > 25, возможно применение формулы, связанной с вычислением z:

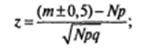
(m + 0,5) используется в том случае, когда х < Np;

(m – 0,5) используется в том случае, когда х > N p.

По таблице z -распределения определяется вероятность, соответствующая вычисленному значению z для односторонней критической области.

Программный синтаксис (для случая р=q=0,5):

NPAR TEST

/BINOMIAL (.50) = var
/MISSING ANALYSIS.