
Упорядочим оценки по ивриту и результаты тестирования в порядке убывания и проранжируем их (табл. 8.10).
Таблица 8.10
Упорядоченные и проранжированные результаты экзамена и тестирования
| Иврит | 93 | 90 | 85 | 83 | 83 | 80 | 77 | 75 | 71 | 67 |
| Ранг | 1 | 2 | 3 | 4,5 | 4,5 | 6 | 7 | 8 | 9 | 10 |
 Логическое мышление Логическое мышление
| 95 | 93 | 90 | 88 | 88 | 80 | 75 | 73 | 69 | 64 |
| Ранг | 1 | 2 | 3 | 4,5 | 4,5 | 6 | 7 | 8 | 9 | 10 |
Заменим в таблице 8.9 результаты в 100-балльной шкале соответствующими рангами. Получим новую таблицу 8.11.
Таблица 8.11
Ранги результатов экзамена по ивриту и тестирования логического мышления
| Иврит (ранги) | 4,5 | 2 | 8 | 6 | 1 | 9 | 4,5 | 10 | 3 | 7 |
| Логическое мышление (ранги) | 1 | 3 | 8 | 4,5 | 2 | 9 | 4,5 | 7 | 10 | 6 |
Упорядочим значения рангов по ивриту от 1 до 10 и соответствующим образом расположим значения рангов для логического мышления (табл. 8.12). Вычислим для каждого ранга во второй строке число совпадений и инверсий.
Таблица 8.12
Упорядоченные ранги результатов экзамена по ивриту и соответствующие ранги
Результатов тестирования
| Иврит (ранги) | 1 | 2 | 3 | 4,5 | 4,5 | 6 | 7 | 8 | 9 | 10 * |
| Логическое мышления (ранги) | 2 | 3 | 10 | 1 | 4,5 | 4,5 | 6 | 8 | 9 | 7 |
| Совпадения | 7 | 6 | 0 | 5 | 4 | 4 | 3 | 1 | 0 | 0 |
| Инверсии | 1 | 1 | 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Обратите внимание! При подсчете совпадений и инверсий связанные ранги учитываются только один раз. Например, правее ранга 2 расположено 8 значений, больших, чем 2; 3; 10; 4,5; 4,5; 6; 8; 9; 7. Но поскольку значения 4,5 и 4,5 образованы связанными рангами, они берутся в расчет только один раз. Поэтому фактическое число совпадений для ранга 2 будет не 8, а 7.
Сумма совпадений = (7 + 6 + 0 + 5 + 4 + 4 + 3 + 1 + 0 + 0) = 30
Сумма инверсий = (1 + 1 + 6 + 0 + 0 + 0 + 0 + 1 + 0 + 0) = 9
S = (Сумма совпадений – Сумма инверсий) = (30 - 9) = 21
При наличии связанных рангов используется иная формула для вычисления коэффициента ранговой корреляции Кендалла τ:
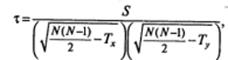
где Тх=0,5∑ tx(tx -1), Ту=0,5∑ tу(tу -1), tx, tу — размер каждой группы связанных
рангов (количество повторяющихся значений) в первой (х) и второй (у) строках.
В табл. 8.12 в первой строке (ранги оценок по ивриту) есть одна группа связанных рангов (4,5 и 4,5). Здесь tx =2 и Тх = 1/2[2(2 -1)] = 1.
Аналогичная ситуация во второй строке — одна группа связанных рангов, включающая два значения: 4,5 и 4,5. Поэтому tу =2 и Ту =1/2[2(2 -1)] = 1.
Подставим все необходимые значения в формулу для вычисления τ:

 Проверим полученные значения коэффициента ранговой корреляции Кендалла на значимость.
Проверим полученные значения коэффициента ранговой корреляции Кендалла на значимость.
Вначале проверим на значимость значение τ для первого примера (ранжирование фотографий): τ =–0,485.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтернативную гипотезы.
Н0: Коэффициент корреляции между результатами оценивания женской привлекательности представителями двух различных культур равен нулю.
Н1: Коэффициент корреляции между результатами оценивания женской привлекательности представителями двух различных культур отличен от нуля (двусторонняя критическая область).
Для проверки коэффициента ранговой корреляции Кендалла на значимость используется несколько подходов, в зависимости от значения N.
Если N > 10, то вначале вычисляется значение z :
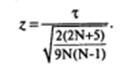
Затем по таблице z-распределения (см. табл. 1, Приложение 2) определяется вероятность (для односторонней критической области), соответствующая полученному значению. Если эта вероятность оказывается больше выбранного уровня значимости а, нет оснований отвергнуть нулевую гипотезу. Если найденная вероятность меньше выбранного уровня значимости α или равна ему, нулевая гипотеза отклоняется и принимается альтернативная.
Вычислим z для τ = –0,485 и N= 12.
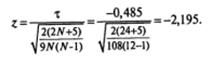
В таблице 1 (Приложение 2) для z -распределения, находим, что значению z = – 2,195 соответствует вероятность р =0,0143.
В том случае, если критическая область двусторонняя (как в нашем случае), значение вероятности необходимо удвоить: р =0,0286.
Поскольку значение уровня значимости α =0,05 больше, чем р =0,0286, нулевая гипотеза отклоняется и принимается альтернативная. Существует значимая, отличная от нуля корреляционная связь между результатами оценивания женской привлекательности представителями двух различных культур.
Проверим на значимость результат, полученный во втором примере (случай связанных рангов): τ = 0,477.
Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.
Н0: Коэффициент корреляции между уровнем знания иврита и показателями логичности мышления у новых иммигрантов равен нулю.
Н1: Коэффициент корреляции между уровнем знания иврита и показателями логичности мышления у новых иммигрантов отличен от нуля (двусторонняя критическая область).
Для случая малых выборок (N ≤ 10) существует специальная таблица, содержащая значения р (односторонняя критическая область) в зависимости значений т и N (см. табл. 12, Приложение 2).
Из таблицы 12 находим, что для τ = 0,477 и N= 10 значение р лежит между р =0,036 (для τ = 0,467) и р =0,023 (для τ = 0,511). Примем р =0,030. Поскольку альтернативная гипотеза сформулирована для случая двусторонней критической области, удваиваем это значение: р =0,060.
Полученное значение вероятности оказалось больше, чем α =0,05. Оснований отвергнуть нулевую гипотезу нет. Коэффициент корреляции между уровнем знания иврита и показателями логичности мышления у новых иммигрантов — выпускников языковых курсов незначимо отличается от нуля9.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Результаты ранжирования фотографий поместим в переменные «Ранг 1» (range 1) и «Ранг 2» (range 2) Дальнейшие действия и получаемый результат показаны на рис. 8.6-8.8.

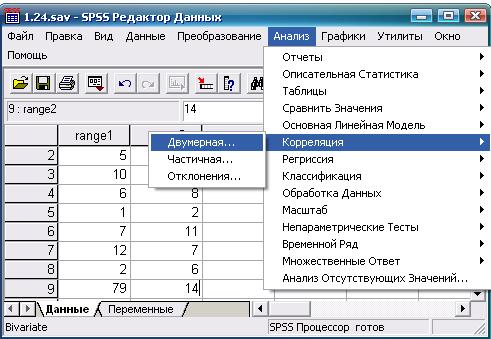
Рис. 8.6. Выбор требуемой статистической процедуры



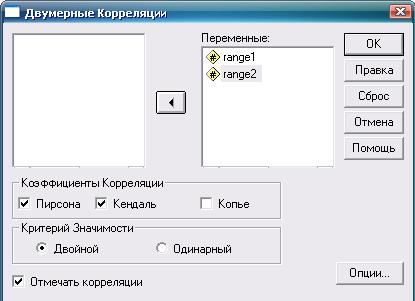
Рис. 8.7. Коэффициент ранговой корреляции Кендалла: необходимые действия и настройки
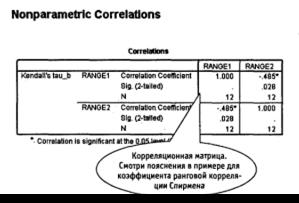
Рис. 8.8. Коэффициент ранговой корреляции Кендалла: результат
Рассмотрим пример со связанными рангами. В переменной «Иврит» (Нebrew) поместим результаты экзамена по ивриту, а в переменной «Логика» (logic) сведения об уровне логического мышления. Результат вычислений для случая двусторонней и односторонней критических областей показан на рис. 8.9.
Обратите внимание! Один и тот же коэффициент корреляции, в зависимости от того, как сформулирована альтернативная гипотеза, в одном случае признается незначимым, а в другом — значимым!
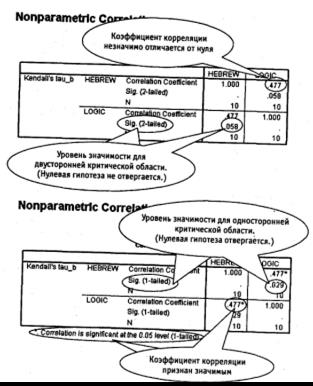
Рис. 8.9. Коэффициент ранговой корреляции Кендалла: результат
(пример для связанных рангов)
Дата: 2018-12-21, просмотров: 694.