Подростки	Причины начала употребления
	1	2	3	4	5	6
A	1	4	2	3	6	5
B	2	1	3	4	5	6
C	3	1	2	5	4	6
D	3	1	2	5	4	6
E	2	3	1	6	4	5
F	1	4	3	2	6	5
G	1	2	3	4	5	6
H	1	3	4	2	6	5
I	2	1	6	4	5	3
J	1	3	4	6	2	5
K	17	23	30	41	47	52	∑Ri=210
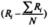
	-18	-12	-5	6	12	17
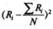
	324	144	25	36	144	289	S=962

1. Для каждого столбца таблицы найдем сумму рангов (R_i), запишем ее вни­зу соответствующего столбца и затем найдем сумму полученных значений (∑ R_i).

2. Определим для каждого столбца значение ( 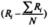) и квадрат этого значения: ( 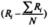)², где N – число ранжируемых объектов (в нашем случае N=6). Полученные результаты также запишем внизу каждого столбца.

3. Найдем сумму значений 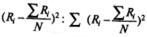 и обозначим ее S.

Коэффициента конкордации Кендалла W вычисляется по следующей формуле:

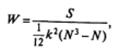
где k — число испытуемых или экспертов (в нашем случае k = 10) . Подставим в формулу все необходимые значения:

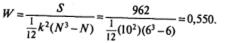
При использовании коэффициента конкордации Кендалла W также возможны случаи связанных рангов, однако мы не будем рассматривать эту си­туацию. Она описана, например, у S. Siegel [Siegel, 1956]. 

Полученный результат требует проверки на значимость. Для этого используется таблица критических знаний для теста Х².

Вначале вычисляется значение Х²:

Х²= k(N–1)W

Затем полученное значение Х²мпир сравнивается с критическим значением Х²_критич. которое находится в таблице 2 (Приложение 2), для числа степеней свободы df =(N -1)                                                                    и выбранного значения уровня значимости α.

Если Х²_эмпир< Х²_критич. нет оснований отвергнуть нулевую гипотезу. Если Х²_эмпир> Х²_критич. нулевая гипотеза отвергается и принимается альтернативная.

Выберем уровень значимости α = 0,05 и сформулируем нулевую и альтернативную гипотезы.

Н₀: Коэффициент конкордации, полученный на основе ранжирования де­сятью испытуемыми шести объектов, равен нулю.

Н₁: Коэффициент конкордации, полученный на основе ранжирования де­сятью испытуемыми шести объектов, больше нуля (односторонняя критическая

¹¹ Поскольку коэффициент конкордации не может быть меньше нуля, двусторонняя критическая область здесь невозможна.      

Определим значение Х²_эмпир:

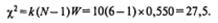
Из табл. 2 находим, что для df =( N -1)= (6—1) = 5 и уровня значимости α =0,05

Х²_критич =11,07.

Поскольку эмпирическое значение больше критического (11,07), нулевая гипотеза отвергается и принимается альтернативная. Коэффициент конкорда­ции Кендалла, полученный на основе ранжирования десятью испытуемыми шести объектов, значимо отличается от нуля.

ВКЛЮЧАЕМ КОМПЬЮТЕР...

Создадим 6 переменных для каждой из причин начала употребления наркотиков: от «Причина 1» (reason 1) до «Причина 6» (reason 6) и укажем, какой ранг им присво­ен каждым из десяти подростков. Дальнейшая последовательность действий и ко­нечный результат показаны на рис. 8.10-8.12.

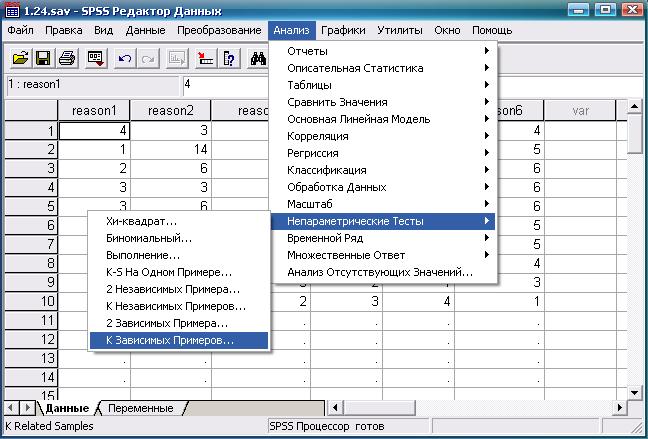
Рис. 8.10. Выбор требуемой статистической процедуры

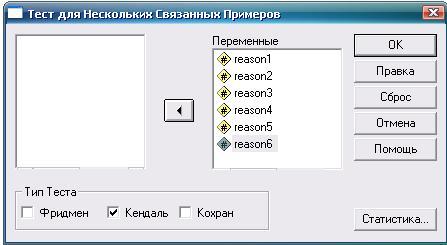
Рис. 8.11. Коэффициент конкордации Кендалла: необходимые действия и настройки

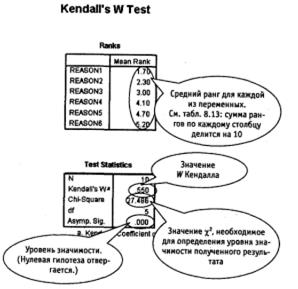
Рис. 8.12. Коэффициент конкордации Кендалла: результат

ПРИЛОЖЕНИЯ

Приложение 1