Процесс подсчета числа совпадений и инверсий покажем на рис. 8.5.

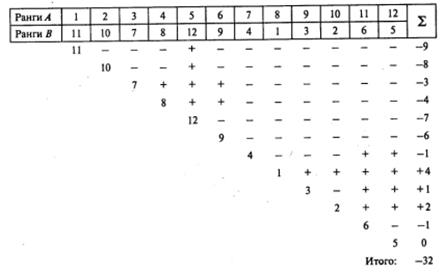
Рис. 8.5. Подсчет суммы совпадений и инверсий рангов

Совпадения означают, что если для первого студента (студент А) числа воз­растают слева направо от 1 до 12, то для второго студента (студент В) эти числа также должны меняться слева направо в сторону возрастания. Инверсии озна­чают, что в то время, как числа для студента А возрастают от 1 до 12, числа для студента В уменьшаются.

Каждое из чисел для студента В будем последовательно сравнивать с осталь­ными числами, которые расположены правее от него. Если правее будет стоять большее число, обозначим это как «+»(совпадение). Если правее будет стоять; меньшее число, обозначим это как «−» (инверсия). В конце каждой строки найдем число совпадений (количество плюсов), число инверсий (количество минусов) и разность между ними (между количеством плюсов и количеством минусов). Затем подсчитаем общую сумму по вертикали, которая будет равна разности между суммой всех совпадений и суммой всех инверсий⁷. Обозначим полученный результат как S:

S = (Сумма всех совпадений — Сумма всех инверсий).

⁷ Нетрудно видеть, что это соответствует разности между количеством всех «плюсов» (17) и количеством всех «минусов» (49) на рис. 8.5: S= 17 − 49= −32.

Вычислим значение коэффициента ранговой корреляции Кендалла τ («тау»; Кендалла) по формуле:

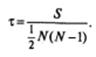
Для нашего случая S = − 32; N=12.

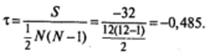
Существует несколько модификаций формулы для вычисления коэффи­циента ранговой корреляции Кендалла τ, в которых используется либо значе­ние числа совпадений, либо значение числа инверсий, либо (как в нашем случае) как совпадения, так и инверсии. Разумеется, все они дают одинаковый результат.

На основании рассмотренного примера можно видеть, что вычисление коэффициента ранговой корреляции Кендалла носит более простой характер по сравнению с вычислением коэффициента ранговой корреляции Спирмена. Однако это справедливо только для небольших выборок. В случае возрастания значения N заметно увеличивается объем вычислений (подсчет числа совпаде­ний и инверсий) и, соответственно, возрастают затраты времени на вычисление корреляции по Кендаллу⁸.

⁸ У корреляции по Кендаллу есть ряд других, более существенных достоинств, например простота интерпретации полученного результата. Так, в частности, можно показать, что для двух ранговых рядов вероятность совпадений равна (1+ τ) / 2, а вероятность инверсий равна (1 − τ)/2. Например, если τ =0,6, то это означает 80% совпадений и 20% инверсий. Иными словами, если два студента, оценивающие женскую привлекательность, получили τ =0,6, то это означает, что их мнения относительно женской привлекательности совпадают в четыре раза чаще, чем не сов­падают. Интерпретация коэффициентов корреляции по Пирсону или Спирмену носит не столь явный характер. Полученный результат надо вначале возвести в квадрат, а затем сделать малопо­нятный неспециалисту вывод относительно доли дисперсии, которая может быть объяснена полученным результатом.

Для корреляции по Кендаллу также существует проблема связанных рангов. Кроме этого, здесь используется иной подход к проверке значимости получае­мых результатов.

Рассмотрим вначале ситуацию со связанными рангами.

Проверялась гипотеза о том, что успехи в изучении иврита новыми имми­грантами связаны с уровнем развития их логического мышления, позволяю­щего понять и использовать внутреннюю логику этого языка. Десять добро­вольцев из числа новых иммигрантов, которые завершили стандартный курс обучения ивриту и сдали по нему экзамен, были протестированы с использо­ванием методик, оценивающих логическое мышление. В таблице 8.9 приведе­ны результаты экзамена по ивриту и результаты тестирования (все в 100-балль­ной шкале).

Таблица 8.9